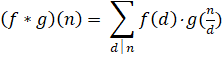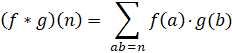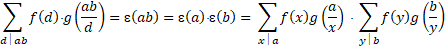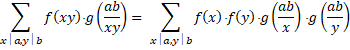Dirichlet convolutie, Mobius functie

© h.hofstede (h.hofstede@hogeland.nl)

Dirichlet-convolutie.

Direct maar de definitie:

Voor twee arithmetische functies f en g is het Dirichlet-convolutieproduct f * g gedefinieerd als:

In woorden: je loopt alle delers van n af, past steeds functie f op de deler toe en vermenigvuldigt dat met g toegepast op het quotiënt van die deler. Die producten tel je allemaal bij elkaar op. Simpeler genoteerd:

Neem bijvoorbeeld f(n) = n² en g(n) = n,
Dan is (f * g)(12) = 1² • 12 + 2² • 6 + 3² • 4 + 4² • 3 + 6² • 2 + 12² • 1 = 3792

Het lijkt een beetje een vergezochte constructie, maar geloof me, je kunt er verrassende dingen op een eenvoudige manier mee bewijzen. Eerst maar een paar naamgevingen en eigenschappen.

Een arithmetische functie is inverteerbaar als er een functie g bestaat zodat f * g = ε.
Daarbij is de functie ε gedefinieerd als:

Die g wordt dan de Dirichlet-inverse van f genoemd (vaak genoteerd als f^-1 ).
Die ε is een soort eenheidselement wat convoluties betreft.
Er geldt altijd ε * f = f * ε = f. (waarbij 𝕀 de identiteit is: 𝕀(n) = n)

Stelling 1 : f is inverteerbaar ⇔ f(1) ≠ 0
Bewijs.

⇒

f(1) • f^-1(1) = (f * f ^-1)(1) = ε (1) = 1 dus f(1) ≠ 0 want dan zou er 0 uitkomen.

⇐

f(1) • g(1) = 1 dus daaruit is g(1) te berekenen.
f(1) • g(2) + f(2) • g(1) = 0 dan is daaruit g(2) te berekenen want de rest is bekend.
f(1) • g(3) + f(3) • g(1) = 0 dan is daaruit g(2) te berekenen want de rest is bekend.
f(1) • g(4) + f(2) • g(2) + f(4) • g(1) = 0 dan is daaruit g(2) te berekenen want de rest is bekend.
enz.
Daarmee is g uniek bepaald.
En passant hebben we meteen aangetoond dat er bij elke f slechts één inverse g bestaat.

q.e.d.

Stelling 2 : Als f en g multiplicatief zijn, dan is f * g ook multiplicatief.
Bewijs:

Stel a = p₁ • p₂ • p₃ .... en b = q₁ • q₂ • q₃...   waarbij geen enkele p gelijk is aan een q (a en b zijn copriem).
(f * g)(a) = Σ f(deel p) • g(rest p)
(f * g)(b) = Σ f(deel q) • g(rest q)
dus (f * g)(a) • (f * g)(b) = Σ f(deel p) • g(rest p) • Σf(deel q) • g(rest q)     .......(1)

ab = p₁ • p₂ • p₃ ....• q₁ • q₂ • q₃...
(f * g)(ab) = Σ f(deel pq) • g(rest pq)
= Σ f(deel p) • f(deel q) • g(rest p) • g(rest q)   .....(2) dat mag omdat f en g beiden multiplicatief zijn.

Zijn (1) en (2) gelijk?
Ja, want in beiden staan precies alle mogelijkheden om uit de rij p₁ • p₂ • p₃ ....q₁ • q₂ • q₃...   een willekeurig aantal p's en q's te kiezen en dan f(deel p) • g(rest p) • f(deel q) • g(rest q) te berekenen.

q.e.d.

Stelling 3 : Als f multiplicatief is, dan is f inverteerbaar, en dan is ook f^-1 multiplicatief.
Bewijs:

Die eerste is een makkie: als f multiplicatief is, dan is f(1) = 1 (immers f(a) = f(1 • a) = f(1) • f(a))
dus is f volgens stelling 1 hierboven inverteerbaar.

Nu nog even dat f^-1 multiplicatief is....
Gebruik volledige inductie voor het product ab.
Stel dat g = f^-1 dan moeten we dus aantonen dat g(ab) = g(a) • g(b)
als ab = 1 dan moet wel gelden a = 1 en b = 1, dus is g(a) = g(b) = g(ab) = g(1) = ¹/_f(1) = 1

Stel dat de stelling geldt tot bepaalde ab, en dat ggd(a, b) = 1....

Maar omdat ggd(a, b) = 1 zijn al die d's in het linkerlid te schrijven als d = xy waarbij x een deler van a is en y een deler van b (eventueel gelijk aan 1). En dan is ggd(x, y) = 1
In plaats van de som over al die delers d te nemen kun je dus net zo goed de som over alle delers xy nemen, met x alle delers van a en y alle delers van b. Dan staat er:

Alleen voor x = y = 1 staat daar rechts onder het somteken f(1) • f(1) • g(ab) • g(ab), in alle andere gevallen heb je te maken met een g van iets dat kleiner is dan ab.
Maar we hadden aangenomen dat voor al die waarden kleiner dan ab geldt dat g multiplicatief is.
Laten we daarom het geval x = y = 1 links eruit halen, dat geeft:

Dus die ene g(ab) is gelijk aan de term rechts voor x = y = 1
Dat geeft g(ab) = f(1) • f(1) • g(a) • g(b) = g(a) • g(b)

q.e.d.

Möbius- functie.

Een getal noemen we kwadraatvrij als geen enkel priemgetal uit de priemfactorontbinding met macht hoger dan 1 voorkomt.
Met dit begrip kunnen we de Möbius-functie μ(n) definiëren:

Kortom: bij allemaal verschillende priemfactoren zegt de Möbiusfunctie of dat een even aantal of een oneven aantal is. Bij dubbele priemgetallen is de Möbiusfunctie altijd direct nul.
Je ziet dus al meteen dat μ(p) = -1 als p een priemgetal is, en dat μ(1) = 1

Stelling: μ(n) is multiplicatief
Bewijs:

Neem twee getallen a en b die geen priemfactor gemeenschappelijk hebben.
Stel a = p₁ • p₂ • p₃ • ..... en b = q₁ • q₂ • q₃ • ....
Zodra één van beiden een dubbele priemfactor heeft, heeft ab die ook, dus is μ(ab) = 0, en dat is dan inderdaad gelijk aan μ(a) • μ(b) want van die beiden is dan minstens één nul.

Neem nu aan dat alle p en q verschillend zijn.
Voor de aantallen p en q zijn er vier mogelijkheden:
(even p, even q). Dan is μ(a) = 1 en μ(b) = 1. ab heeft een even aantal priemfactoren dus μ(ab) = 1
(even p, oneven q). Dan is μ(a) = 1 en μ(b) = -1. ab heeft een oneven aantal priemfactoren dus μ(ab) = -1
(oneven p, even q). Dan is μ(a) = -1 en μ(b) = 1. ab heeft een oneven aantal priemfactoren dus μ(ab) = -1
(oneven p, oneven q). Dan is μ(a) = -1 en μ(b) = -1. ab heeft een even aantal priemfactoren dus μ(ab) = 1
In alle gevallen is μ(ab) = μ(a) • μ(b)

q.e.d.

Stelling: μ * 𝟙 = ε (waarbij 𝟙 de functie is die overal 1 is).
Bewijs:

Omdat μ en 𝟙 beiden multiplicatief zijn, is ook μ * 𝟙 multiplicatief, dus we hoeven de stelling alleen te bewijzen voor de machten van priemgetallen.

Maar ook ε(pⁿ) = 0.

q.e.d.

Dat betekent dat de Möbiusfunctie de inverse is van de functie 𝟙 bij Dirichlet-convolutie.

Gevolg hiervan is, dat de som van μ(d) over alle delers van een getal n altijd gelijk is aan nul.
Voorbeeld.
Neem n = 20 dan zijn de delers van n de getallen 1, 2, 4, 5, 10, 20.
De Möbiusfunctie geeft voor deze zes delers respectievelijk: μ = 1, -1, 0, -1, 1, 0 en dat is samen inderdaad nul.
Oh ja: de enige uitzondering is het getal n = 1: die geeft som 1.

Stelling: De Möbiusinversiestelling: f = μ * g ⇔ g = 𝟙 * f
Bewijs:

⇒

Als f = μ * g dan is 𝟙 * f = 𝟙 * (μ * g) = (𝟙 * μ) * g = ε • g = g

⇐

Als g = 𝟙 * f dan is μ * g = μ * (𝟙 * f ) = (μ * 𝟙) * f = ε • f = f

q.e.d.

Liouville-functie.

Nog een erg beroemde arithmetische functie is de Liouville-functie λ(n) en die is zó gedefinieerd:

λ(n) = (-1)^Ω(n)

Daarbij is Ω(n) het aantal priemfactoren van n. De Liouville-functie zou je kunnen omschrijven als de "pariteit van het aantal priemfactoren". λ(n) heeft maar twee uitkomsten: 1 (even aantal priemfactoren) of -1 (oneven aantal priemfactoren).
De functie (λ * 𝟙)(n) geeft de waarde 1 als n een kwadraat is, en anders 0. (ga dat maar na). Deze functie wordt daarom ook wel een indicatorfunctie voor de kwadraten genoemd.

Toepassingen.

Stelling: 𝟙 * j = 𝕀
Bewijs:

Tel alle breuken {¹/_n, ²/_n, ..., ⁿ/_n} op twee manieren:

•

aan de noemers kun je zien dat dat er n zijn.

•

als je ze allemaal eerst vereenvoudigt, dan heeft elke breuk als noemer een deler d van n de teller is in dat geval niet groter dan d en relatief priem met d, dus dat zijn j(d) breuken.
Het aantal breuken is dan de som over d van j(d)

Daar staat precies de stelling.

q.e.d.

In woorden: "Als je van alle delers d van een getal n telt hoeveel van de getallen tot en met d copriem zijn met d, dan is dat samen evenveel als het getal n zelf".
Voorbeeld: neem het getal 24.
delers: 1, 2, 3, 4, 6, 8, 12, 24
kleinere priemgetallen respectievelijk: 1, 1, 2, 2, 2, 4, 4, 8 en dat is samen....... 24!!!!!!!

Leuke bijkomstigheid: als 𝟙 * j = I dan is j = I * μ (volgt uit de Möbius-inversiestelling hierboven).

Hier zijn een paar verbanden tussen de verschillende arithmetische functies met de Dirichlet-convolutie. Sommigen hebben we al gevonden, anderen zou je zelf kunnen bewijzen.

𝟙 * j = 𝕀
j = μ * 𝕀
μ * 𝟙 = ε
𝟙 * 𝟙 = t
𝕀 * 𝟙 = σ
σ * j = 𝕀 * 𝕀
λ * |μ| = ε
𝟙 = t * μ
t * j = σ

Voorbeeldbewijsje van de laatste:

𝟙 * j = 𝕀
𝟙 * (𝟙 * j) = 𝟙 * 𝕀
(𝟙 * 𝟙) * j = σ
t * j = σ

q.e.d.