Nieuwe pagina 1

De inhoud van een piramide.

© h.hofstede (h.hofstede@hogeland.nl)

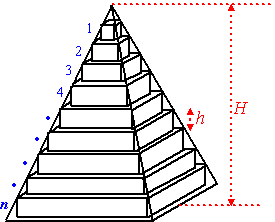
Neem een grote piramide (met oppervlakte grondvlak G, en hoogte H) Laten we hem van blokken bouwen, zoals de Egyptenaren ook ooit deden. Dat zie je hiernaast. We nemen alle lagen even hoog (hoogte h), en nummeren ze van boven naar beneden 1, 2, ..., n.

Je zult wel inzien dat, hoe groter we n nemen, des te nauwkeuriger we de werkelijke inhoud van de piramide krijgen. Immers met kleinere blokjes "past" het er beter in en blijft er steeds minder lege ruimte over.

Stel dat we n lagen hebben gemaakt, dan is de hoogte van elke laag gelijk aan h = ^H/_n
Noem het grondvlak van laag nummer i gelijk aan G_i.
Dan geldt voor de inhoud van laag i: I_i = G_i • ^H/_n

Alle lagen samen hebben dan een inhoud: I_tot = G₁ • h + G₂ • h + G₃ • h + ... + G_n • h
Dat geeft I_tot = h• (G₁+ G₂ + G₃ + ... + G_n)

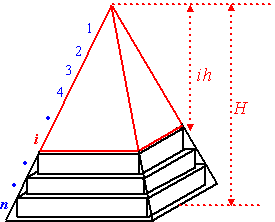
Neem de piramide nummer i met, die hiernaast rood is getekend.
Die piramide is gelijkvormig met de totale piramide (zelfde hoeken).
De verkleiningsfactor (k) van de rode piramide ten opzichte van de totale piramide kun je uit de verhouding van de hoogtes halen:
k = ih/H.
Dan geldt voor de grondvlakken een verhouding k²

Vul dat in in de formule voor de totale inhoud:

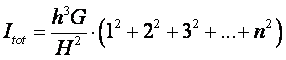Maar h = ^H/_n dus dat geeft:

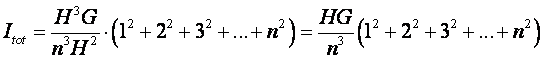Nu is het tijd om een formule voor 1² +2² +3² + ... + n² op te stellen. Daar besteden we een nieuwe paragraaf aan.

Hoe groot is 1² + 2² + 3² + ... + n² ??

Dat kun je met een trucje ontdekken. Bekijk daarvoor de som van een aantal derdemachten.
Er geldt:

De eerste term valt weg tegen de vijfde
De tweede en de derde term aan de linkerkant zijn oude bekenden.

Invullen en de som van i² alleen zetten geeft:

En nu terug naar de piramide.

We waren gebleven bij een formule voor I_tot, en daar kunnen we nu de gevonden som van i²in substitueren:

Als je nu n naar een oneindig groot getal laat gaan (de piramide in steeds meer steeds kleinere blokjes verdelen) dan nadert deze waarde naar ¹/₃GH (die andere twee termen gaan naar nul)

qed.