© h.hofstede (h.hofstede@hogeland.nl)

Nóg een bewijs!
     

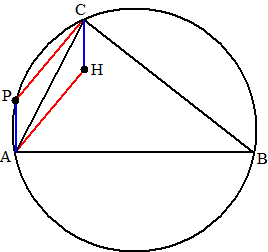
Teken een driehoek ABC met zijn omgeschreven cirkel.
Lijnstuk AP staat loodrecht op AB en snijdt de cirkel in P.
H is het snijpunt van de hoogtelijnen van de driehoek.
BAPC is een koordenvierhoek dus de overstaande hoeken zijn samen 180º.

Omdat ∠BAP = 90º  is dus ook ∠BCP = 90º
Omdat AH hoogtelijn is staat AH ook loodrecht op BC, dus zijn AH en PC evenwijdig  (F-hoeken)

Op dezelfde manier zijn ook CH en AP evenwijdig (beiden loodrecht op AB)
       
Kortom;  AHCP is een parallellogram.
Omdat de overstaande zijden van een parallellogram even lang zijn geldt dus  AP = CH    .....(1)
       
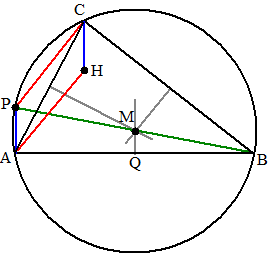
Omdat ∠BAP = 90º  is BP de middellijn van een cirkel door B, A en P  (Thales).
Dat is ook de cirkel door ABC, dus M is het snijpunt van de middelloodlijnen van driehoek ABC. 

De driehoeken BQM en BAP zijn gelijkvormig  (HH) met factor 2  (want BA = 2 • QB omdat MQ middelloodlijn is)

Maar omdat CH = AP  (1)  is dus ook CH = 2 • MQ.
 

       
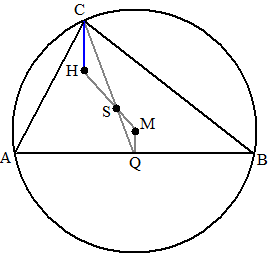
Hiernaast zijn dan de driehoeken CHS en  QMS gelijkvormig (immers CH // MQ)  met factor 2.

Dus CS : SQ = 2 : 1

Maar omdat CQ zwaartelijn is,  is S het zwaartepunt van driehoek ABC!!!

       

© h.hofstede (h.hofstede@hogeland.nl)