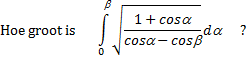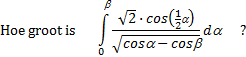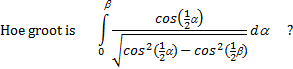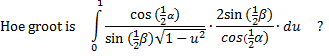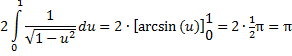© h.hofstede (h.hofstede@hogeland.nl)

     
cos2α = 2cos2α - 1  dus   2cos2α =  1 + cos2α
schakel over van α op 1/2α  dan vind je   2cos2(1/2α) = 1 + cosα       ......(1)
dus  √2cos(1/2α) = √(1 + cosα)
Daarmee is de teller veranderd, en hebben we de tussenstand:  
       

       
(1)  geeft    cosα =  2cos2(1/2α) - 1   en ook   cosβ =  2cos2(1/2β) - 1
Dan wordt de noemer: 
√( 2cos2(1/2α) - 1 - 2cos2(1/2β) + 1)
= √(2cos2(1/2α) - 2cos2(1/2β))
= √2 • √(cos2(1/2α) - cos2(1/2β))
Dat geeft de volgende tussenstand (die √2-factoren vallen tegen elkaar weg):
       

       
We gaan nu een substitutie toepassen.  Altijd leuk.
Neem  u = sin(0,5α)/sin(0,5β)
• Dan is sin(1/2α) = u • sin(1/2β)
Dus is  cos2(1/2α) = 1 - sin2(1/2α) = 1 - u2 sin2(1/2β)   en die gaan we in de noemer vervangen, en dan schrijven meteen ook  cos21/2β  als  1 - sin21/2β.
• Verder is  du = 1/2 • cos(0,5α)/sin(0,5β) • dα   dus  dα =  du • 2sin(0,5β)/cos(0,5α)
• de grenzen  0 en β  veranderen in 0 en 1.
Op naar de volgende tussenstand:

       
Daar valt van alles weg, en we houden een bekende integraal over:
       

       
       

© h.hofstede (h.hofstede@hogeland.nl)