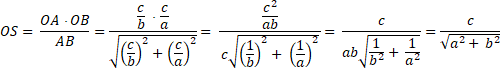afstandsformule punt tot lijn

© h.hofstede (h.hofstede@hogeland.nl)

De afstand van een punt tot een lijn.

In deze les gaan we een formule afleiden voor de afstand van een punt P toto een lijn l.

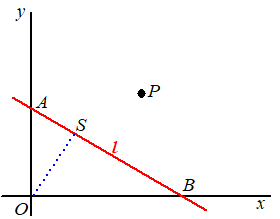
Neem een lijn l: ax + by = c en een punt P(x_P, y_P).
We gaan nu eerst de afstand van de oorsprong tot lijn l berekenen.
Zie de figuur hiernaast.

punt A: x = 0 dus by = c en y = ^c/_b
punt B: y = 0 dus ax = c en x = ^c/_a

Met Pythagoras: AB = √((^c/_b)² + (^c/_a)²)

In driehoek OSA geldt ¹/₂ • OS • AB = ¹/₂ • OA • OB want beiden zijn de oppervlakte van de driehoek.

Dat geeft:

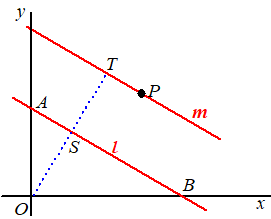
Teken nu de lijn m door punt P evenwijdig aan l.

m is de lijn ax + by = q, en omdat P(x_P, y_P) daar op moet liggen is het de lijn ax + by = ax_P + by_PDan kunnen we afstand OT van de oorsprong toto m direct opschrijven: vervang in de formule voor OS gewoon c door
ax_P + by_P:

De afstand van P tot l is ST en dat is OT - OS:

Daarmee hebben we een algemene formule gevonden voor de afstand van een punt P tot een lijn l. Nog één detail: als die teller negatief is, moet je hem wel positief maken (een afstand kan immers niet negatief zijn) en dat kan door er absolute-waarde strepen omheen te zetten.
Slotresultaat:

Voor de afstand van punt P(x_P, y_P) tot de lijn l: ax + by = c geldt:

Voorbeeld: Bereken de afstand van punt P(3, 6) tot lijn l: 4x + 3y = 14

Sorry, ik kan er ook niet meer van maken......

Nou, dan komen er nu nog een hele zooi toepassingen......

Toepassing 1: Bissectrice.

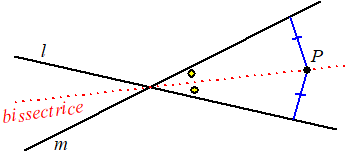
Deze afstandsformule kunnen we nu handig gebruiken om de bissectrice van twee gegeven lijnen op te stellen. Immers, de bissectrice van twee lijnen is de verzameling van alle punten die gelijke afstanden tot beide lijnen hebben.
Dus om zo'n bissectrice te vinden kies je een punt (x, y) en daarvoor stel je de afstand tot de ene lijn gelijk aan de afstand tot de andere.

Voorbeeld.
Stel l is de lijn 3x + 4y = 12 en m is de lijn 5x - 12y = 20
Voor een punt (x, y) van de bissectrice geldt dan:

kruislings vermenigvuldigen: 13 • |3x + 4y - 12| = 5 • |5x - 12y - 20|
Door die absolute-waarde strepen staan daar eigenlijk twee vergelijkingen, die een minteken van elkaar verschillen.
En dat moet natuurlijk ook, immers er zijn twee bissectrices; die rode lijn hierboven maar ook nog de lijn daar loodrecht op: die deelt de anderte hoeken tussen l en m doormidden. Gelukkig maar dat we twee vergelijkingen vinden!!

vergelijking 1: 13(3x + 4y - 12) = 5(5x - 12y - 20)
39x + 52y - 156 = 25x - 60y - 100
14x + 112y = 56 en dat is de eerste bissectrice.

vergelijking 2: 13(3x + 4y - 12) = -5(5x - 12y - 20)
39x + 52y - 156 = -25x + 60y + 100
64x - 12y = 256 en dat is de tweede bissectrice.

Toepassing 2:
Lijn op afstand van een gegeven punt.

Voorbeeld: Geef vergelijkingen van de lijn door (2,3) die afstand 4 tot punt P(3, 8) heeft.
Stel de lijn y = ax + b.
Als die door (2, 3) gaat dan geldt 3 = 2a + b ofwel b = 3 - 2a
De lijn is dus l: y = ax + 3 - 2a ofwel ax - y + 3 - 2a = 0
Invullen in de afstandsformule, met P(3, 8):

eerste vergelijking: 3a - 8 + 3 - 2a = √(a² + 1)
a - 5 = √(a² + 1)
a² - 10a + 25 = a² + 1
10a = 24
a = 2,4 en dat geeft de lijn y = 2,4x - 1,8

De vergelijking met het minteken geeft (omdat we alles kwadrateren) dezelfde oplossing.

Toepassing 3:
Raaklijn door een punt buiten een cirkel.

Voorbeeld: Geef de vergelijking van de raaklijn aan de cirkel (x - 2)² + y² = 18 die door P(-4, 12) gaat.
Stel de lijn y = ax + b
Als die door (-4, 12) gaat dan geldt 12 = -4a + b ofwel b = 12 + 4a
De lijn is dus y = ax + 12 + 4a ofwel ax - y + 12 + 4a = 0
Invullen in de afstandsformule met M(2, 0) en afstand √18:

eerste vergelijking: 6a + 12 = √(18a² + 18)
36a² + 144a + 144 = 18a² + 18
18a² + 144a + 126 = 0
a = -1 ∨ a = -7
Dat geeft de raaklijnen y = -x + 8 en y = -7x - 16

De vergelijking met het minteken geeft wederom dezelfde twee oplossingen.

Toepassing 4:
Gemeenschappelijke raaklijn van twee cirkels.

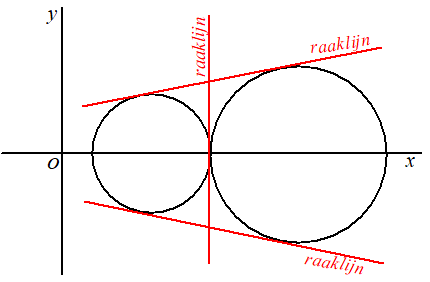
Voorbeeld: De cirkels (x - 3)²+ y² = 4 en (x - 8)² + y² = 9 hebben, behalve de lijn x = 5 nog twee gemeenschappelijke raaklijnen. Geef de vergelijkingen daarvan.

Stel de lijn y = ax + b ofwel ax - y + b = 0
De middelpunten zijn (3, 0) met straal 2 en (8, 0) met straal 3
Dat geeft de volgende twee afstandsformules voor een punt van de lijn tot die middelpunten:

De eerste geeft √(a² + 1) = 0,5 • |3a + b| en dat kun je invullen in de tweede:
|8a + b| = 1,5 • |3a + b|

eerste vergelijking: 8a + b = 1,5(3a + b) en dat geeft b = 7a
invullen in bijv. de eerste vergelijking geeft dan 10a = 2 • √(a² + 1)
100a² = 4a² + 4 geeft a = ±¹/₁₂√6 en dan is b = 7a = ±⁷/₁₂√6

OPGAVEN

Gegeven zijn de lijn

en het punt P (0, 6).

Bereken de afstand van punt P tot lijn l .

Welke twee lijnen door de oorsprong hebben afstand 4 tot punt P ?

c is de cirkel (x - 4)² + (y - 2)² = 4.
Er zijn twee lijnen door punt P die cirkel c raken.

Geef de vergelijkingen van die twee lijnen.