HOUSE BILL NO. 246

"A bill for an act introducing a new mathematical truth and offered as a contribution to education to be used only by the State of Indiana free of cost by paying any royalties whatever on the same, provided it is accepted and adopted by the official action of the legislature of 1897.

"Section 1. Be it enacted by the General Assembly of the State of Indiana: It has been found that a circular area is to the square on a line equal to the quadrant of the circumference, as the area of an equilateral rectangle is to the square on one side. The diameter employed as the linear unit according to the present rule in computing the circle's area is entirely wrong, as it represents the circles area one and one-fifths times the area of a square whose perimeter is equal to the circumference of the circle. This is because one-fifth of the diameter fils to be represented four times in the circle's circumference. For example: if we multiply the perimeter of a square by one-fourth of any line one-fifth greater than one side, we can, in like manner make the square's area to appear one fifth greater than the fact, as is done by taking the diameter for the linear unit instead of the quadrant of the circle's circumference.

"Section 2. It is impossible to compute the area of a circle on the diameter as the linear unit without trespassing upon the area outside the circle to the extent of including one-fifth more area than is contained within the circle's circumference, because the square on the diameter produces the side of a square which equals nine when the arc of ninety degrees equals eight. By taking the quadrant of the circle's circumference for the linear unit, we fulfill the requirements of both quadrature and rectification of the circle's circumference. Furthermore, it has revealed the ratio of the chord and arc of ninety degrees, which is as seven to eight, and also the ratio of the diagonal and one side of a square which is as ten to seven, disclosing the fourth important fact, that the ratio of the diameter and circumference is as five-fourths to four; and because of these facts and the further fact that the rule in present use fails to work both ways mathematically, it should be discarded as wholly wanting and misleading in its practical applications.

"Section 3. In further proof of the value of the author's proposed contribution to education, and offered as a gift to the State of Indiana, is the fact of his solutions of the trisection of the angle, duplication of the cube and quadrature having been already accepted as contributions to science by the American Mathematical Monthly, the leading exponent of mathematical thought in this country. And be it remembered that these noted problems had been long since given up by scientific bodies as unsolvable mysteries and above man's ability to comprehend."

 

LEGISLATIVE HISTORY Introduced IN THE HOUSE Read first time January 18th, 1897  Referred to Committee on Canals Reported and referred to Committee on Education January 19th, 1897 Reported back February 2nd, 1897 Read second time February 5th, 1897 Ordered engrossed February 5th, 1897 Read third time February 5th, 1897 Passed February 5th, 1897 Ayes - 67 - Noes -0-  Introduced by Record  IN THE SENATE  Read first time and referred to committee on Temperance, February 11th, 1897 Reported favorable February 12th, 1897 Read second time and indefinitely postponed February 12, 1897

Niet alleen probeerde Goodman de verkeerde waarde voor p te introduceren; deze "wetenschapper"  had waarschijnlijk zelf niet eens door dat hij ook verschillende waarden voor p beoogde.
Ik citeer uit de tekst hierboven:

Met "equilateral rectangle" wordt natuurlijk gewoon een vierkant bedoeld. Dan staat hier in normale taal:

ofwel

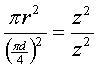
en daaruit volgt gemakkelijk  p = 4

Het volgende citaat uit dezelfde tekst:

Daar staat dus  p = ¹/₅ • (oppervlakte van het vierkant waarvan de omtrek hetzelfde is als van de cirkel)

Dat geeft:

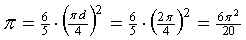en daaruit volgt  p = ²⁰/₆ = ¹⁰/₃ » 3,333

Op naar de volgende:

Hier staat eigenlijk:

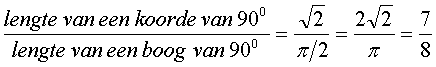en daaruit volgt  p » 3,23

Daaruit volgt en passant dat ^Ö2/₁ = ¹⁰/₇  ofwel  Ö2 » 1,43

daar staat dus  ^2r/_2pr = ^1,25/₄  Þ  p » 3,2