Neem de volgende meetkundige
rij: x, x2, x3,
x4, ...
Voor de som van die rij kunnen we de formule opstellen:
Als we deze uitdrukking differentiëren en daarna met x
vermenigvuldigen krijgen we:
Nog een paar keer hetzelfde doen (differentiëren en met x
vermenigvuldigen) geeft de volgende serie formules: |
|
|
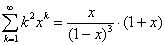
|
|
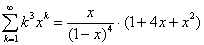
|
|
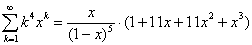
|
|
|
|
De coëfficiënten van de polynomen heten Euler-getallen.
Hier is een lijst: |
|
|
| n |
Euler-getallen |
| 1 |
1 |
|
|
|
|
|
|
|
|
| 2 |
1 |
1 |
|
|
|
|
|
|
|
| 3 |
1 |
4 |
1 |
|
|
|
|
|
|
| 4 |
1 |
11 |
11 |
1 |
|
|
|
|
|
| 5 |
1 |
26 |
66 |
26 |
1 |
|
|
|
|
| 6 |
1 |
57 |
302 |
302 |
57 |
1 |
|
|
|
| 7 |
1 |
120 |
1191 |
2416 |
1191 |
120 |
1 |
|
|
| 8 |
1 |
247 |
4293 |
15619 |
15619 |
4293 |
247 |
1 |
|
| 9 |
1 |
502 |
14608 |
88234 |
156190 |
88234 |
14608 |
502 |
1 |
|
|
|
De som van elke rij is gelijk aan n!
Lijkt wel wat op de driehoek van Pascal, vind je niet?
Als je ze op die manier rangschikt geldt de
recursievergelijking E(n,m) = m •
E(n - 1, m) + n • E(n, m -
1) |
|
|
| Toepassingen |
|
|
|
Er zijn veel toepassingen in de
combinatoriek.
Bijvoorbeeld: het mde Euler-getal in rij n
stelt het aantal permutaties van n elementen met
precies m verhogingen.
Raadseltje d'r bij dan maar?
Je hebt een doos met 8 ballen, genummerd 1 tm 8, en gaat ze er
één voor één uithalen.
Zodra een bal een hoger nummer heeft dan degene er vlak voor
krijg ik die lagere.
Hoe groot is de kans dat ik na afloop 4 ballen zal hebben?
Oplossing
In totaal zijn er 8! = 40326 volgorden.
Het aantal manieren met 4 verhogingen is 15619 (tabel)
De kans is dus 15619/40326 = 38,7% |
|
|
|
|
|