| Op weg naar het einde... |
|
|
Voor het uiteindelijke bewijs zijn
twee begrippen essentieel. Het eerste is "Onvermijdelijke
Verzameling" ('unavoidable set') het tweede "Verkleinbare
Kaart" ('reducible configuration').
Wat houdt het in? |
|
|
| 1. Onvermijdelijke
Verzameling |
|
|
|
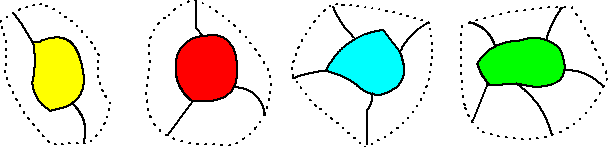
Eerder zagen we al dat een kaart
altijd minstens één land heeft dat vijf of minder buren heeft
("vijfburenstelling").
Dat betekent dat van de volgende verzameling er altijd minstens
ééntje op een kaart aanwezig is: |
|
|
 |
|
|
We zagen al dat Kempe probeerde
aan te tonen dat deze vijf vormen allemaal te verkleinen zijn.
Als dat hem lukte had hij immers bewezen dat er geen
"Kleinste Tegenvoorbeeld"' bestaat, dus dat elke kaart
met 4 kleuren te kleuren is. Helaas faalden zijn pogingen bij de
vijfhoek.
De conclusie voorlopig was dat elk kleinste tegenvoorbeeld
minstens één vijfhoek bevat. Maar bij de telstelling
concludeerden we al dat de kaart dan minstens 12 vijfhoeken
bevat. Dus een kaart met exact 12 landen moet uit 12
vijfhoeken bestaan. Dat is het twaalfvlak, maar we zagen ook al
dat die wél te kleuren is. Conclusie: een kleinste
tegenvoorbeeld bevat minstens 13 landen.
Omdat de vijfhoek vastliep ging men proberen de vijfhoek
te vervangen door een een andere vorm. Zo ontdekte men
bijvoorbeeld dat ook de volgende verzameling een
onvermijdelijke verzameling is: |
|
|
 |
|
|
De vijfhoek is te vervangen door
twee nieuwe figuren; twee vijfhoeken naast elkaar en een
vijfhoek naast een zeshoek. Misschien valt van deze twee nieuwe
figuren wél te bewijzen dat ze te verkleinen zijn.....
En als dat niet lukt gaan we de verzameling nog verder
uitbreiden, misschien dat het dán wel lukt...
Hoe produceer je zulke onvermijdelijke verzamelingen?
Dat kan met de methode van ONTLADING.
We zullen het met de verzameling hierboven demonstreren.
Stel dat er een kaart bestaat die geen van de vijf basisvormen
hierboven bevat.
Dan kan een vijfhoek van de kaart dus niet grenzen aan een
tweehoek, driehoek of vierhoek (want die zijn er niet) maar ook
niet aan een andere vijfhoek of aan een zeshoek (vanwege de
laatste twee figuren). Dus elke vijfhoek grenst alleen maar aan
landen met minstens 7 grenzen.
Geef nu elk land een elektrische lading.
Een vijfhoek krijgt lading +1, een zeshoek lading 0, een
zevenhoek lading -1, een achthoek lading -2 enz.
Als de kaart L5 vijfhoeken en L6 zeshoeken
en L7 zevenhoeken... heeft, dan geldt voor de totale
lading T van de kaart:
|
| T = 1 • L5 + 0 • L6
- 1 • L7 - 2 • L8 -
... = L5 - L7
- 2L8 - 3L9 - ..... |
|
|
De telstelling zegt: 2L2 + 3L3
+ 2L4 + L5 - L7 - 2L8
- 3L9 - ... = 12 en omdat L2 = L3
= L4 = 0 geeft dat L5 - L7
- 2L8 - ... = 12
Als we dat vergelijken met de formule hierboven concluderen we
dat de totale lading van de kaart 12 is.
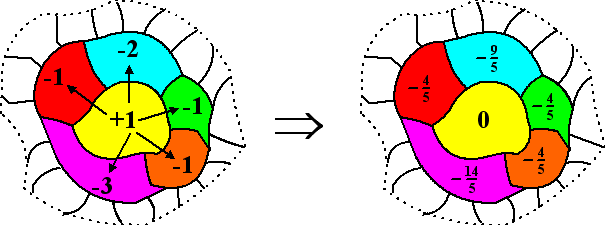
We gaan nu de lading herverdelen over de kaart. Als we alle
lading in de vijfhoeken herverdelen over zijn buren dan krijgt
elke buur er 1/5
bij. Dat zou er zó uit kunnen zien: |
|
|
Elke vijfhoek heeft na dit
ontladen dus lading nul. Verder heeft elke zeshoek óók lading
nul (immers die grensde niet aan een vijfhoek)
Hoe is het met de zevenhoeken? Die had lading -1 en moet dus, om
lading positief te krijgen van minstens 6 omringende vijfhoeken
lading ontvangen. Maar dat kan niet, want dan zouden minstens 2
van die 6 vijfhoeken aan elkaar grenzen, en dat mocht niet! De
conclusie is dat elke zevenhoek na afloop negatieve lading
heeft. |
 |
| Een achthoek zou zelfs van 11 aangrenzende
vijfhoeken lading moeten krijgen! |
|
| Dat kan duidelijk niet. En op
dezelfde manier zie je dat negenhoeken en hoger ook nooit
positieve lading kunnen krijgen. De conclusie is dat na ontladen
elk land lading nul of minder heeft. Maar toch moet de totale
lading 12 zijn gebleven! Dat is onmogelijk, dus de
oorspronkelijke aanname (dat een vijfhoek niet aan een zeshoek
of andere vijfhoek kan grenzen) niet juist. |
|
|
| Men ging dus op jacht naar
onvermijdelijke verzamelingen. Die werden groter en groter. In
1920 was men bij de volgende verzameling: |
|
|
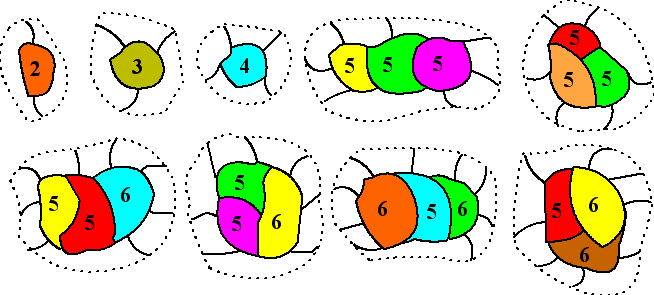 |
|
|
| In de loop van de twintigste eeuw
werden onvermijdelijke verzamelingen van duizenden figuren
gemaakt. Het werd steeds meer werk om te onderzoeken of ze
allemaal wel of niet te verkleinen waren, vooral ook omdat
verschillende vormen vaak verschillende manieren van ontladen
vereisten. |
|
|
| 2. Verkleinbare
Kaart |
|
|
Zoals we al eerder zagen
is een Verkleinbare Kaart een kaart die je niet kunt
kleuren met 4 kleuren, maar waarvoor je kunt aantonen
dat je een kleiner deel van die kaart dan óók niet met
4 kleuren kunt kleuren. De aanpak was eigenlijk zoals
Kempe het al deed.
Maar in 1913 kwam daar verandering in door een
publicatie van George David Birkhoff.
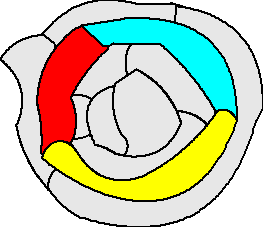
Birkhoff keek niet naar aparte landen, maar beschouwde
een RING van landen in een kaart.
Hiernaast staat zo'n ring van drie landen.
Als deze kaart een Kleinste Tegenvoorbeeld is, dan is
het gebied van ring + binnenste dus te kleuren.
Hetzelfde geldt voor het gebied van ring + buitenste.
Maar dan kunnen we die beide kleuringen gewoon
samenvoegen (eventueel door sommige kleuren een andere
naam te geven) om de hele kaart te kleuren.
Conclusie: een kaart met een ring van drie landen
is verkleinbaar, dus in een Kleinste Tegenvoorbeeld kan
niet zo'n ring van 3 landen voorkomen. |
|
|
| Wat Kempe land voor land deed
gebeurt nu eigenlijk met groepen van landen tegelijk.
Voor een ring van 4 landen is het al wat moeilijker want
die kan gekleurd zijn met 2, 3 of 4 kleuren en het is niet
duidelijk of de kleuringen van binnen- en buitengebied kloppend
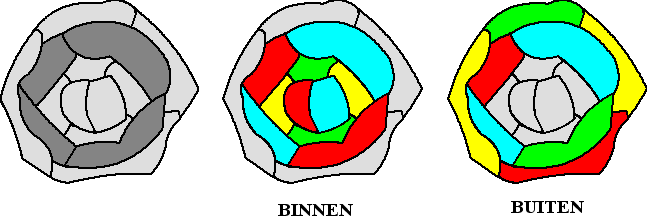
gemaakt kunnen worden op de ring. Het volgende geval is
bijvoorbeeld niet kloppend te krijgen: |
|
|
 |
|
|
Maar Birkhoff slaagde erin kleuren
te wisselen (jawel via Kempe Ketens!) zodat de kleuringen toch
dekkend te krijgen waren. Ook de ring van 5 wist hij in bijna
alle gevallen kloppend te krijgen. Bijna? Ja, de enkele vijfhoek
omringd door een ring van vijf landen lukte niet. Hetzelfde
geval waarop Kempe was vastgelopen!
Het geval van een ring van zes was nog lastiger... Dat werd pas
30 jaar later opgelost!
Ook een moeilijk geval bleek "The Birkhoff
Diamond". Een analyse daarvan is kenmerkend voor de
methodes die nodig waren en de hoeveelheid
mogelijkheden die onderzocht moesten worden. Het staat HIER. |
|
|
En zo ging het de twintigste eeuw
door. Men werkte van twee kanten aan het probleem. Van de ene
kant vond men meer en meer (en steeds grotere) onvermijdelijke
verzameling. Van de andere kant slaagde men er langzaam in van
steeds meer figuren te bewijzen dat ze te verkleinen waren.
De
jacht was geopend!
De jacht die beide kanten van het onderzoek
zou doen samenkomen.
De jacht naar:
|
|
Een onvermijdelijke
verzameling
van alleen maar verkleinbare figuren
|
|
|
Immers als die bestaat dan bestaat er kennelijk géén
Kleinste Tegenvoorbeeld, dus is elke kaart met 4 kleuren te
kleuren.
|
|
|
|