Vreemd genoeg gaat dit
symmetriebewijs over een volledig asymmetrische figuur:
|
Neem een convexe n-hoek die geen
evenwijdige zijden heeft.
Kies een punt O binnen deze figuur.
Dan zijn er hoogstens n lijnen door O die de n-hoek
in twee stukken met gelijke oppervlakte verdelen.
Bewijs dat. |
|
|
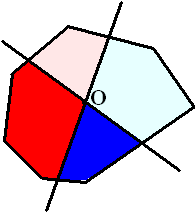
Hiernaast staat een voorbeeld van
zo'n n-hoek (in dit geval 7-hoek).
Er staan twee lijnen getekend die de 7-hoek in stukken met
gelijke oppervlakte verdelen.
Rood is dus even groot als blauw, maar ook licht even
groot als donker.
Maar omdat {donkerrood + donkerblauw = 1/2}
en {donkerrood + lichtrood = 1/2}
moet wel gelden dat {donkerblauw = lichtrood}. Op dezelfde
manier doorredenerend kunnen we concluderen dat alle vier de
delen een gelijke oppervlakte hebben.
Er lijkt geen symmetrie te bekennen, maar die voeren we zelf in
door de hele figuur te spiegelen in O.
dat is in de onderste figuur gebeurd. |
 |
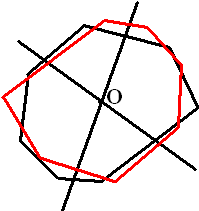
De twee getekende lijnen verdelen de figuur in 4 kwadranten.
Binnen elk van deze kwadranten moeten de zevenhoek en zijn
spiegelbeeld elkaar snijden. Immers de oppervlakte van de vier
delen was gelijk. Als er geen snijpunt is, dan ligt het ene deel
helemaal buiten het andere en heeft dus een grotere oppervlakte.
(de lijnstukken kunnen niet gedeeltelijk samenvallen omdat van
de oorspronkelijke zevenhoek geen twee zijden evenwijdig waren)
Door twee lijnen te tekenen krijgen we dus 4 kwadranten en
noodzakelijkerwijs ook 4 snijpunten van zevenhoek met
spiegelbeeld. |
 |
|
|
Als we nu k zulke lijnen in
de veelhoek tekenen krijgen we 2k hoeken in het midden en
dus ook 2k sectoren. Dus zouden er ook minstens 2k
snijpunten tussen oorspronkelijke figuur en spiegelbeeld moeten
zijn.
Omdat elke willekeurige rechte lijn de zijden van een (convexe!)
veelhoek hoogstens twee keer kan snijden kunnen n rechte
lijnstukken hoogstens 2n snijpunten met een veelhoek
hebben.
De enige mogelijke conclusie is daarom dat 2k
≤ 2n ofwel k
≤ n |