|
De
Ketens van Kempe |
|
|
We zagen dat we
vastliepen bij de vierhoek en de vijfhoek om te bewijzen dat KT
niet bestaat.
In 1880 publiceerde Alfred Bray Kempe een artikel waarin hij die
twee problemen oploste!
Daarmee was het vierkleurenprobleem opgelost!!!
Tenminste.....
Dat dacht de hele wiskundewereld 9 jaar lang.
Hier volgt een beschrijving van het bewijs van Kempe; het meest
beruchte foute wiskundebewijs uit de geschiedenis. |
|
|
| 1. De Vierhoek
opgelost. |
|
|
We zagen dat we
vastliepen als we een vierhoek uit de KT weglaten, de rest
kleuren en dan de vierhoek weer willen invoegen. Het zou dan
namelijk kunnen dat alle vier de buren van de vierhoek een
verschillende kleur hebben zodat er geen kleur meer over is voor
de vierhoek zelf.
Stel dat de situatie rond de vierhoek op het moment van invoegen
is als hiernaast.
Dan is de vierhoek (en dus de kaart) niet te kleuren.
Kempe vond een oplossing: |
 |
| Hij koos twee kleuren
rond de vierhoek die niet aangrenzend zijn. Bijvoorbeeld in de
figuur hierboven geel en groen. Met deze twee landen maakte hij
vervolgens een keten van alleen maar groene en gele landen die
aan elkaar grenzen. Dat gaf een figuur als rechts hiernaast.
Alle niet-gekleurde landen zijn blauw/rood, of toch geel/groen
maar dan zijn ze niet via de groen-gele ketens te bereiken.
Nu zijn er twee mogelijkheden:
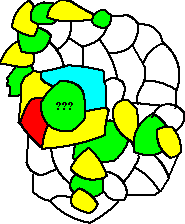 |
A. |
De twee gekleurde groen-gele ketens
ontmoeten elkaar niet.
Dat is het simpelste geval. We kiezen in dat geval
gewoon één van beide takken, en wisselen van die tak
ALLE landen van kleur (groen wordt geel en geel wordt
groen). Dat kan omdat de tak nergens aan een ander groen
of geel land grenst, en ook bij de begin-vierhoek waren
groen en geel niet-aanliggend.
Dat heeft als gevolg dat nu de probleemvierhoek nog maar
door drie kleuren is omringd, dus is hij te kleuren met
de vierde kleur.
Links hiernaast is dat voor de bovenste tak
gebeurd. |
|
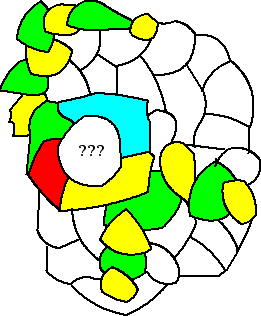 |
|
|
| B. De groen-gele
ketens komen wél bij elkaar. |
|
|
|
Dan werkt dat wisselen
niet, want dan wisselen beide landen die aan de probleemvierhoek
grenzen van kleur en zijn er weer 4 kleuren.
Kempe's oplossing was eenvoudig: in dat geval schakelen we over
naar de blauw-rode ketens!
Die kunnen niet óók bij elkaar komen omdat óf het blauwe óf
het rode land geheel ingesloten is door de geel-groene keten.
Dus voor de rood-blauwe ketens geldt in ieder geval situatie A,
en door één van beiden te wisselen van kleuren is de vierhoek
weer in te passen. KLAAR! |
|
|
| 2. De
Vijfhoek opgelost |
|
|
|
We hebben het dan over
de probleemsituatie als hiernaast.
Kies weer twee verschillende kleuren die niet aangrenzend zijn.
Ga weer ketens maken. Als die ketens elkaar niet ontmoeten
(geval A) zijn we weer klaar: we wisselen de keten die begint
bij de kleur waarvan er maar één aan de vijfhoek grenst.
We gaan meteen naar geval B: stel dat deze ketens elkaar wél
ontmoeten. Stel bijvoorbeeld dat in de figuur hiernaast
geel-blauw elkaar ontmoeten.
dan schakelen we over op geel rood.
We nemen maar meteen aan dat ook die elkaar ontmoeten want
anders hebben we weer geval A en zijn we klaar. De situatie
waarmee we te maken hebben is dus dat zowel geel-blauw als
geel-rood elkaar ontmoeten:
|
 |
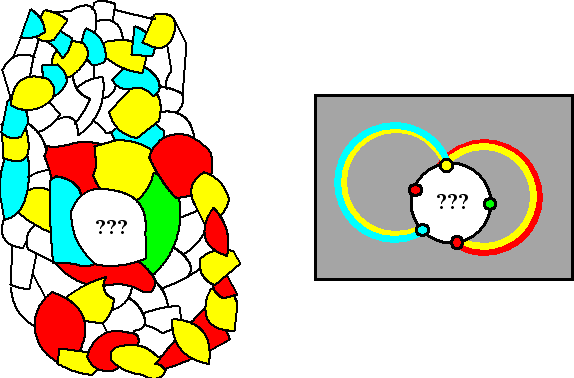 |
|
|
| De situatie is rechts
schematisch weergegeven. De groen-blauwe takken zijn nu nooit
met elkaar verbonden omdat de rood-gele lijn die verbinding
blokkeert. Dus kunnen we die tak wisselen zodat het groene land
ook blauw wordt. |
"Ho
wacht even: nou heb ik je", hoor ik je al
denken, met in je achterhoofd het idee dat jij slimmer bent dan
de hele wiskundewereld 9 jaar lang. Als we in plaats van
groen-blauw nu groen-rood hadden gekozen dan gaf dat geen
oplossing omdat dan bij wisselen het rode punt groen zou
worden, en daar schieten we niets mee op. En het groene
rood laten worden mág niet eens want het groene land grenst aan
rood... Klopt dit wel? Is dit geen gezocht voorbeeld.
Nee, dit is niet de fout. Dat kiezen kan altijd. Dat kun je als
volgt zien.
Laten we de kleuren 1,2,3,4,4 noemen (er is altijd één dubbele
en die noemen we 4.
Laat de volgorde rond de cirkel 1,2,4,3,4 zijn. Dat is nog
steeds het algemene geval, immers 1,2,3 kunnen we onderling
hernummeren, en als de volgorde 1,4,2,3,4 is dan spiegelen we de
figuur gewoon. Maak ketens van 1 naar 4 en van 1 naar 3 als
hiernaast.
Dan is de keten van 2 naar 3 niet verbonden dus kunnen we
bijvoorbeeld 2 wisselen naar 3.
WATERDICHT! |
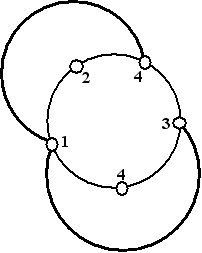 |
|
|
Kortom: een KT
heeft geen 2- 3- 4- en 5-hoek want dan is er een kleinere kaart
niet te kleuren.
Maar elke kaart heeft een 2- 3- 4- of 5-hoek.
Dus KT bestaat niet.
Het 4-kleurenprobleem is OPGELOST!
tja.................................... |
|
|