Nieuwe pagina 1

Het Isoperimetrisch probleem

.....want zo staat dit beroemde probleem ook wel bekend.

Dit probleem komt zelfs voor in de klassieke geschiedenis. Vergilius beschrijft de avonturen van koningin Dido. Deze koningin bleek zowaar een goede wiskundige te zijn! Haar vader werd door haar broer vermoord, en die broer richtte vervolgens zijn "aandacht" op Dido. Zij was gedwongen haar geboorteplaats Tyria in Phenicië te ontvluchten.
Uiteindelijk landde haar schip in Afrika. Daar bood zij het plaatselijke opperhoofd al haar waardevolle spullen aan in ruil voor zoveel land als zij met de huid van een os zou kunnen omgrenzen. Men ging akkoord en een grote os werd geofferd. Dido sneed de huid in extreem dunne repen en omgrensde langs de kust een enorm gebied in de vorm van een halve cirkel.
Op dit stuk land ontstond de stad Carthago.....

Maar terug naar het bewijs. Dat gaat in vier stappen.

STAP 1

"De figuur met de grootste oppervlakte moet convex zijn."

In normaal Nederlands betekent dat dat er "geen deuken en gaten in mogen zitten"
Wiskundig geformuleerd betekent het dat voor elke twee willekeurige punt A en B van de figuur het lijnstuk AB zich geheel binnen de figuur bevindt.

Het bewijs is erg eenvoudig. Kan zelfs op twee manieren.

1^e manier:
Stel dat een lijnstuk AB deels buiten de figuur ligt. Dan kun je de twee snijpunten die AB met de omtrek van de figuur heeft door een rechte lijn met elkaar verbinden. En een rechte is de kortste verbinding tussen twee punten, dus is de omtrek minder geworden. De twee niet-convexe figuren hierboven hebben hiernaast een kleinere omtrek en een grotere oppervlakte gekregen.

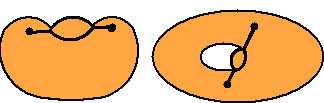
2e manier:
Spiegel het deel van de omtrek dat aan de "verkeerde" kant van AB ligt in AB. Dat geeft een nieuwe figuur met even grote omtrek en grotere oppervlakte.
Kijk maar naar de figuren hieronder.

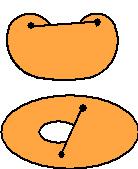STAP 2

De figuur met de grootste oppervlakte moet symmetrisch in elke diagonaal zijn

Een diagonaal noemen we een rechte lijn die de omtrek van de figuur in twee gelijke delen verdeelt.
Stel dat we de figuur met de grootste oppervlakte hebben gevonden, en dat er een diagonaal is waarin hij niet symmetrisch is.
Dan kunnen we de grootste helft (qua oppervlakte; als de helften even groot zijn kies er dan zomaar eentje) van de figuur spiegelen in die diagonaal. Dat geeft een nieuwe figuur die wél symmetrisch is met een even grote omtrek en een minstens even grote oppervlakte.
Maar dat is in strijd met het gegeven dat onze oorspronkelijke figuur de optimale was!

Omdat de figuur die we zoeken dus symmetrisch in elke diagonaal is, kunnen we ons vanaf nu beperken tot de helft van zo'n figuur. We bekijken daarom vanaf nu alleen vormen die boven een rechte lijn AB (een diagonaal) liggen.

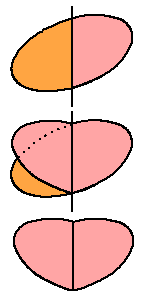STAP 3

Een willekeurig punt C op de figuur maakt een rechte hoek op AB

Kies een willekeurig punt C op de rand van de figuur en trek de lijnen CA en CB. Dat verdeelt de (halve) figuur in drie delen; één driehoek ABC en twee andere delen. Stel je nu voor dat beide andere delen van solide materiaal zijn gemaakt, en in C scharnierend aan elkaar vast zitten. Door ze te draaien verandert de oppervlakte van de beide solide delen niet, maar alleen de oppervlakte van de driehoek:

Dus hoeven we alleen nog maar te zoeken naar de grootste gele driehoek. Ofwel: welke driehoek, waarvan twee zijden bekend zijn heeft de grootste oppervlakte?

Dat blijkt degene te zijn met een rechte hoek C!

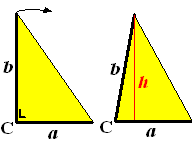
Dat kun je hiernaast zien. Neem een rechthoekige driehoek met vaste zijden a en b.
De oppervlakte is dan gelijk aan ¹/₂ • a • b

Maak de hoek bij C nu ongelijk aan 90º (in de tekening kleiner, maar bij groter is het verhaal hetzelfde). Dan is de oppervlakte van de nieuwe driehoek ¹/₂ • a • h.
Maar h is kleiner dan b (h is een rechthoekszijde in een driehoek waarin b de schuine zijde is)

Dus is de oppervlakte kleiner geworden. Dus heeft de driehoek met een hoek van 90º de grootste oppervlakte.

STAP 4

De figuur met bij elke C een rechte hoek op AB is een cirkel.

Dat is heel simpel hiernaast in te zien.
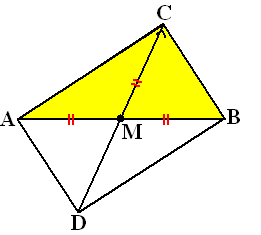
Neem een driehoek ABC met een rechte hoek C. Noem M het midden van AB.
Maak van de driehoek een rechthoek.
De diagonalen van een rechthoek zijn even lang en snijden elkaar doormidden.
De ene diagonaal is AB, en de andere diagonaal is CD.
Dus CM = AM = MB. Dus punt C ligt even ver van M af als A en B.
Dus ligt C op een cirkel met middelpunt M en straal MA.

Kortom: 't is een cirkel!

En toch klopt dit bewijs niet!
We hebben een wiskundige blunder gemaakt!!

Dat zit hem in het volgende.
Ons "bewijs" kwam eigenlijk in grote lijnen op het volgende neer:

1. Stel dat een figuur die geen cirkel is toch de grootste oppervlakte heeft
2. Dan kunnen we die figuur veranderen in een nieuwe figuur die een grotere oppervlakte heeft.
3. Dus had onze figuur niet de grootste oppervlakte.
4. Dus heeft een cirkel de grootste oppervlakte

En toch is dit een foute redenering.
Kijk: het volgende "bewijs" gaat precies hetzelfde; en ziet er zó uit:

Gegeven een lijnstuk, AB en een lijn l die evenwijdig is.
Welk punt D op l heeft de kleinste hoek ADB?
We gaan de grote lijnen van hierboven volgen:


1.	Stel dat we een punt D₁ hebben gevonden dat niet hetzelfde is als C, en dat de kleinste hoek AD₁B geeft.
2.	Dan kunnen we dat punt D₁ veranderen in een punt D₂ verder van C af dat een kleinere hoek AD₂B heeft.
3.	Dus had D₁ niet de kleinste hoek
4.	Dus heeft punt C de kleinste hoek ACB

Waar is het bewijs fout gegaan?
Het ging er vanuit dát er een figuur is die maximale oppervlakte heeft.
Vooral bij stap 2 is dat meerdere malen gebruikt.

Nou is er natuurlijk wél een verschil: onze cirkel-oppervlakten gingen steeds dichter naar een cirkel toe, en de rare hoeken van hierboven gaan steeds verder van het optimum áf. Maar het gaat om het idee. Logisch gezien klopt het bewijs niet.

Dit manco blijkt nogal moeilijk op te lossen. Je hebt er het begrip "compactheid" voor nodig. Dat geeft aan wanneer er limiet-oplossingen bestaan en wanneer niet. Maar 't is allemaal geen makkelijke wiskunde!