Stel dat de stelling voor n klopt. Voeg dan  ¹/_{(n + 1)²} toe. Dat geeft:

Voor het eerste ongelijkteken is de inductieaanname gebruikt.
Het laatste ongelijkteken moet nog bewezen worden, maar dat kan natuurlijk nooit! Je kunt immers  nooit bewijzen dat ³/₄ plus iets kleiner of gelijk is aan ³/₄. ONZIN!

De tweede stelling.

Op dezelfde manier vinden we nu:

Weer moet het laatste ongelijkheidsteken nog bewezen worden.
Maar nu kan het ineens wél, namelijk als we het volgende kunnen bewijzen:

En dat is een makkie: vermenigvuldig alles met n • (n + 1)², dat geeft:  -(n + 1)² + n + n • (n + 1) ≤ 0
ofwel   -n² - 2n - 1 + n + n² + n ≤ 0  ⇒  -1 ≤ 0  en dat is overduidelijk waar!

Een verwant probleem met dezelfde rare eigenschap


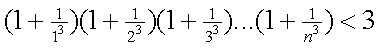
Deze is niet eenvoudig te bewijzen. Echter de volgende strengere eigenschap wel:


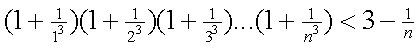
Noem de linkerkant A_n.

STAP 1
Voor n = 1 staat er  2 < 2¹/₂ en dat is duidelijk waar

STAP 2
Stel dat de eigenschap geldt voor An
Dan geldt:


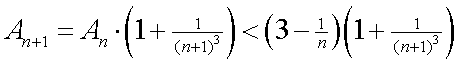
Voor het < teken is de inductie-aanname gebruikt.
Haakjes wegwerken, en breuken samennemen:


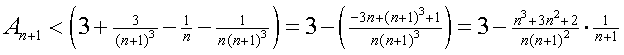
Als we nu kunnen bewijzen dat:

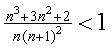
Dan staat er de eigenschap voor A_{n + 1}
Dus is de vraag  n³ + 3n² + 2 < 1 • n(n + 1)²
Dat reduceert tot  n² - n + 2 < 0
De discriminant is (-1)² - 4 • 1 • 2 = -7  en als je zomaar een n invult is te zien dat inderdaad altijd geldt dat de linkerkant kleiner is dan nul.

Daarmee is het inductiebewijs af.