| De Kaart van
Haewood |
|
In 1889 kwam helaas Haewood met
een voorbeeld waaruit bleek dat het "bewijs"van Kempe
niet klopte. Het zat hem in de redenering rondom de vijfhoek.
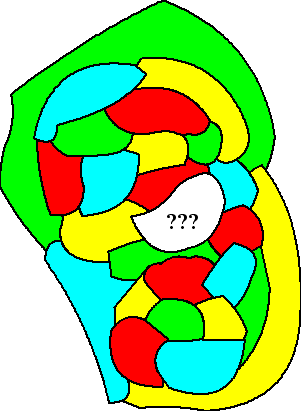
De kaart die Haewood gebruikte lijkt ongeveer op die hiernaast.
Laten we de methode van de ketens van Kempe maar gewoon gaan
toepassen, dan zien we vanzelf waar de boel vastloopt.
We zien bijvoorbeeld dat blauw-geel langs de
onderklant met elkaar verbonden is. En ook blauw-groen langs de
bovenkant. Rood is nergens mee verbonden. De situatie is als
volgt:
|
 |
Maar verhip! Wat krijgen we nou?
De banen blauw-geel en blauw-groen kunnen elkaar natuurlijk wél
doorkruisen, in een BLAUW land!
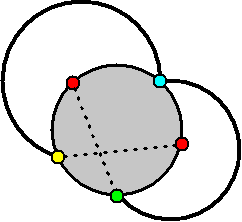
We kunnen rood-geel onderlangs wisselen (gescheiden door
de blauw-groene boog) en we kunnen ook rood-groen
wisselen(gescheiden door de blauw-gele boog). De stippellijnen
geven de mogelijke wisselingen aan.
Maar we kunnen niet BEIDEN wisselen! Dan komen er twee rode
landen naast elkaar te liggen! Dat had Kempe niet gezien!
Ook in de figuur hiernaast kan dat niet.
Helaas... Het bewijs van Kempe was fout!
En de fout was ook niet zomaar te repareren. |
 |
|
|
Maar laten we het positieve van
het werk van Kempe nemen: het
bewijs met de vierhoek van Kempe klopt wél, en zijn methode van
de ketens kan gebruikt worden om de vijfhoek te bekijken. Stel
dat we een kaart met VIJF kleuren willen kleuren.
We kunnen dan bij de vijfhoek wel twee niet-aanliggende
verschillende kleuren nemen, ketens maken en kijken of die
elkaar ontmoeten. Als dat niet zo is wisselen we, als het wél
zo is zijn er in ieder geval twee andere kleuren waarvan de
ketens elkaar niet ontmoeten. Die kunnen we dan wisselen, zodat
er rond de vijfhoek nog maar vier kleuren aanwezig zijn, en de
vijfde kleur voor de vijfhoek zélf beschikbaar is.
Conclusie:
|
| Elke kaart is met 5 kleuren
in te kleuren. |
|
|
|
| Nog maar één kleurtje weg te werken.... |
|