De e-pagina

© h.hofstede (h.hofstede@hogeland.nl)

 
We bekijken de afgeleide functie van een machtsfunctie  f(x) = gx. 
Daarvoor geldt (met dx zo klein mogelijk):
 
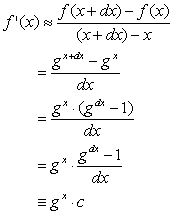Daarna rijst bij iedereen die een beetje gevoel voor wiskunde heeft onmiddellijk de vraag: is er ook een g waarvoor de constante gelijk is aan 1? Ofwel: welke functie gx is gelijk aan zijn eigen afgeleide?
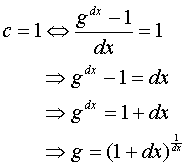Nog steeds in ons achterhoofd dat dx zo klein mogelijk moet zijn . Hoe kleiner, des te beter.
Dat geeft de volgende tabel:
dx g
0,1 2,59374246....
0,01 2,704813829...
0,001 2,716923932...
0,0001 2,718145927...
En zo zien we langzaam maar zeker ons getal e ontstaan.
In ieder geval weten we dus:        f(x) = ex  ⇒  f '(x) = ex
De Taylor-reeks.
Stel dat we een functie f(x) kunnen benaderen door een polynoom.
Dus dat zou gelden:  f(x) = c0 + c1x + c2x2 + c3x3 + ...
De formule moet dan ook gelden voor x = 0.
Dat geeft  f(0) = c0
Vervolgens bekijken we de afgeleide:
f '(x) = c1 + 2c2x + 3c3x2 + 4c4x3 + ....
Maar voor x = 0 geeft dat  f '(0) = c1
De volgende afgeleide levert zo  f ''(0) = 2c2 + 2 • 3 • c3x + ...    ofwel  c2 = f ''(0)/2
De volgende geeft  f '''(0) = 2 • 3 • c3 + 3 • 4 • c4 • x + ....   ofwel  c3 = f '''(0)/(2 • 3)

Zo doorgaand vinden we achter elkaar alle c-waarden
Dat levert de formule van Taylor:
Laten we hem meteen maar toepassen op  f(x) = ex. Dan zijn alle afgeleiden  f n(0) gelijk aan 1.
Dat geeft:
Het bewijs dat e geen breuk is.
Stel dat e te schrijven is als  p/q met p en q positieve gehele getallen.
Vermenigvuldig de reeksontwikkeling voor e aan beide kanten met q! Dat geeft:
Omdat de linkerkant een geheel getal is (e is immers p/q) moet de rechterkant ook een geheel getal zijn.
Het eerste deel rechts bestaat uit allemaal gehele getallen en is dus geheel.
Dus moet het tweede deel ook een geheel getal zijn. Noem dat deel R
Dan geldt:
In de derde stap hebben we de noemers kleiner gemaakt, dus is de som van de breuken groter geworden, dus groter dan R. Het deel op de laatste regel tussen haakjes is precies een meetkundige rij met reden 1/(q+1). Daarvan is de som bekend. Substitueren levert:
Omdat R en q beiden positief zijn hebben we nu een positief getal R gevonden waarvoor geldt  0 < R < 1/q
Dat kan niet, dus is de oorspronkelijke aanname dat e geschreven kan worden als p/q onjuist. Conclusie:
e is geen breuk!
 
© h.hofstede (h.hofstede@hogeland.nl)