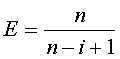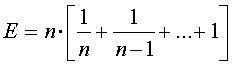|
Wat gaat mijn verzameling kosten?
Om een nieuwe soort chips te introduceren is de fabrikant een reclameactie
begonnen waarbij in elke zak een FLIPPO wordt gestopt. Er zijn 10 verschillende
FLIPPO's die in gelijke aantallen over alle chipszakken zijn verdeeld.
Mijn zoontje is een verwoed verzamelaar en zal net zolang blijven zeuren tot
hij ze allemaal heeft.
Hoeveel gaat deze onzin mij kosten?
Hoeveel zakken zal ik gemiddeld moeten kopen om alle 10 de verschillende
FLIPPO's te hebben?
Definieer daarvoor eerst Ai = aantal zakken dat nodig is om de ide
flippo te krijgen (dus als ik er al i-1 heb)
Ik geef eerst een rekenvoorbeeld voor A7:
Als ik al 6 flippo's heb zijn er nog 4 flippo's niet in mijn bezit,
dus is de kans dat ik de 7de in een nieuwe zak vind gelijk
aan 0,4
Voor het aantal zakken dat daarvoor nodig is geldt de volgende
kansverdeling:
| aantal |
kans |
1
2
3
4
...
n |
0,4
0,6 • 0,4
0,62 • 0,4
0,63 • 0,4
....
0,6n - 1 • 0,4 |
de verwachtingswaarde daarvan is :
E =
0,6•E =
0,4•E =
0,6•0,4•E =
0,4•E - 0,24•E = |
1 • 0,4 +
1 • 0,4 +
1 • 0,4
|
2 • 0,6 • 0,4 + 3 • 0,62 • 0,4
+ ...
1 • 0,6 • 0,4 + 2 • 0,62 • 0,4 + 3 • 0,63
• 0,4 + ...
1 • 0,6 • 0,4 + 1• 0,62 • 0,4 + 1 • 0,63
• 0,4 + ...
1 • 0,6 • 0,4 + 1 • 0,62 • 0,4 + 1 • 0,63
• 0,4 + 1 • 0,64 • 0,4 + ... |
E • (0,4 - 0,6 • 0,4) = 0,4 dus E • (1 - 0,6) =
1 dus E = 1 / 0,4 = 2,5
conclusie: E = 2,5
|
Deze berekening kunnen we uiteraard precies zo herhalen met 10 = n
en 7 = i
Dan is 0,4 = (n - i + 1)/n en 0,6 = (i
- 1)/n
Dat geeft als verwachtingswaarde:
Voor het totaal aantal benodigde zakken moeten we dit nog sommeren van i
= 1 tot i = n:
Voor de flippoverzameling geldt bijvoorbeeld dat E »
29,3 ofwel ik zal gemiddeld ongeveer 29 zakken chips moeten kopen voordat mijn
zoontje ophoudt te zeuren.
Een tabel en een grafiek:
| n |
E(n) |
1
2
3
4
5
6
7
8
9
10 |
1
3
5,5
8,3
11,4
14,7
18,2
21,7
25,5
29,3 |
|
| n |
E(n) |
11
12
13
14
15
16
17
18
19
20 |
33,2
37,2
41,3
45,5
49,8
54,1
58,5
62,9
67,4
72,0 |
|
| n |
E(n) |
21
22
23
24
25
26
27
28
29
30 |
76,6
81,2
85,9
90,6
95,4
100,2
105,1
110,0
114,9
119,8 |
|
|
|
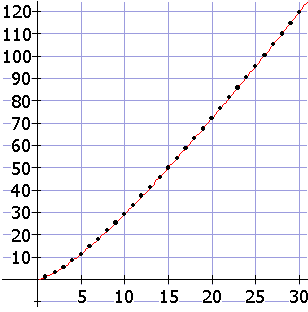 |
De doorgetrokken lijn in de grafiek is de volgende benadering:
1 + 1/2 + 1/3 + ...+ 1/n
= ln(n) + g + 1/(2n)
(met g = 0,57722... constante van Euler)
Dus E(n) » n• ln(n)
+ g • n + 1/2
en dat is de getekende grafiek. Je ziet dat het een prima
benadering is.
Aan deze gegevens kunnen we bijvoorbeeld ook zien dat:
• je gemiddeld 14,7 keer moet gooien voordat je met een dobbelsteen alle
getallen van 1 tm 6 hebt gegooid.
• in een klas van 24 leerlingen waar iedere les willekeurig iemand
overhoord wordt het gemiddeld 90,6 lessen duurt voordat iedereen aan de beurt is
geweest.
|