|
Wegneemspellen (1 stapel)
Dit gaat over spellen waarin twee spelers om de beurt, volgens bepaalde
regels, een aantal fiches weg mogen nemen van een stapel. Wie de laatste legale
zet doet heeft gewonnen.
Voor dit soort spellen definieren we het Grundy-getal g. (naar
Grundy (1939) die dit introduceerde). Een eindpositie, dat is een positie
waaruit geen zet meer mogelijk is, heeft g = 0. Voor elke andere
positie bepalen we het g-getal als volgt:
|
Bekijk de verzameling van alle
positie die uit de gegeven positie bereikt kunnen worden in één zet.
Schrijf
de verzameling G van alle g-getallen van die posities op.
Het nieuwe g-getal
is nu het kleinste niet negatieve getal dat niet in G zit.
|
- Het doel van het spel is nu om voor je tegenstander een positie met g-getal
0 neer te leggen.
- Hij moet dan voor jou altijd een positie met g > 0 wegleggen.
Hij kan niet wéér een g = 0 positie maken, want een positie die uit
een andere volgt heeft altijd een andere g.
- Van die nieuwe positie maak jij weer een g = 0 positie. Dat kan
gegarandeerd want g = 0 zit zeker in de opvolgposities want als dat
niet zo was, dan had deze postie zelf wel g = 0 gehad.
- En dat gaat zo alsmaar door totdat je een eindpositie voor hem
weglegt.
spel 1. Je mag per keer 1,2 of 3 fiches wegnemen
De eindpostie met 0 fiches heeft g0 = 0
Uit de positie met 1 fiche kan alleen 0 bereikt worden, G = {0}, dus positie 1
heeft g1 = 1
Uit de positie met 2 fiches kunnen 1 en 0 bereikt worden; G = {0,1}, dus
positie 2 heeft g2 = 2
Uit de positie met 3 fiches kunnen 2, 1 en 0 bereikt worden; G = {0,1,2}, dus
positie 3 heeft g3 = 3
Uit de positie met 4 fiches kunnen 3,2 en 1 bereikt worden; G = {1,2,3}, dus
positie 4 heeft g4 = 0
Uit de positie met 5 fiches kunnen 4,3 en 2 bereikt worden; G = {2,3,0}, dus
positie 5 heeft g5 = 1
enz....
Zo vinden we automatisch de winnende posities: die met 0, 4, 8,
12,.... fiches.
De winnende taktiek is dus: Ga zo snel mogelijk naar een 4-voud toe en blijf
viervouden maken. Dat kan gegarandeerd, want als je tegenstander 1,2 of 3 fiches
weghaalt, dan haal jij er 3,2,of 1 weg. Uiteindelijk zul je de laatste fiche
weghalen.
ALGEMENERE AANPAK
Laten we de verzameling die je weg mag halen S noemen.
In het net genoemde voorbeeldspel was dus S = {1,2,3}
spel 2. S = {1,3,4} (dus per keer mag je
1, 3 of 4 fiches weghalen)
De g-waarden worden nu als volgt:
| n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
... |
| gn |
0 |
1 |
0 |
1 |
2 |
3 |
2 |
0 |
1 |
0 |
1 |
2 |
3 |
... |
De g-waarden zijn periodiek met periode 7.
Onze taktiek wordt: bereken n (mod 7) en maak daar 2 of 0 van.
Als er bijvoorbeeld 39 fiches liggen, dan bereken je 39(mod 7) = 4 en om g
= 0 te bereiken moet je dus 4 of 2 fiches weghalen.
Is de g-rij altijd periodiek? Dat zou mooi zijn!
Jazeker, mits de verzameling S eindig is. Dus dan is er altijd een winnende
strategie te vinden.
Een paar speciale gevallen:
1. S = {1, p} heeft de g-serie:
Als p
oneven is: g(n) = 01010101.....
Als p
even is : g(n) = 010101...012 waarbij er 0,5p
paren 01 aan de 2 vooraf gaan.
2. S = {1,2,..., p} dan is g(n)
= 012...p dus de nieuwe taktiek wordt: kies als winnende positie
een veelvoud van p + 1
Varianten
Een paar varianten maken de winnende speelwijze minder makkelijk te vinden en
zijn dus eigenlijk veel interessanter:
variant 1. Neem S oneindig groot.
| vb1 |
S = {alle priemgetallen behalve 1 en 2}
geeft g(n) = 00011122230341430341... |
|
|
| vb2. |
S = {alle Fibonacci getallen}
geeft g(n) = 012301234501230123450.... |
variant 2. Maak S afhankelijk van n
| vb: |
Je mag alleen een aantal fiches weghalen dat een deler is
van het totale aantal in de stapel. |
|
g(n) = 0121312141213... |
variant 3. Maak S afhankelijk van het aantal dat de vorige
speler nam.
| vb1: |
Schuh's Game: |
|
S = {1,2,3,..., p}, maar twee opeenvolgende
weggenomen aantallen mogen niet samen p + 1 zijn. |
|
winnende strategie:
maak de stapel een veelvoud van p + 2.
dat kan altijd, behalve als je tegenstander 1 fiche wegnam. In dat geval
neem jij er ook 1 weg, zodat er n•(p + 2) - 2
overblijven. Die positie kan je tegenstander nooit winnend maken, want
daarvoor zou hij p fiches moeten weghalen, en dat mag niet want
jij nam er 1 weg. |
| vb2: |
Binary Nim |
|
alles mag, dus S = {1,2,...} maar de eerste speler mag
niet de hele stapel wegnemen, en verder mag iemand nooit meer wegnemen
dan zijn voorganger deed. |
|
winnende strategie:
schrijf het aantal in de stapel binair en haal de kleinste macht van
2 weg (dus de eerste 1 vanaf rechts).
vb: er liggen 56 fiches, en 56 = 111000
dus je haalt er 8 weg.
dat geeft 48 = 110000. Je tegenstander moet het aantal even houden
(zodra hij het oneven maakt haal jij 1 fiche weg, en moeten jullie vanaf
dan om en om 1 fiche weghalen tot jij wint). Maar hij mag er niet meer
dan 8 wegnemen. Zijn zet zal altijd een nieuwe 1 in het binaire getal
produceren. Neem aan dat hij er 6 wegneemt. Dat geeft 42 = 101010.
Jij haalt er 2 weg, en dat geeft 40 = 101000. Vanaf nu blijven jullie om
en om 2 weghalen. Dat geeft de serie:
101000 - 100110 - 100100 - 100010 - 100000 - 011110 - enz.
Jij bent de enige die steeds het aantal enen in de binaire notatie
verkleint. Je zult dus vanzelf het laatste fiche nemen. |
| vb3. |
Fibonacci Nim |
|
alles mag, dus S = {1,2,...} maar de eerste speler mag
niet de hele stapel wegnemen, en verder mag iemand nooit meer wegnemen
dan het dubbele van wat zijn voorganger wegnam. |
|
winnende strategie:
Als het kan, neem dan de hele stapel.
In de andere gevallen schrijf je de stapel als een som van
Fibonacci-getallen en je neemt het kleinste Fibonacci getal weg. |
|
|
Weer een andere variant....
Het is natuurlijk ook erg leuk om verschil in de fiches te maken!
Laten we ze bijvoorbeeld nummeren van 1 tot en met n.
Om het helemaal wiskundig te maken stellen we als regel, dat je één
nummer per keer moet kiezen om weg te nemen, maar dat dan automatisch
alle nummers die daar een deler van zijn óók verdwijnen!
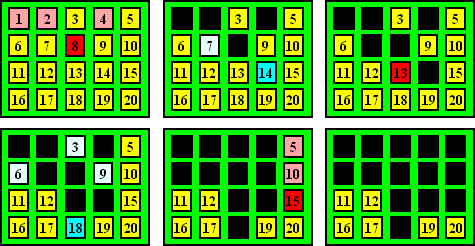
Een mogelijke variant met de nummers 1 tm 20 staat hieronder:
|
|
 |
|
|
Spelers rood en blauw wijzen om de beurt
een felgekleurd nummer aan, en ook alle lichtgekleurde delers daarvan
verdwijnen. De laatste zet van rood was duidelijk slim: er blijven nog 6
getallen over die geen delers onderling meer hebben. Dus zullen vanaf nu
rood en blauw om de beurt een nummer weghalen, dus rood het laatste
nummer!
De brandende vraag is natuurlijk: "Is er een
winnende strategie, en hoe hangt die van n af?"
Het is heel eenvoudig te bewijzen dat de eerste speler altijd kan
winnen, ongeacht van n.
Het bewijs daarvan gaat zó:
|
Stel dat we een tweede variant van het spel
spelen, met alle getallen tot en met n, maar zonder het
getal 1.
Als speler 1 deze tweede variant altijd zou kunnen winnen, dan
kan hij de eerste óók winnen door op dezelfde manier te
spelen, immers 1 verdwijnt altijd de eerste keer.
Als speler 2 deze tweede variant altijd zou kunnen winnen, dan
kan speler 1 de eerste variant winnen, namelijk door alleen het
getal 1 weg te halen. Dan gaan we immers daarna variant 2 spelen
met speler 2 aan de beurt! |
Mooi bewijsje hé?
We weten nu zeker dat er voor elke n een winnende variant voor
speler 1 is, maar zonder die variant te kennen!!!!
|
|
|
| EN NU OM GELD!!!!! |
|
|
Ik daag je uit het volgende eenvoudige wegneemspelletje met mij te spelen.
We leggen een groot aantal muntjes van 5, 2 en 1 eurocent in een lange
rij voor ons op tafel.
Om de beurt pakken wij een munt weg, maar het moet steeds één van de
buitenste twee zijn.
Bewijs dat bij een even aantal munten de eerste speler meestal het
meeste geld zal
winnen (in ieder geval NOOIT zal verliezen) en dat bij een oneven aantal
stenen de tweede speler meestal het meeste geld zal krijgen.
In bovenstaande rij (even aantal) kun je bijvoorbeeld altijd
winnen als je begint met de munt van twee eurocent rechts!
Hoe zit dat?
De oplossing is kinderlijk eenvoudig.
Laten we de munten om, en om groen en blauw kleuren:
De eerste speler kan er nu altijd voor kiezen om óf alle blauwe
munten te pakken, óf alle groene munten.
Als hij bijvoorbeeld alle groene munten wil, dan pakt hij de rechter
groene munt. Dat laat twee blauwe munten over voor de ander. Die moet
dus een blauwe pakken, en daardoor komt er weer een groene vrij. En dat
gaat zo alsmaar door.
De blauwe munten zijn samen 5 + 1 + 5 + 1 + 2 + 1 + 2 = 17
eurocent
De groenen zijn samen 2 + 1 + 2 + 5 + 2 + 5 + 2 = 19 eurocent.
Je kunt dus altijd winnen door de groenen te pakken: begin met de
munt van 2 eurocent!
Bij een oneven aantal kan speler 1 eerst een munt van de rand
wegnemen (de kleur daarvan ligt vast) en daarna kan speler 2 de taktiek
hierboven gebruiken. Speler 1 zal alleen winnen als de waarde van zijn
eerstgepakte munt meer is dan het verschil tussen de overblijvende
groene en blauwe rijen. Zelfs al heeft hij een munt méér!
|
|
|
|
|
|
|
|
|
|
|
|
|
|


