|
HEX
Op een bord als dit wordt het spel HEX gespeeld door de spelers ROOD en GEEL.
Om de beurt mogen beide spelers een zeshoek kleuren in hun eigen kleur. Wie als
eerste een doorlopende verbinding maakt tussen de buitengebieden van zijn eigen
kleur heeft gewonnen. Is er een winnende strategie te vinden, en zo ja, hoe
hangt die af van de grootte van het speelbord?
Eerst maar eens oefenen met het spel.
Waarschuwing: dit programma is ERG GOED; je wint niet zomaar!!!
|
|
SPEEL HEX
|
|
|
Op een 2x2 bord wint de eerste speler, dat is triviaal.
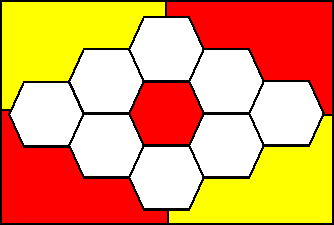
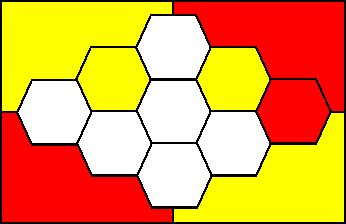
Op een 3x3 bord kan de eerste speler ook winnen door te beginnen de
centrale zeshoek te kleuren:
Rood wint in zijn derde zet. hij kan immers zowel naar rechtsboven als
naar linksonder op twee manieren zijn gebied bereiken, en geel kan slechts één
van deze twee manieren blokkeren.
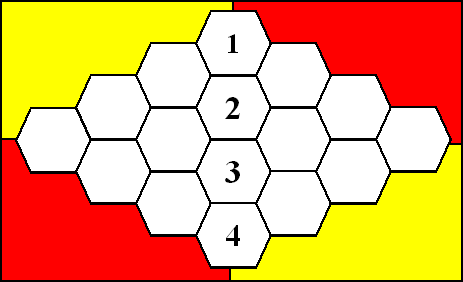
Op een 4x4 bord wordt het ingewikkelder. Het blijkt nu dat speler 1 kan winnen
door één van de vier genummerde velden als beginzet te kleuren.
Openen in veld 2 of 3 geeft winst met de vijfde zet. Openen met veld 1 of 4
geeft winst met de zesde zet.
Op een 5x5 bord kan nog bewezen worden dat de beginspeler kan winnen door
het centrale veld te kleuren, en dat hij op zijn zevende zet zal winnen.
Op grotere velden wordt de analyse enorm gecompliceerd. Een standaard
HEX-bord bestaat uit 11x11 velden!!!
Een volledige analyse op zo'n bord is onmogelijk. Er is geen winnende strategie
bekend, maar toch is te bewijzen dat speler 1 een winnende strategie moet
hebben! Dat bewijs gaat ongeveer als volgt:
| 1. |
Het spel kan geen gelijkspel worden, want
een speler kan de ander alleen blokkeren door zelf een doorlopende keten
te maken.
Er moet dus een winnende strategie voor óf de eerste óf de tweede
speler zijn. |
| 2. |
Neem aan dat de tweede speler een winnende
strategie heeft. |
| 3. |
Dan verdedigt speler 1 zich als volgt: Hij
doet eerst een willekeurige zet, en speelt daarna alsof hij speler 2 is.
Als hij volgens deze winnende strategie een zet moet doen op een veld
dat hij al gekleurd heeft, doet hij een willekeurige zet. Op deze manier
speelt hij dus de winnende strategie, alleen met één extra veld
gekleurd. |
| 4. |
Een extra gekleurd veld is nooit een
handicap om te winnen. Dus heeft speler 1 een winnende strategie. |
| 5. |
Er is dus geen winnende strategie voor speler 2. |
| 6. |
Dus er moet wel een winnende strategie voor speler 1
zijn. |
Tot slot zijn hier nog drie "Rood begint en wint" problemen:
PROBLEEM 1
PROBLEEM 2
PROBLEEM 3
|