| De
Driehoeksongelijkheid |
|
|
|
| De driehoeksongelijkheid zegt dat de twee
kortste zijden van een driehoek samen altijd langer zijn
dan de langste zijde. Voor een leek makkelijk in te zien;
kijk maar naar de driehoek hiernaast. Die ligt met de
langste zijde op de grond, en de andere twee zijn daaraan
scharnierend vastgemaakt. Je ziet meteen dat er alleen een
driehoek gemaakt kan worden als die twee elkaar ontmoeten,
en dat is zo als ze samen langer zijn dan de bodemzijde,
anders klapt de zaak in elkaar. |
|
Maar Euclides accepteerde
natuurlijk zo'n bewijs niet. Het moest netter, formeler en
preciezer.
Dat was niet iedereen met hem eens natuurlijk. Sommigen
dachten "wat een gekkigheid, waar is dat nou in
vredesnaam voor nodig?"
Commentator Proclus schreef:
De EpicuriŽrs maken dit
theorema belachelijk. Ze zeggen dat zelfs een ezel
dit kan inzien en dus is er geen bewijs voor
nodig. Het is het kenmerk van een domme man,
zeggen zij, om daar toch een bewijs voor te
vragen.
(...) Dat zelfs een ezel dit kan inzien is
duidelijk als je stro in het ene hoekpunt legt en
de ezel in het andere zet. Hij zal de weg langs de
ene zijde kiezen en niet langs beide anderen... |
Maar Euclides trok zich daar niets van aan
natuurlijk.
Hij bewees de driehoeksongelijkheid vanuit zijn axioma's:
Propositie
5 van de elementen bewijst dat de
basishoeken van een gelijkbenige driehoek gelijk zijn.
Daarvoor gebruikte hij een soort brugachtige figuur, en
deze propositie heet daarom ook de pons asinorum (brug
van de dommen; domme mensen zouden dit niet snappen en
deze "brug" niet over kunnen steken om het
beloofde land van de rest van de proposities binnen te
treden). |
|
|
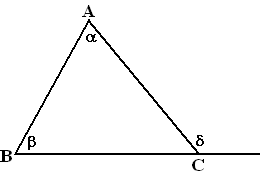
Propositie
16 laat zien dat de buitenhoek van een driehoek
groter is dan beide inwendige hoeken ertegen over.
In de figuur hiernaast betekent dat, dat d
groter is dan a en ook groter
dan b.
Dit was de eerste ongelijkheid die in de Elementen
voorkwam. |
 |
|
|
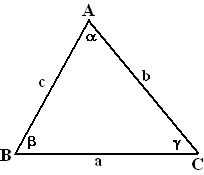
Propositie
19 zegt dat tegenover de grotere hoek
ook de grotere zijde ligt. In de figuur hiernaast betekent
dat, dat als b > a
dat dan ook AC > BC dus a > b
Ga uit van b > a.
Euclides beschouwde nu alle drie de mogelijkheden:
1. Stel b = a
Dan is de driehoek gelijkbenig, en propositie 16 zegt
dat de basishoeken gelijk zijn. Dat is in tegenspraak met b
> a dus kan niet
gelden b = a. |
 |
|
|
2. Stel dat b < a.
Als AC < BC dan kunnen we punt D op CB vinden zodat CD
= b
Dan geldt:
| b = |
binnenhoek van ABD |
| b<d |
buitenhoek van ABD: propositie 16 |
| d = –DAC |
want ADC is gelijkbenig |
| d = –DAC
< a |
het geheel is groter dan
het deel |
| b <
a |
|
|
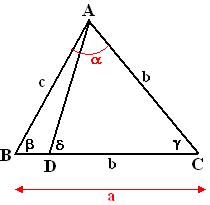 |
Maar dat is in tegenspraak
met b > a
dus kan niet gelden b < a
3. Aangezien beide vorige gevallen onmogelijk
zijn, blijft als enige mogelijkheid over dat b >
a |
|
|
| Propositie
20 is dan eindelijk de driehoeksongelijkheid.
Die zegt dat twee willekeurige zijden van een driehoek
samen altijd langer zijn dan de derde zijde. Ofwel: b
+ c > a |
|
|
 |
|
|
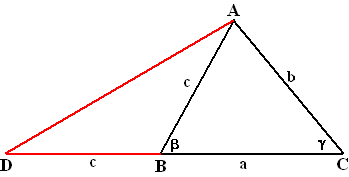
Verleng in driehoek ABC
zijde BC naar D zodat BD = AB = c
Dan is CD = CB + BD = a + c
–CAD > –BAD
(want het geheel is groter dan het deel)
–BAD = –BDA
= –CDA
In driehoek ADC is dus –CAD
> –CDA
Maar tegenover de grotere hoek ligt ook de grotere zijde
(propositie 19)
Dus is CD > AC ofwel a + c
> b
En daarmee is de driehoeksongelijkheid bewezen. |
|
|