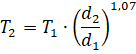VWO WC, 2017 - I   Pilot.

 

De formule van Riegel en kilometertijden .
       

De marathonloper Pete Riegel ontwikkelde een eenvoudige formule om te voorspellen welke tijd een hardloper nodig zou hebben om een bepaalde afstand af te leggen, op basis van zijn tijden op eerder gelopen afstanden.
Die formule luidt als volgt:
       

       

T1 is de tijd, uitgedrukt in seconden, die gelopen is op de afstand d1 en T2 is de voorspelde tijd in seconden op de afstand d2 . De formule is geldig voor afstanden vanaf 1500 meter tot en met 42195 meter, de marathon.
De formule is onafhankelijk van de gebruikte eenheden, dus d1 en d2 mogen bijvoorbeeld allebei in km worden ingevuld of allebei in m.

Harald loopt de 1500 meter in 4 minuten en 52 seconden.
       
3p.

1.

Bereken in minuten en seconden Haralds te verwachten tijd op de 10000 meter.
     

  

Het ligt voor de hand dat de gemiddelde snelheid lager wordt als de te lopen afstand groter wordt. Olaf loopt de 3000 meter in 8 minuten en 29 seconden. Dat is 509 seconden.
       
5p.

2.

Bereken met behulp van het bovenstaande en de formule van Riegel met hoeveel procent de gemiddelde snelheid van Olaf afneemt als de te lopen afstand verdubbelt.
     

  

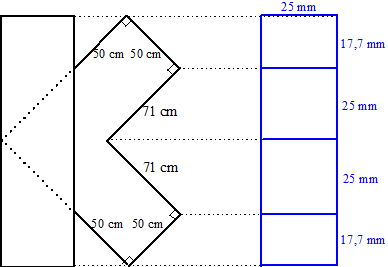
Een andere maat voor de snelheid is de kilometertijd K, het aantal seconden dat een hardloper gemiddeld per kilometer nodig heeft. In formulevorm:  K = T/d  .
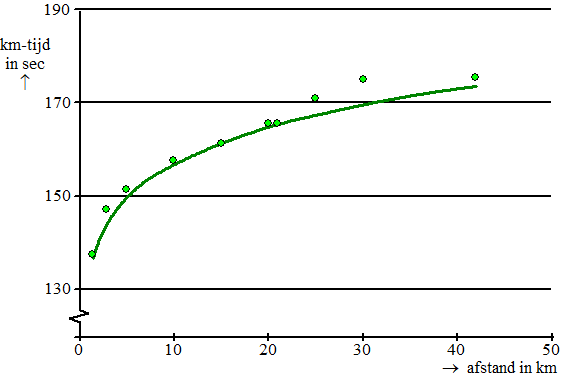
Hierbij is T de totale tijd in seconden en d de afstand in kilometers.

In de figuur hieronder zijn de kilometertijden weergegeven van de wereldrecords hardlopen zoals ze waren in november 2013.
 

 

De formule van de hier getekende grafiek die zo goed mogelijk bij de verschillende punten past, is van de vorm
K = a • d 0,07 . Hierbij is K de kilometertijd in seconden en d de afstand in kilometers.

Het wereldrecord op de 1,5 km (1500 meter) is precies 3 minuten en 26 seconden. Het bijbehorende punt ligt op de grafiek. Op basis hiervan kan berekend worden dat a ongeveer 133 is.
       
4p.

3.

 Bereken de waarde van a in twee decimalen nauwkeurig.
     

  
De kilometertijd van het wereldrecord op de 30 km ligt boven de kromme.
       
4p.

4.

Bereken hoeveel procent de kilometertijd op deze afstand hoger is dan de formule voorspelt.
     

   
Zonnepanelen.

     

Veel mensen denken erover om zonnepanelen aan te schaffen. Bedrijven spelen daarop in en geven daar allerlei informatie over op hun websites.
Op een dergelijke website tref je de volgende tekst aan:
       

Omdat de elektriciteitsprijs voortdurend stijgt, kan investeren in zonnepanelen interessant zijn. Laten we om te beginnen eens uitgaan van een stijging van de elektriciteitsprijs van 5% per jaar. Verder gaan we uit van een zonnepanelen-installatie met een opbrengst van 1750 kWh (kilowattuur) elektriciteit per jaar en een aanschafprijs van € 2995.
 

Op de website wordt uitgegaan van een zonnepanelen-installatie met een aanschafprijs van € 2995 en een opbrengst van 1750 kWh elektriciteit per jaar. Om de opbrengst in euro's te berekenen, wordt op diezelfde website gerekend met de prijs die de eigenaar van de zonnepanelen zou moeten betalen als hij de elektriciteit van een elektriciteitsbedrijf zou moeten kopen.
Er is gerekend met een prijs van € 0,225 per kWh elektriciteit voor het eerste jaar na aanschaf van de zonnepanelen en een jaarlijkse toename van de elektriciteitsprijs van 5%.
Voor de jaarlijkse opbrengst Z in euro's van de zonnepanelen in jaar t geldt nu de formule Z = 393,75 • 1,05t −1 .
Hierbij is t de tijd in jaren met t = 0 op het moment van aanschaf van de zonnepanelen.
       
3p.

5.

 Leg uit hoe je deze formule kunt afleiden uit de gegevens.
     

  

Om de jaarlijkse stijging van de elektriciteitsprijs van 5% te onderbouwen geeft de website elektriciteitsprijzen uit het verleden. Zo was in 1999 de prijs € 0,11 per kWh en in 2011 al € 0,22 per kWh. Als je aanneemt dat de elektriciteitsprijs in deze periode exponentieel gegroeid is, kom je echter niet op een (afgerond) jaarlijks groeipercentage van 5.
       
3p.

6.

Bereken het jaarlijks groeipercentage voor de periode 1999-2011. Rond je antwoord af op één decimaal.
     

  

Omdat het percentage waarmee de elektriciteitsprijs verandert, niet steeds hetzelfde is, staat er op de website een tool waarmee je dit percentage kunt wijzigen. Bij een lagere stijging van de elektriciteitsprijs zal de opbrengst in euro's per jaar van de zonnepanelen-installatie ook lager zijn.
       
4p.

7.

Bereken met welk percentage per jaar de elektriciteitsprijs minstens moet toenemen om in jaar 20 een opbrengst van de zonnepanelen-installatie van € 500 of meer te krijgen. Geef je antwoord in één decimaal nauwkeurig.
     

  

Voor het vervolg van deze opgave gaan we niet meer uit van een jaarlijkse stijging van de elektriciteitsprijs maar van een vaste prijs van € 0,225 per kWh.
In onderstaande tabel zie je een overzicht van de prijs en opbrengst van verschillende zonnepaneelsystemen van een ander bedrijf.
       
aantal panelen 8 12 18
aanschafprijs van het systeem € 4699 € 6299 € 8599
verwachte elektriciteitsopbrengst (kWh per jaar) 1667 2500 3750
       

De overheidssubsidie van 15% van de aanschafprijs is nog niet verwerkt in de prijzen van de tabel. De overheidssubsidie bedraagt maximaal € 650.

De terugverdientijd is de periode die het duurt tot het aankoopbedrag van het systeem is terugverdiend via besparing op de elektriciteitskosten.
In het begin van 2013 schafte iemand het systeem van 12 zonnepanelen aan met overheidssubsidie.
       
4p.

8.

Bereken, uitgaande van de verwachte elektriciteitsopbrengst, in welk jaar het aankoopbedrag volledig is terugverdiend.
     

  
       
Seine.
       

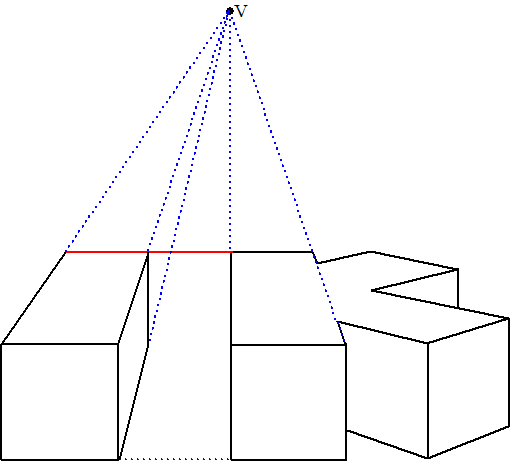
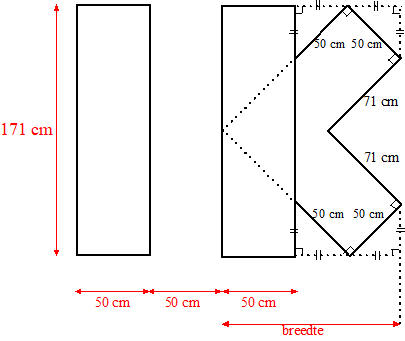
In de volgende figuur zie je het kunstwerk 'Seine' van Ellsworth Kelly, waarin de schittering op het water van de rivier de Seine verbeeld is door middel van zwarte en witte vakjes die allemaal even groot zijn.
       

       

Het paneel is ingedeeld in 83 (verticale) kolommen en 41 (horizontale) rijen. De meest linkse kolom is helemaal wit. In de kolom direct rechts daarvan bevindt zich 1 zwart vakje, de kolom daarnaast bevat één zwart vakje meer, enzovoort, totdat in de middelste kolom alle 41 vakjes zwart zijn. Er is maar één kolom met allemaal zwarte vakjes. Daarna bevat elke volgende kolom steeds één zwart vakje minder.
       

De zwarte vakjes in het kunstwerk zijn willekeurig geplaatst in de kolommen. Kelly heeft dit gedaan door te loten. Op deze manier zijn er veel verschillende eindresultaten mogelijk. Zelfs voor een kleiner kunstwerk van 9 kolommen en 4 rijen zijn er al veel verschillende mogelijkheden.
In figuur 2 staat een voorbeeld van 9 kolommen en 4 rijen die op de manier van Kelly van wit en zwart zijn voorzien: net als in het echte kunstwerk heeft de eerste kolom 0 zwarte vakjes, de tweede kolom één enzovoorts en de laatste kolom weer 0.
       

       
4p. 9. Bereken hoeveel verschillende 'kunstwerken' bestaande uit 9 kolommen en 4 rijen met deze procedure te maken zijn.
     

  

Om te berekenen hoeveel zwarte vakjes er in totaal zijn, kun je in gedachten alle zwarte vakjes in de kolommen naar beneden schuiven.
Zie de figuur hiernaast.
In een dergelijke figuur kun je het totale aantal zwarte vakjes bijvoorbeeld berekenen door de figuur op te delen in rechthoeken. In de figuur hieronder is in een figuur van slechts 9 vakjes breed en 4 vakjes hoog een rechthoek van 5 bij 4 getekend waarvan precies de helft van de vakjes donker is.
       
4p.

10.

 Bereken het totale aantal zwarte vakjes in het kunstwerk 'Seine'.
     

  

Rechthoeken waarvan de zijden een gulden-snede-verhouding hebben, worden vaak mooi gevonden. In figuur hiernaast zie je een rechthoek met korte zijde k en lange zijde l.

Voor een rechthoek met een gulden-snede-verhouding geldt altijd het volgende: de verhouding van de korte zijde k tot de lange zijde l is gelijk aan de verhouding van de lange zijde tot de korte en de lange zijde samen. In formulevorm: k : l = l : (k + l) .


Het kunstwerk 'Seine' heeft als afmetingen 41,9 cm bij 114,9 cm. Kelly heeft de zwarte en witte vakjes waaruit 'Seine' is opgebouwd niet vierkant maar rechthoekig gemaakt. In de volgende vraag gaat het erom of de afmetingen van zo'n vakje voldoen aan de gulden-snede-verhouding.
       
5p.

11.

Onderzoek of zo'n vakje van het kunstwerk 'Seine' een gulden-snede-verhouding heeft.
     

  

 

Experiment onder rechtenstudenten.
       

Bij een experiment onder 300 eerstejaars rechtenstudenten moesten deze studenten zich buigen over de volgende redenering:
       
   

Redenering I
‘Als je stoer bent, dan ga je laat naar bed.
Jij bent niet stoer, dus jij gaat niet laat naar bed.’
       

De bewering in de eerste zin kunnen we met symbolen als volgt weergeven:   S Þ L
       
3p.

12.

Geef de bewering in de tweede zin weer in logische symbolen en leg uit dat deze bewering niet volgt uit de bewering in de eerste zin.
     

  

Uit dit experiment bleek dat 70 procent van de 300 eerstejaars rechtenstudenten redenering I ontmaskerde als een ongeldige redenering.
De rechtenstudenten kregen de opdracht om ook bij de volgende redenering te onderzoeken of deze geldig of ongeldig was:
       
   

Redenering II
‘Als je een watje bent, dan ga je niet laat naar bed.
Jij gaat niet laat naar bed, dus jij bent een watje.’
       

Slechts 28 procent van de eerstejaars rechtenstudenten gaf het juiste antwoord. Eén van de volgende Venn-diagrammen is geschikt om te onderzoeken of redenering II geldig is of niet.
       

       
3p.

13.

Welk Venn-diagram is geschikt om te onderzoeken of redenering II geldig is of niet? Licht je antwoord toe.
     

  

Nu bekijken we de volgende twee beweringen:
  1. Als je stoer bent, dan ga je laat naar bed.
2. Als je een watje bent, dan ga je niet laat naar bed.
       
3p.

14.

Is uit dit tweetal beweringen de conclusie ‘Als je een watje bent, dan ben je niet stoer’ te trekken? Licht je antwoord toe.
     

  
IK - Kunstwerk.
       

Op de foto zie je een kunstwerk van Jan van Munster in de vorm van de letters I en K.

In de figuur hieronder staat een bovenaanzicht van dit kunstwerk op schaal 1:20.

Het kunstwerk is 50 cm hoog.
Je ziet hieronder enkele maten in cm staan van het kunstwerk. Die maten mag je gebruiken bij de volgende
vragen.

 

       

       
3p. 15.

Teken het rechterzijaanzicht van de letter K op schaal 1:20.
     

  

In de figuur is de breedte van de letter K aangegeven. Bovendien zijn in de letter K twee stippellijnen getekend.
Deze stippellijnen maken een rechte hoek met elkaar en het snijpunt ligt precies op de linker rand van de letter K. Er zijn ook nog enkele andere rechte hoeken gegeven. En zoals je ziet, zijn er 8 stukjes van even grote lengte bij de letter K. Je kunt nu aantonen dat elk van deze stukjes ongeveer 35,4 cm is en de breedte van de letter K van het kunstwerk ongeveer 121 cm is.
       
5p. 16.

Laat zien hoe die 35,4 cm en die 121 cm met deze gegevens berekend kunnen worden.
     

  
Hieronder is de letter K in perspectief getekend.
       

       
5p. 17. Teken de letter I op de juiste plaats erbij in deze tekening.
     

  

Jan van Munster heeft ook twee IK-paviljoens laten bouwen: twee expositiegebouwen in de vorm van de letters I en K. Zie de  foto hiernaast. Neem aan dat deze paviljoens een vergroting zijn van het IK-kunstwerk waarbij alle lengtes 8 maal zo groot zijn en dat de dikte van de wanden verwaarloosbaar is.

     
2p.

18.

Bereken de vloeroppervlakte van het paviljoen van de letter I in m2 nauwkeurig.
     

  

 

Pi in het oude India.
     

Indiase wiskundigen hebben in de loop van de geschiedenis een grote bijdrage geleverd aan de wiskunde. Ze hebben onder andere onderzocht hoe je het getal π kunt benaderen. In de zesde eeuw schreef de grote Indiase wiskundige Aryabhata het volgende:
     

Tel vier bij honderd op, vermenigvuldig vervolgens met acht en tel er dan
tweeënzestigduizend bij op. Het resultaat is bij benadering de omtrek van
een cirkel met diameter twintigduizend.
     
3p.

19.

Bereken, gebruikmakend van de formule omtrek cirkel  = π • diameter cirkel , in vier decimalen nauwkeurig welke waarde hieruit volgt voor het getal π .
   

  

Het is niet duidelijk hoe Aryabhata aan deze benadering gekomen is. In de 14e eeuw ontdekte de Indiase wiskundige Madhava een manier om de waarde van π te benaderen met behulp van een rij.
Hij begon met 4. Dat is groter dan π . Hij telde hier  -4/3 bij op. Het  resultaat 22/3 is nu kleiner dan π . Vervolgens telde hij bij het antwoord 4/5  op. Het resultaat  37/15  is nu weer groter dan π .
Hij ging zo verder, dus:

4 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + ...

Na elke nieuwe term die hij erbij optelde, kwam hij steeds dichter bij het  getal π . Zie de figuur.
         

Madhava kon bewijzen dat hij op deze manier inderdaad steeds dichter bij de werkelijke waarde van π kwam. Nadeel van deze manier is echter wel dat je veel termen nodig hebt voor een redelijke benadering van π . Het resultaat na drie termen: 37/15 verschilt nog behoorlijk van π .
         
3p.

20.

Bereken hoeveel termen je minimaal nodig hebt om te zorgen dat het verschil met π kleiner is dan 0,1.
       

  

Madhava telde voor zijn benadering van de termen van een rij bij elkaar

op, namelijk de termen van de volgende rij:   4/1,  -4/3,  4/5,  -4/7,  4/9,  -4/11
Hieronder staan twee mogelijke formules voor deze rij. Van deze formules is er één juist en de andere niet.
         
 

   
 

         
3p.

21.

 Onderzoek welke van deze twee formules de juiste is.
       

  

Madhava gaf ook een andere rij, die sneller tot een goede benadering van π leidde. De formule voor deze rij luidt:
         

         

Hiermee kon hij op soortgelijke wijze als boven een benadering van π vinden die steeds nauwkeuriger wordt naarmate meer termen gebruikt worden.
         
3p.

22.

Geef een benadering van π door de eerste drie termen van deze rij bij elkaar op te tellen en bereken het verschil met de werkelijke waarde van π in twee decimalen nauwkeurig.

  

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. 4 minuten en 52 seconden is 292 seconden
T2 = 292 • (10000/1500)1,07 = 2223 seconden
Dat is 37 minuten en 3 seconden.
   
2. d1 = 3000
T1 = 509
d2 = 6000
invullen in de formule:  T2 = 509 • (6000/3000)1,07 = 1068,611 seconden
v1 = 3000/509 = 5,8939
v2 = 6000/1068,611 = 5,6148
dat is  5,6148/5,8939 • 100% = 95,3%
Een afname van 4,7%
   
3. 3 minuten en 26 seconden is 206 seconden
T = 206  en  d = 1,5  dus  K =  206/1,5 = 137,33
137,33 = a • 1,50,07
137,33 = a • 1,0288
a = 137,33/1,0288 = 133,49
   
4. aflezen:  de kilometertijd is ongeveer 175 seconden.
133 • 300,07 =  168,75
175/168,75 • 100% = 103,7%
Dat is dus 3,7% hoger 
   
5. De prijs per Kwh heeft een toename van 5%, dat betekent een groeifactor van 1,05.
De beginwaarde is 0,225 dus de exponentiële formule zou worden  P = 0,225 • 1,05t 
Maar het beginjaar hoort nu bij t = 1 en niet bij t = 0
Dus moet je t vervangen door t  - 1:   P = 0,225 • 1,05t - 1 
De opbrengst is Z = 1750 • P = 1750 • 0,225 • 1,05t - 1  = 393,75 • 1,05t - 1
   
6. de groeifactor was 0,22/0,11 = 2  maar dat was in 12 jaar
g12 = 2  geeft  g = 21/12 = 1,059
Dat is een groeipercentage van 5,9%
   
7. Een opbrengst van 500 op t = 19 betekent  393,75 • g19 = 500
g19 = 500/393,75 = 1,2698
g = 1,26981/19 = 1,0127
Dat betekent een groei van 1,3%
   
8. de subsidie is 0,15 • 6299 = 944,85 dus dat wordt 650.
dan is de aanschafprijs  6299 - 650 = 5649
De opbrengst per jaar is  2500 • 0,225 = 562,50
Dat duurt dus  5649/562,50 = 10,04 jaar
Dus in 2023 is het volledig terugverdiend. 
   
9. 1e  + 9e kolom:  1 mogelijkheid
2e + 8e  kolom:  4 nCr 1 = 4 mogelijkheden
3e + 7e  kolom:  4 nCr 2 = 6 mogelijkheden
4e + 5e kolom:   4 nCr 3 = 4 mogelijkheden
in totaal 1 • 4 • 6 • 4 • 4 • 6 • 4 • 1 = 9216 mogelijkheden.
   
10. De eerste 41 kolommen geven  0 + 1 + 2 + ... +  40 = 820
De laatste 41 kolommen geven ook 820
De middelste kolom geeft 41
Samen 820 + 820 + 41 = 1681
   
11. De korte zijde is  41,9/41 = 1,022
De lange zijde is  114,9/83 = 1,384

1,022/1,384 = 0,738

1,384/(1,384 + 1,022) = 0, 575

Die zijn niet gelijk dus het is GEEN gulden snede.
   
12. niet stoer  Þ  niet laat naar bed
Ø S  Þ  Ø L
De eerste bewering zegt alleen iets over stoere mensen, en beweert duus helemaal niets over niet-stoere mensen.
   
13. Het is nog onbekend of jij een watje bent, dus "watje"  en "jij"  moeten deels overlappen.
Dat is dus diagram A.
   
14. Er staat:
S  Þ  L
W  Þ  ØL

De tweede is gelijk aan   Ø Ø L  Þ  ØW   ofwel  L  Þ  ØW
S  Þ  L en   L  Þ  ØW   betekent dat  S   Þ  ØW
Daaruit volgt weer   W  Þ  ØS

Dus JA.
   
15. Teken het gewoon aan de rechterkant.
Zie de blauwe figuur.
Voor het "echte" rechteraanzicht nog even een kwartslag draaien.
   
 16. onderaan staat een gelijkbenige rechthoekige driehoek met schuine zijde 50.
Als de rechthoekszijden beiden x zijn dan geldt  x2 + x2 = 502 = 2500
2x2 = 2500
x2 = 1250
x = √1250  = 35,4
 De totale breedte is dan 50 +  √1250 +  √1250 = 121 cm
   
17.
 		 Zie hieronder. de tekening wijst zichzelf wel, denk ik.
de twee rode lijntjes zijn even lang als het zwarte lijntje dat het verlengde ervan is.
 

   
18. De oppervlakte van de letter I is  1,71 • 0,50 = 0,855 m2
Als het paviljoen 8 keer zo groot is, is de oppervlakte ervan 64 keer zo groot.
64 • 0,855 = 55 m2
   
19. (100 + 4) • 8 + 62000 = 62832 is de omtrek
de diameter is 20000
 π = omtrek/diameter = 62832/20000 = 3,1416
   
20. gewoon proberen:
4/1 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + 4/13 - 4/15 + 4/17 = 3,252365... en dat is 0,11077... meer dan π
4/1 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + 4/13 - 4/15 + 4/17 - 4/19 = 3,041839... en dat is 0,09975 minder dan π
er zijn dus minimaal 10 termen nodig.
   
21. vul n = 1 in beide formules in.
formule I geeft  u1 = 4 • 1/1 = 4
formule II geeft  u1 =  1/1 = 1
Dus formule I is de juiste formule.
   
22. v0 = √12 • (-1)0/1 • 30 = √12
v1 = √12 • (-1) /3 • 3 =  -1/9√12
v2 = √12 • (-1)²/5 • 3² =  1/45√12
v0 + v1 + v2 = √12 • (1 - 1/9 + 1/45) = 3,156181472...
Dat scheelt 0,014588818...   dus ongeveer 0,01