VWO WC, 2016 - II   Pilot.
Vlinders.
       

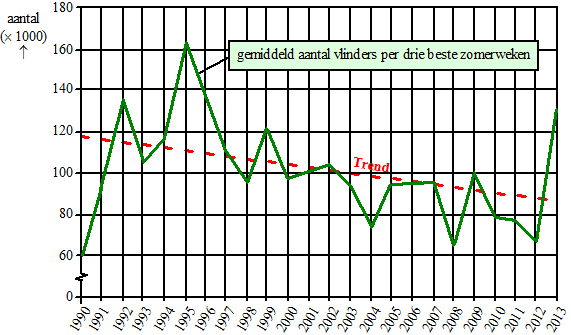
De zomer van 2013 was een topzomer voor vlinders. Toch gaat het aantal vlinders in Nederland volgens de Vlinderstichting langzaam achteruit. In dagblad Trouw stond in augustus 2013 de grafiek van onderstaande figuur .
       

       

In deze figuur is te zien dat het gemiddeld aantal vlinders in de drie beste zomerweken (dit zijn de drie weken met de meeste vlinders) een dalende trend vertoont. Deze trend wordt weergegeven door de gestippelde lijn. In de figuur is te zien dat 1995 zowel als 2013 goede vlinderjaren waren.
       

4p.

1.

Onderzoek of in 1995 het gemiddeld aantal vlinders in de drie beste zomerweken in procenten meer verschilde van het door de trendlijn voorspelde aantal dan in 2013.
       

5p.

2.

Stel een formule op voor de trendlijn van de figuur met t in jaren en t = 0 in 1995. Bereken daarmee in welk jaar er volgens deze trendlijn voor het eerst minder dan gemiddeld 60000 vlinders in de drie beste zomerweken zullen zijn.
     

 

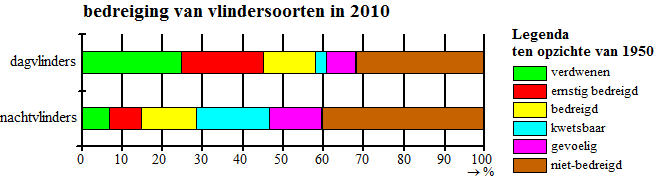
Het Centraal Bureau voor de Statistiek (CBS) publiceert regelmatig gegevens over de stand van zaken van de natuur in Nederland. In de figuur hieronder zie je een diagram waarin de mate van bedreiging is aangegeven van vlindersoorten in 2010. Uitgangspunt daarbij is het jaar 1950. Men beperkt zich daarbij tot soorten die in 1950 voorkwamen. Er is onderscheid gemaakt tussen soorten dagvlinders en soorten nachtvlinders. Je kunt in deze figuur bijvoorbeeld aflezen dat 24% van het totale aantal soorten dagvlinders sinds 1950 uit Nederland verdwenen is.
       

       

Hieronder staan twee mogelijke conclusies:
I.

Er zijn in 2010 meer niet-bedreigde soorten bij de nachtvlinders dan bij de dagvlinders.
II.

Het percentage ernstig bedreigde, bedreigde en kwetsbare soorten samen is in 2010 bij de dagvlinders groter dan bij de nachtvlinders.
       

3p.

3.

Geef van elk van deze twee conclusies aan of deze volgt uit bovenstaande figuur. Licht je antwoorden toe.
     

 

Om de bedreiging van soorten dagvlinders in Nederland te meten, gebruikt het CBS de volgende rekenmethode:
       
 

De totale bedreiging is de som van de volgende categorieën. Hierbij krijgen die categorieën de volgende gewichten:
verdwenen = 5, ernstig bedreigd = 4, bedreigd = 3, kwetsbaar = 2 en gevoelig = 1. De niet-bedreigde soorten krijgen gewicht 0.
       

In de tabel staat voor 1995 en 2006 de onderverdeling in de genoemde categorieën voor de soorten dagvlinders die in Nederland in 1950 voorkwamen.
       
  aantal dagvlindersoorten
jaar verdwenen ernstig  bedreigd bedreigd kwetsbaar gevoelig niet-bedreigd totaal
1995 17 5 11 7 2 29 71
2006 17 14 9 3 5 23 71
       

Voor soorten dagvlinders in 1995 resulteert de berekening van het CBS in een totale bedreiging van 154.
       

3p.

4.

Bereken met hoeveel procent de totale bedreiging voor soorten dagvlinders in 2006 is toegenomen ten opzichte van 1995.
     

 

De overheid wil dat de totale bedreiging teruggedrongen wordt. Men streeft ernaar dat voor dagvlinders de totale bedreiging 20% lager wordt dan in 1995.
       

4p.

5.

Geef een mogelijke verdeling waarbij afgerond de totale bedreiging 20% lager is dan in 1995 van de 71 dagvlindersoorten over de zes categorieën van de tabel. Ga er daarbij van uit dat het aantal verdwenen soorten gelijk gebleven is
       
Prille groei
       

Gemiddeld duurt een zwangerschap bij de mens 38 weken. Een ongeboren kind van 8 weken of ouder wordt een foetus genoemd.
In de volgende tabel staat het (gemiddelde) lichaamsgewicht G in gram van een foetus bij een leeftijd van t weken.
       
Leeftijd t in weken Lichaamsgewicht G in gram
8 4,7
10 21
15 160
20 480
25 990
30 1700
35 2700
38 3500
       

In deze opgave willen we onderzoeken welk model er bij deze tabel zou kunnen passen.
Het eerste model dat we bekijken is dat van exponentiële groei:

G = b • at  met a en b constanten.

Veronderstel dat de groei tussen week 8 en week 10 inderdaad exponentieel verloopt.
       

3p.

6.

Bereken met hoeveel procent per week het gewicht van de foetus dan toeneemt in die periode.
     

 

Exponentiële groei is echter geen goed model voor de groei van de foetus in de gehele periode van 8 tot 38 weken. Dit kun je afleiden uit de tabel.
       

3p.

7.

 Laat dat met een berekening zien.
     

 

Om een beter model voor de groei van de foetus te maken, berekenen we de logaritmes van de getallen in de vorige tabel.
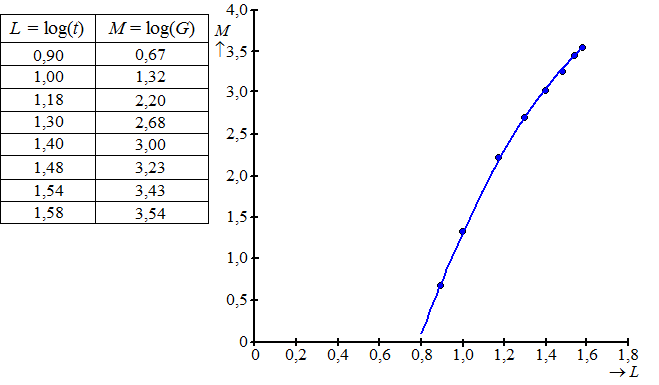
We bekijken dus de waarden van M = log (G) ten opzichte van L = log (t) . Zie de volgende tabel en de bijbehorende punten in de figuur ernaast.
       

       

De punten in de figuur liggen bij benadering op een bergparabool. Deze parabool is in de figuur getekend. Bij deze parabool hoort de volgende formule:

M = −7,131+11,305 • L − 2,892 • L2

Het gewicht van een foetus van 30 weken kan met deze formule worden berekend: bij t = 30 hoort L = log(30) ≈1,48 . Met de formule kun je de waarde van M en daarna de bijbehorende waarde van G berekenen.
Die waarde wijkt af van de waarde volgens de eerste tabel uit deze opgave.
       

3p.

8.

 Bereken hoeveel deze afwijking bedraagt.
     

 

Als de parabool van de figuur de groei goed beschrijft, dan zou de grafiek moeten stijgen gedurende de hele zwangerschap.
       

4p.

9.

Bereken de waarde van t waar de grafiek van M weer gaat dalen en leg uit dat dit voor het model geen bezwaar is.
     

 
Lampen.
       

Sinds enkele jaren is de handel in gloeilampen verboden. Het is de bedoeling dat iedereen overstapt op spaarlampen of LED-lampen. In deze opgave houden we ons met gloei-, spaar- en LED-lampen bezig.

Spaarlampen bestaan al sinds 1982, maar hebben nooit de populariteit van de gloeilamp kunnen bedreigen. Toch is een gloeilamp op de lange termijn een stuk minder voordelig dan een spaarlamp: de levensduur van een gloeilamp is veel korter dan die van een spaarlamp én een gloeilamp gebruikt vijf keer zoveel energie als een spaarlamp om dezelfde lichtsterkte te produceren.
Het energieverbruik per tijdseenheid van lampen (het wattage) wordt uitgedrukt in watt (W). Er geldt dus dat een gloeilamp een vijf keer zo hoog wattage heeft als een spaarlamp die evenveel licht geeft. Zie ook de tabel.
       
Vergelijking gloei- en spaarlamp van dezelfde lichtsterkte
  levensduur wattage aanschafprijs
gloeilamp 1300 uur 75W € 0,50
spaarlamp 7800 uur 15W € 6,50
       

De prijs van elektriciteit is €0,23 per kWh (kilowattuur). Dat wil zeggen dat het gebruik van 1 kW (= 1000 W) gedurende 1 uur €0,23 kost.
Bijvoorbeeld: een lamp met een wattage van 100 W die drie uur brandt, zal  100/1000 • 3 • 0,23 ≈ €0,07  aan elektriciteit kosten.

De gebruikskosten van lampen bestaan uit de aanschafkosten en de kosten om ze te laten branden. Een spaarlamp van 15 watt zal tijdens zijn gehele levensduur van 7800 uur een stuk goedkoper zijn dan het gebruik van meerdere gloeilampen met dezelfde lichtsterkte die samen 7800 branduren hebben.
       

5p.

10.

Bereken hoeveel goedkoper de spaarlamp is. Geef je antwoord in centen nauwkeurig.
     

 

Stella heeft een spaarlamp gekocht van 12 W. Deze lamp kostte € 8,40.
Een gloeilamp van 60 W, dus met dezelfde lichtsterkte, kost € 0,60. De spaarlamp is al goedkoper bij een aantal branduren dat kleiner is dan de levensduur van één gloeilamp met dezelfde lichtsterkte.
       

4p.

11.

Onderzoek na hoeveel branduren de gebruikskosten van de spaarlamp lager zijn dan die van één gloeilamp.
     

 

De laatste jaren is de LED-lamp steeds populairder aan het worden. Deze lampen zijn nóg zuiniger dan spaarlampen en gaan bovendien nog veel langer mee.

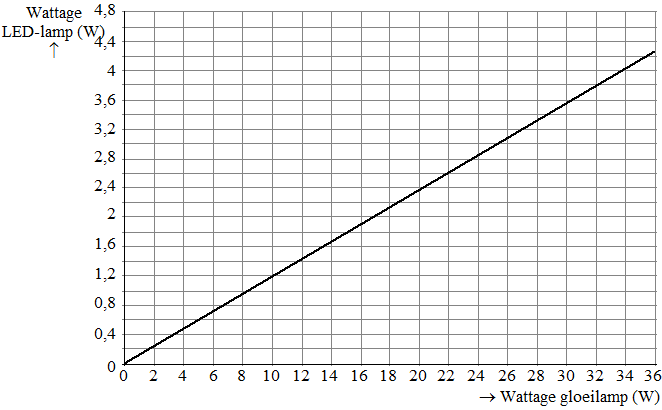
In de grafiek is het verband getekend tussen het wattage van gloeilampen en het wattage van LED-lampen met dezelfde lichtsterkte.
       

       

Het is duidelijk dat een LED-lamp een veel lager wattage heeft dan een gloeilamp die dezelfde hoeveelheid licht geeft. Het verschil is zo groot dat je kunt inzien dat een LED-lamp een lager wattage heeft dan een spaarlamp die dezelfde hoeveelheid licht geeft.
       

4p.

12.

Bereken hoeveel procent meer wattage een spaarlamp nodig heeft, vergeleken met een LED-lamp die dezelfde hoeveelheid licht geeft.
     

  

 

IQ-test.
       

Bij onderzoeken naar het vermogen tot logisch redeneren, zoals bijvoorbeeld in een IQ-test, worden vaak onzinnige uitspraken gebruikt die de kandidaat als waar aan moet nemen. Dit wordt gedaan, opdat de antwoorden op de vragen niet op basis van de werkelijkheid, maar op basis van logica gegeven worden. De volgende vraag komt uit zo’n test.

Ga ervan uit dat de volgende drie uitspraken waar zijn.
       

 1.   Alle vrouwen worden op den duur kaal.
 2.   Alle vrouwen houden van alle mannen.
 3.   Alle mannen houden van winkelen.
       

4p.

 13.

Geef van elk van de vier onderstaande beweringen aan of deze wel of niet uit de bovenstaande uitspraken volgt. Licht elk van je antwoorden toe.

Bewering a: Iemand die kaal is, is geen man.
Bewering b: Als iemand niet kaal wordt, dan is het geen vrouw.
Bewering c: Kale vrouwen houden van winkelen.
Bewering d: Vrouwen houden van mannen die van winkelen houden.
       

We voeren de volgende afkortingen in:

M: De persoon is een man.
W: De persoon houdt van winkelen.
K: De persoon is kaal.
       

3p.

14.

Schrijf de bewering “als een vrouw kaal is, dan houdt ze van winkelen” op in logische symbolen. Gebruik daarbij alleen de bovenstaande afkortingen.
       

We bekijken de volgende logische bewering:   ¬K ⇒ W

Deze bewering volgt niet uit de drie uitspraken aan het begin van de opgave. Hieronder staan twee extra uitspraken:
       

 4   Alle mannen hebben haar.
 5   Vrouwen die van mannen houden, houden van winkelen.
       

Als één van deze twee extra uitspraken toegevoegd wordt aan het lijstje uitspraken 1, 2 en 3 dan volgt
de bewering ¬K ⇒ W wel uit dat lijstje uitspraken.
       

3p.

15.

Beredeneer welke van deze twee uitspraken moet worden toegevoegd aan het lijstje uitspraken.
       
Serigrafia.
       

De kunstenaar Max Bill paste geometrie toe in zijn werk. Het kunstwerk Serigrafia heeft hij in 1979 gemaakt.

       

       

We gaan kijken hoe dit kunstwerk is opgebouwd.

Hieronder zie je figuur 1, de startfiguur (n = 1). Deze figuur bestaat uit 4 rechthoeken1 van 1 bij 1 cm. Figuur 2 (n = 2) bestaat uit de rechthoeken van figuur 1, uitgebreid met 4 rechthoeken van 2 bij 1 cm.
Figuur 3 (n = 3) bestaat uit de rechthoeken van figuur 2, uitgebreid met 4 rechthoeken van 3 bij 1 cm. Op deze manier zou je het kunstwerk onbeperkt uit kunnen breiden.

In het midden van de figuren zie je steeds een draaipunt getekend. Als je niet op de kleuren let en de figuur over 90° draait, krijg je weer dezelfde figuur.
       

       

3p.

16.

Teken  het rechterbovendeel van figuur 5, het kwart dus dat bij de pijl hoort.
       

Als het figuurnummer, n dus, groter wordt, wordt het bijbehorende aantal rechthoeken (inclusief vierkanten) in een figuur ook groter.
       

3p.

17.

 Bereken bij welk figuurnummer n het aantal rechthoeken gelijk is aan 112.
       

Voor de oppervlakte (in cm2) van figuur n geldt de volgende formule:

Oppervlakte = 4(1 +  2  +  3 + ... +  n)
       

5p.

18.

Toon aan dat deze formule juist is en bereken de oppervlakte van figuur 8.
       

Nu gaan we kijken naar de kleuren die in Serigrafia gebruikt zijn.
Begin bij het oranje vierkantje links en draai met de wijzers van de klok mee. Je telt dan 8 verschillende kleuren (van oranje  tot en met lichtgroen). Max Bill heeft ervoor gezorgd dat die kleuren zich telkens in dezelfde volgorde herhalen totdat je alle 24 rechthoeken tegengekomen bent.

Je zou, op dezelfde manier werkend als Max Bill, die kleuren van de "eerste 8 rechthoeken" ook in een andere volgorde hebben kunnen plaatsen. Door de kleuren in volgorde te variëren, zou je heel veel verschillende kunstwerken kunnen maken.
       

3p.

19.

Bereken hoeveel verschillende kunstwerken er van Serigrafia kunnen zijn.
       
Banken in Groningen.
       

In Groningen staat een kunstwerk dat gemaakt is uit twee even grote rechthoekige banken waarvan de bovenkanten op gelijke hoogte liggen. Zie de foto.

De hoek tussen de twee banken is recht (90°). Dit kun je ook in het onderstaande bovenaanzicht zien.
       

       

       
De figuur hieronder geeft een tekening van deze situatie.
In deze figuur  is ook een lijn getekend die de horizon voorstelt.
       
       

3p.

20.

Leg met behulp van het tekenen van hulplijnen in deze tekening uit dat de getekende lijn inderdaad de horizon is die bij deze tekening hoort.
       

Een andere kunstenaar is van mening dat het kunstwerk wel wat aanvulling kan gebruiken en wil graag de voorste bank verlengen met een vierkant betonnen tafeltje dat net zo hoog is als de banken en precies past tegen de linkerzijkant van de voorste bank. Het tafeltje is dus net zo breed als de zijde a (zie foto) van de bank.
       

5p.

21.

Teken in dezelfde figuur de bovenkant van dit tafeltje erbij.
       

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. in 1995 geeft de grafiek 165 en de trendlijn 111
Dat is een afwijking van 54 en dat is  54/111 • 100% = 49%

in 2013 geeft de grafiek 130 en de trendlijn 86
Dat is een afwijking van  44 en dat is 44/86 • 100% = 51%

De afwijking is procentueel in 2013 het grootst.
   
2. Lees twee punten af,  bijvoorbeeld  (8, 100) in 2003  en  (0, 111)  in 1995
a =  Δy/Δx =  (111000 - 100000)/(0 - 8) = -1375
b = 111000 want dat is op y = 0
A = 111000 - 1375t

111000 - 1375t = 60000
1375t = 51000
t = 51000/1375 = 37 dus dat is in 2032
   
3. conclusie I:
in 2010 zijn er bij de nachtvlinders  100 - 60 = 40% niet-bedreigde soorten
in 2010 zijn er bij de dagvlinders 100 - 68 = 32% niet-bedreigde soorten
Conclusie I klopt wel.

conclusie II:
in 2010 is dat percentage bij de dagvlinders 61 - 25 = 36%
in 2010 is dat percentage bij de nachtvlinders 47 - 7 = 40%
Conclusie II klopt niet.
   
4. dagvlinders in 2006:   17 • 5 + 14 • 4 + 9 • 3 + 3 • 2 + 5 • 1 + 23 • 0 = 179
De toename is dan  179 - 154 = 25
Dat is  25/154 • 100% = 16,2 %
   
5. de bedreiging moet dan  0,80 • 154 = 123 worden
verdwenen levert al een bijdrage van 17 • 5 = 85
dus de overige categorieën moeten bijdrage 38 leveren.
Tja, dat kan op veel manieren. Maar die 38 moet wel met in totaal 54 soorten bereikt worden.
Een voorbeeld:
 
verdwenen ernstig bedreigd bedreigd kwetsbaar gevoelig niet-bedreigd
17 3 3 5 7 36
   
6. in twee weken is de groeifactor  21/4,7 = 4,468
voor de g per week geldt dus  g2 = 4,468  dus  g = 4,4680,5 = 2,11
dat is een toename van 111% per week
   
7. bijvoorbeeld:
tussen week 10 en 15 is de groeifactor  160/21 = 7,62
tussen week 30 en 35 is de groeifactor 2700/1700 = 1,59
Dat is niet gelijk, terwijl de tijdsverschillen wel gelijk zijn (5 weken) dus de groei is niet exponentieel.
   
8. L = 1,48 geeft  M = -7,131 + 11,305 • 1,48 - 2,892 • 1,482 = 3,27
log(G) = 3,27 geeft  G = 103,27 = 1862 gram
In de tabel staat 1700 gram dus dat scheelt 162 gram.
   
9. de grafiek gaat weer dalen bij de top van de parabool, en dat is bij  -b/2a = -11,305/(2 • -2,892) = 1,95
(kan ook met GR en calc - maximum)

Dan is  log(t) = 1,95  dus  t = 101,95 ≈ 89  weken.
Maar zo lang duurt een zwangerschap nooit.
   
10. spaarlamp: 6,50 + 15/1000 • 7800 • 0,23  = €33,41

één gloeilamp:  0,50 + 75/1000 • 1300 • 0,23 = 22,925
Er zijn 7800/1300 =  6 gloeilampen nodig, dus dat is samen  €137,55

Dat scheelt  €104,14
   
11. na x uren heeft een spaarlamp  8,40 + 12/1000 • 0,23 • x  = 8,40 + 0,00276x  gekost
na x uren heeft een gloeilamp 0,60 + 60/1000 • 0,23 • x = 0,60 + 0,0138x gekost.
Dat is gelijk als  8,40 + 0,00276x  = 0,60 + 0,0138x
7,80 = 0,01104x
x = 7,80/0,01104 = 706,5...
Vanaf 707 uren zal de spaarlamp goedkoper zijn.
   
12. bij een gloeilamp van 22W hoort een spaarlamp van 2,6W
Als je een gloeilamp van 22W hebt, dan geeft een spaarlamp van 22/5 = 4,4W even veel licht.
4,4/2,6 = 1,69
Dat is dus 69% meer.
   
13. a.  NIET. er staat nergens iets over kaalheid bij mannen.
b.  WEL uit uitspraak 1:   vrouw ⇒ kaal is dezelfde uitspraak als  niet-kaal ⇒ niet-vrouw
c.  NIET.  Er staat nergens iets over het winkelen van vrouwen.
d.   WEL. Als vrouwen van alle mannen houden, dan houden ze ook van alle mannen die graag winkelen .
   
14. "kale vrouwen"  betekent  "niet-man EN kaal",  dus   (¬ M ∧ K)
Daaruit moet W volgen, dus dat wordt:   (¬ M ∧ K) ⇒ W
   
15. ¬ K ⇒ W  betekent:  iemand die niet kaal is houdt van winkelen.
van de mannen is het al bekend dat ze van winkelen houden:  dat is aanname 3.
dus moeten we er nog voor zorgen dat ook alle vrouwen van winkelen houden
dat kan met aanname 5:  als vrouwen die van mannen houden ook van winkelen houden, dan geldt dat voor alle vrouwen immers alle vrouwen houden van mannen  (aanname 2)
aanname 5 moet erbij.
   
16. De rechtopstaande rechthoek van 5 bij 1 moet direct rechts aan de  opstaande lijnen komen .
De rest volgt vanzelf:
 

   
17. De aantallen rechthoeken zijn achtereenvolgens:  4 - 8 - 12 - 16 -
Het aantal is dus 4n
4n = 112 geeft   n = 28
   
18. Er zijn van elke grootte steeds 4 rechthoeken.
dus 4 van 1 bij 1
4 van 2 bij 1
4 van 3 bij 1
.....
4 van n bij 1
De oppervlakte is dan 4 • 1 • 1 + 4 • 2 • 1 + 4 • 3 • 1 + .... + 4 • n • 1
Dat is  4 • (1 + 2 + 3 + ... + n
   
19. Voor de eerste zijn 8 mogelijkheden, voor de tweede nog 7, voor de derde 6, enz.
Na acht keuzes ligt de rest vast.
die acht keuzes kunnen op 8 • 7 • ... • 1 = 8! = 40320 manieren.
   
 
20.
  de blauwe lijnen zijn de evenwijdig lopende tafelranden en snijden elkaar in V1 op de horizon
de rode lijnen zijnde diagonalen van de vierkanten uit het bovenaanzicht en snijden elkaar in V2 op de horizon.
   
21.  
  verleng de rode lijn vanaf V2 en snij die met de voorrand van de voorste bank, Dat geeft een vierkant want deze lijn maakt een hoek van 45º met de voorrand.
De rest van de tekening spreekt voor zichzelf.