VWO WC, 2015 - I
Succesvogels en Pechvogels.
       
In 2010 heeft Chris van Turnhout onderzoek gedaan naar de ontwikkeling van de aantallen broedvogels in Nederland gedurende de periode 1990 − 2005. Hij onderzocht welke eigenschappen bepalen of een vogelsoort in aantal toeneemt (‘succesvogels’) of afneemt (‘pechvogels’).
       

       
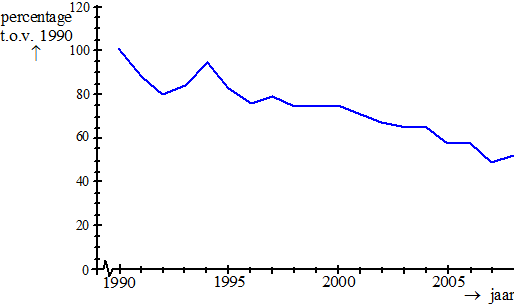
Deze figuur gaat over een ‘pechvogel’: de grutto. Langs de verticale as staan de aantallen als percentage van het aantal grutto’s dat er in 1990 was. In 2004 waren er 60000 grutto’s. Met behulp van dit gegeven en gegevens uit deze figuur kun je nu het aantal grutto’s in 1994 berekenen.
       
3p. 1. Bereken het aantal grutto’s in 1994.
     

   
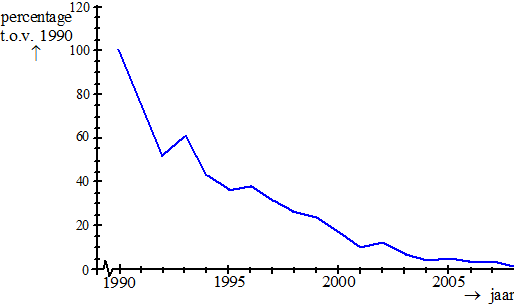
In de periode 1990 − 2005 nam het aantal kuifleeuweriken dramatisch af, zoals in de volgende figuur goed te zien is.
       

       
In 2005 was er nog slechts 5% over van het aantal in 1990. Ga ervan uit dat het aantal exponentieel afnam in deze periode.
       
4p. 2. Bereken de groeifactor per jaar voor de kuifleeuwerik. Ga uit van de gegevens van 1990 en 2005.
     

   
Uit het onderzoek is gebleken dat de plaats van het nest belangrijk is voor de mate van succes van een vogelsoort. Een soort A die zijn nest in struiken maakt, groeit exponentieel met groeifactor 1,042 per jaar. En een soort B die in bomen nestelt, groeit exponentieel met groeifactor 1,016 per jaar.
Neem aan dat de aantallen van deze twee broedvogelsoorten op een bepaald moment gelijk zijn.
       
4p. 3. Bereken na hoeveel gehele jaren het aantal vogels van soort A voor het eerst meer dan twee keer zo groot is als dat van soort B.
     

   
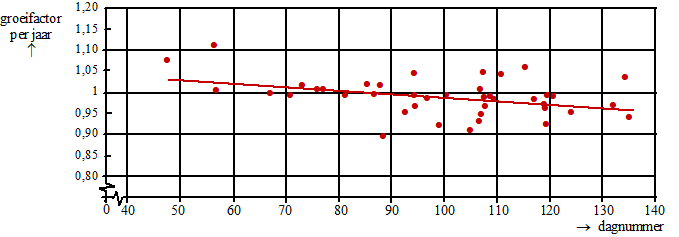
Een eigenschap die belangrijk is voor het succes van trekvogels is de datum van aankomst in Nederland.
In onderstaande figuur zie je het verband tussen de groeifactor per jaar en de dag van aankomst in Nederland. Deze dag is aangegeven met een dagnummer: dag 33 is 2 februari, dag 34 is 3 februari, enzovoort.
De 41 onderzochte vogelsoorten zijn met punten aangegeven. In deze figuur is de best passende lijn bij deze 41 punten getekend. Deze lijn geeft aan dat in het algemeen geldt: hoe later een soort aankomt in Nederland, hoe kleiner de groeifactor van die soort.
       

       
Vergelijk drie denkbeeldige soorten die precies op de lijn van deze figuur liggen. Soort X komt op dag 120 aan, soort Y op dag 130 en soort Z op dag 140. Omdat ze steeds met 10 dagen verschil aankomen, is het verschil in groeifactor ook constant: ze liggen immers op een rechte lijn. Aankomen op dag 120 levert, zo is vast te stellen, een groeifactor van 0,975. En aankomen op dag 130 levert een groeifactor van 0,965.

De vraag is of het verschil in halveringstijd (dat is de tijd die het duurt tot er nog 50% van het aantal over is) bij deze drie soorten ook constant is.
       
5p. 4. Onderzoek door het berekenen van de halveringstijden van de soorten X, Y en Z of de halveringstijd ook met een vast aantal jaren afneemt.
     

   
Statistiek in de auto-industrie.
       
Bij een productieproces worden voortdurend controlemetingen uitgevoerd. Bijvoorbeeld bij de productie van slangen voor achterruitsproeiers mag de lengte van de slang niet al te veel afwijken van de streefwaarde. Die lengte van de slang moet binnen bepaalde specificatiegrenzen blijven.

Slangen van achterruitsproeiers
De streefwaarde van de lengte van de slang voor de achterruitsproeier van een bepaald type auto is 280 cm. In werkelijkheid zullen niet alle slangen precies 280 cm lang zijn. De lengte van de slang moet liggen tussen de specificatiegrenzen 276 en 284 cm. Als de lengte van de slang hierbuiten valt, dan wordt de slang afgekeurd.
       
Het productieproces wordt zo ingericht, dat het percentage dat buiten de specificatiegrenzen valt, erg klein is. In de figuur hiernaast zie je hier een voorbeeld van: de lengte van de geproduceerde slangen is gemiddeld 280 cm met een standaardafwijking van 0,65 cm. Hierbij is het gemiddelde dus de streefwaarde. Neem hierbij aan dat de lengte van de geproduceerde slangen normaal verdeeld is

       
3p. 5. Bereken hoeveel procent van de geproduceerde slangen een lengte heeft die meer dan 2 cm afwijkt van de streefwaarde.
     

   
Het is mogelijk dat er iets mis is met het productieproces. In de figuur hiernaast is de situatie weergegeven dat de gemiddelde lengte van de geproduceerde slangen groter is dan de streefwaarde 280 cm. Neem aan dat de standaardafwijking niet veranderd is.
We kijken nu naar het percentage van de geproduceerde slangen met een lengte groter dan 284 cm.

       
4p. 6. Bereken vanaf welk gemiddelde dit percentage groter is dan 5%. Rond je antwoord af op gehele cm.
     

   
Om vast te stellen of het productieproces van slangen voor achterruitsproeiers nog goed verloopt, neemt men regelmatig een steekproef uit de geproduceerde slangen. Hierbij bepaalt men het steekproefgemiddelde g en berekent men de procescapaciteitsmaat C.
Er geldt:

       
Hierin is g het steekproefgemiddelde. We nemen aan dat s, de standaardafwijking van het proces, constant is en steeds gelijk is aan 0,65. De procescapaciteitsmaat C is de kleinste van deze twee waarden Clinks en Crechts. Als bijvoorbeeld het steekproefgemiddelde g  gelijk is aan 281 cm en s = 0,65,  dan geldt:

Hieruit volgt dat in dit voorbeeld geldt:  C = Crechts ≈  1,5.

We nemen verder aan dat het steekproefgemiddelde g binnen de specificatiegrenzen ligt. De standaardafwijking s verandert ook nu niet.

Het productieproces verloopt slechter als het steekproefgemiddelde g verder van de streefwaarde af komt te liggen.
       
4p. 7. Beredeneer aan de hand van de formules of de waarde van C in dit geval groter wordt of juist kleiner.
     

   
Koplampen.
       
Ook de koplampen van een auto moeten aan strenge eisen voldoen. De koplampen moeten tussen 0º en 2,5º naar beneden wijzen, zodat tegenliggers niet verblind worden. Neem voor de volgende vraag aan dat er niets mis is met het productieproces en dat de hoek van een koplamp normaal verdeeld is met gemiddelde 1,25º en standaardafwijking 0,25º. Men neemt een steekproef van 50 koplampen en men meet hierbij de hoeken op.
       
5p. 8. Bereken de kans dat van de hoeken van deze 50 koplampen er één of meer niet tussen 0,5º en 2,0º liggen.
     

   
In onderstaande figuur zie je de grafiek met de hoeken van 50 koplampen uit een andere steekproef. De streefwaarde 1,25º is in de grafiek te zien als een horizontale lijn.
       

       
Alle koplampen in deze figuur voldoen aan de eisen. Toch is er een aanwijzing dat er iets niet helemaal in orde is met het productieproces: in de grafiek liggen meer waarden boven, namelijk 34, dan onder de 1,25º. Neem aan dat de gemiddelde hoek in het productieproces 1,25º is. Elke koplamp heeft dan evenveel kans om boven of onder de waarde 1,25º te liggen.
       
4p. 9. Bereken in dat geval de kans dat bij 34 of meer van de 50 koplampen de hoek groter is dan 1,25º.
     

    

 

Reistijden.
       
In 2010 stond in NRC Handelsblad een artikel waarin de prestaties van vliegtuig, hogesnelheidstrein (hst) en gewone trein met elkaar vergeleken werden. Bij het artikel stond onderstaande figuur. In deze figuur staat horizontaal de reisafstand in kilometers en verticaal de totale reistijd van-deur-tot-deur in uren. De reistijd van-deur-tot-deur is de totale tijd die nodig is voor de trein- of vliegreis zelf en voor de verplaatsingen van en naar het station of vliegveld.
       

       
Uit de figuur blijkt dat men voor reizen met een afstand van meer dan 100 km bij elk vervoermiddel uitgaat van een constante snelheid.
       
3p. 10. Bereken deze snelheid voor de hogesnelheidstrein in km/u.
     

   
Boven de grafiek in de figuur staat bij de bovenste pijl: ‘gewone trein sneller dan vliegtuig’. Ook bij de onderste pijl hoort een dergelijke uitspraak te staan. Hier volgt een drietal mogelijkheden:
  1. De gewone trein is sneller dan de hst
  2. De hst is sneller dan de gewone trein
  3. De hst is sneller dan het vliegtuig en sneller dan de gewone trein
       
4p. 11. Beredeneer voor elk van de drie uitspraken met behulp van de figuur of de uitspraak juist is.
     

   
Voor een reis met de auto is er geen reistijd van en naar een station of vliegveld. Neem daarom aan dat we bij autoreizen ook bij afstanden beneden de 50 km uit mogen gaan van een constante snelheid.
       
3p. 12. Teken in de figuur op de uitwerkbijlage de grafiek van het reizen met de auto met een snelheid van 100 km/u en bepaal daarmee tot welke afstand de auto sneller is dan het vliegtuig.
     

   
Naar aanleiding van de figuur heeft men de volgende formules opgesteld. Hierbij is a de afstand in km en r de reistijd in uren: 
  Vliegtuig:     r = 0,00137a + 3,43
  Gewone trein:    r = 0,00793a + 1,10
       
3p. 13. Onderzoek met behulp van deze formules vanaf welke afstand de reistijd met het vliegtuig kleiner is dan de reistijd met de gewone trein.
     

    
Bevingen in Japan.
       
De laatste jaren waren de zeebevingen in de buurt van Japan regelmatig in het nieuws. De zeebeving van Sendai in 2011 en de aardbeving van 2004 die een enorme tsunami in de Indische Oceaan veroorzaakte, zijn allebei bevingen met een kracht van 9,0 of meer op de schaal van Richter. De Amerikaan Charles Richter gebruikte seismogrammen om de magnitude (kracht) van een beving te kunnen bepalen. In de figuur zie je een voorbeeld van een seismogram. In dit seismogram zie je de gemeten trillingen van de aarde als uitwijkingen in mm. De grootste uitwijking in het seismogram heet de maximale amplitude.
       
       
Om de magnitude van een beving te bepalen, gebruikt men de formule van Richter. Hieronder staat een vereenvoudigde versie daarvan:
  M = log(A) + 3
In deze formule is M de magnitude en A de maximale amplitude in mm.

Uit de formule blijkt, dat als de maximale amplitude A tien keer zo groot wordt, de magnitude met 1 eenheid toeneemt.
       
3p. 14. Toon met behulp van de rekenregels voor logaritmen aan dat  log(10A) + 3 altijd 1 groter is dan log(A) + 3.
     

  
Met de formule M = log(A) + 3 kan M berekend worden als A bekend is.
Men kan echter ook A berekenen als M bekend is. Dat kan met de formule  A = 0,001 • 10M.
Deze laatste formule is af te leiden uit de formule M = log(A) + 3.
       
3p. 15. Toon dit aan.  
     

  
Een van de naschokken van de beving van 2004 had een magnitude van 5,3 op de schaal van Richter. En bij de beving van 2011 was er een naschok met een magnitude van 5,0. In een wetenschappelijk tijdschrift stond dat de maximale amplitude op het seismogram bij de naschok van 2011 gelijk was aan 102,0. De maximale amplitude tijdens de naschok van 2004 was groter dan die van 2011.
       
3p. 16. Bereken hoeveel keer zo groot.  
     

  
De zeebeving van 11 maart 2011 met de daaropvolgende tsunami zorgde voor grote problemen bij de kerncentrale Fukushima I. Om de reactoren te koelen, werd zeewater in de reactoren gepompt. Dit water lekte, radioactief geworden, weer terug in zee. Hierdoor raakte vis besmet met radioactief jodium en moest de visvangst tijdelijk worden stopgezet.

Radioactief jodium verdwijnt volgens een exponentieel proces. De halveringstijd van radioactief jodium is 8 dagen. Op 6 april 2011 gaven metingen aan dat er 4800 keer de maximaal toegestane hoeveelheid radioactief jodium in het zeewater aanwezig was. De maximaal toegestane hoeveelheid radioactief jodium is 5 becquerel/liter. Op het moment dat de maximaal toegestane hoeveelheid werd bereikt, mocht er weer gevist worden. We gaan ervan uit dat er na 6 april 2011 geen nieuw radioactief jodium meer in zee lekte.
       
5p. 17. Bereken na hoeveel dagen er weer gevist mocht worden.
     

  

 

De Manchester kleurencirkel.
       
Onderzoekers van de Universiteit van Manchester hebben onderzocht of er verschillen zijn in kleurvoorkeuren tussen gezonde en depressieve proefpersonen. Proefpersonen kregen een cirkel met daarin verschillende kleuren te zien. De onderzoekers vroegen aan hen welke kleuren ze positief beoordeelden en welke kleur het beste paste bij hun stemming van de laatste paar maanden.

Om de kleuren te registreren, had men kunnen kiezen voor het RGB-kleursysteem. Dat is een manier om een kleur uit te drukken met behulp van een combinatie van de drie hoofdkleuren Rood-Groen-Blauw. De hoeveelheid van elk van deze hoofdkleuren die nodig is om de mengkleur te verkrijgen, wordt uitgedrukt in een geheel getal dat kan variëren van 0 tot en met 255. Elke verschillende combinatie van die drie getallen geeft een andere kleur. Zo geeft (255,255,0) een bepaalde kleur geel.
       
3p. 18. Bereken hoeveel verschillende kleuren er op deze manier aangeduid kunnen worden.
     

  
De onderzoekers gebruikten een ander systeem. Ze kozen negen hoofdkleuren: rood, groen, bruin, geel, paars, roze, blauw, oranje en grijs. Van elke hoofdkleur gebruikten ze vier tinten: zeer donker, donker, licht en zeer licht. Bovendien gebruikten ze zwart en wit. In totaal gebruikten ze dus 38 kleuren, die ze de nummers 1 tot en met 38 gaven.

In het eerste deel van het onderzoek vroeg men gezonde proefpersonen deze kleuren te beoordelen, waarbij ze per kleur konden kiezen uit positief, neutraal of negatief. De resultaten staan in de volgende tabel. Hierin kun je bijvoorbeeld aflezen dat kleur nummer 1 (zeer donkerrood) door 3% van de proefpersonen als positief werd aangemerkt en door 24% van de proefpersonen als negatief.
       
  zeer donker donker licht zeer licht
  nr P
(pos)
%		 N
(neg)
%		 nr P
(pos)
%		 N
(neg)
%		 nr P
(pos)
%		 N
(neg)
%		 nr P
(pos)
%		 N
(neg)
%
rood 1 3 24 2 9 14 3 36 19 4 25 13
groen 5 8 22 6 31 7 7 29 6 8 33 4
bruin 9 0,5 54 10 0,5 44 11 0,5 29 12 2 9
geel 13 47 0,5 14 72 0,5 15 52 0 16 26 3
paars 17 3 30 18 14 6 19 28 1 20 32 2
roze 21 29 5 22 28 2 23 22 1 24 20 4
blauw 25 3 49 26 6 27 27 11 17 28 30 10
oranje 29 35 3 30 43 2 31 42 2 32 57 1
zwart 33 1 74                  
grijs 34 0 67 35 0 72 36 0 62 37 1 50
wit 38 11 12                  
       
Donkergeel (kleur nummer 14) is een kleur die door heel veel mensen in deze steekproef als positief beoordeeld werd. Voor de volgende vraag gaan we ervan uit dat de percentages van de proefpersonen in de tabel ook gelden voor een aselecte steekproef uit de bevolking.
       
4p. 19. Bereken de kans dat in een willekeurige groep van 500 personen 360 personen of meer donkergeel als positief beoordelen.
     

  
Er zijn nu verschillende mogelijkheden om een indeling te maken in positieve, neutrale en negatieve kleuren. In de volgende tabel zie je twee indelingen die de onderzoekers gebruikten. P is het percentage proefpersonen dat een kleur positief beoordeelde en N het percentage dat een kleur negatief beoordeelde.
       
  positieve kleur negatieve kleur
indeling 1 P ≥ 20  en  N ≤ 5 N ≥ 20 en P ≤ 5
indeling 2 P ≥ 30 en N ≤ 10 N ≥ 30 en P ≤ 10
       
Bij indeling 1 is een kleur dus een positieve kleur als ten minste 20% van de proefpersonen de kleur positief beoordeelde en maximaal 5% de kleur negatief noemde. Een voorbeeld daarvan is kleur nummer 29.

Bij indeling 1 zijn er 15 kleuren die positief genoemd worden, terwijl er bij indeling 2 maar 11 positieve kleuren zijn. Toch zijn er kleuren die bij indeling 2 wél en bij indeling 1 niet positief genoemd worden.
       
4p. 20. Onderzoek welke twee kleuren volgens indeling 2 wel tot de positieve kleuren behoren maar volgens indeling 1 niet.
     

  
In de tabel hieronder zie je de resultaten van het tweede deel van het onderzoek waaraan 41 gezonde en 87 depressieve proefpersonen deelnamen. Elke proefpersoon werd gevraagd aan te geven welke kleur het meest overeenstemde met zijn huidige toestand. Deze tabel laat zien hoeveel proefpersonen uit elke groep kozen voor een positieve, neutrale of negatieve kleur.
       
kleur gezond depressief totaal
positief 11 2 13
neutraal 26 31 57
negatief 4 54 58
totaal 41 87 128
       
Op basis van deze gegevens kan de kans bepaald worden dat een proefpersoon die een negatieve kleur koos, daadwerkelijk depressief is.
       
3p. 21. Bereken deze kans.
     

  
Uit het onderzoek van bovenstaande tabel kwam naar voren dat 62,1% van de depressieve proefpersonen een negatieve kleur uitkoos. Van de gezonde proefpersonen koos 9,8% een negatieve kleur uit.

Onderstaande tabel  is een soortgelijke tabel als de vorige tabel, maar nu niet voor de proefpersonen uit het onderzoek, maar voor 1000 willekeurige personen uit de bevolking. In deze situatie komt depressiviteit bij gemiddeld 60 van de 1000 personen voor.
       
kleur gezond depressief totaal
positief      
neutraal      
negatief      
totaal   60 1000
       
Veronderstel dat de genoemde percentages van 62,1% en 9,8% ook in het algemeen gelden. Dan kunnen we met behulp van deze laatste tabel de kans berekenen dat een willekeurige deelnemer aan zo’n bevolkingsonderzoek die een negatieve kleur kiest, inderdaad depressief is.
       
4p. 22. Bereken deze kans.
     

   
UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. Uit de figuur kun je aflezen dat er in 2004 ongeveer 65% grutto's waren (van het aantal in 1990) en in  1994 ongeveer 95% (van het aantal in 1990).
Als 60000 grutto's  65% is, dan is 100% gelijk aan   60000/65 • 100 = 92308 grutto's in 1990
In 1994 zijn er daar dan 95% van, dus  0,95 • 92308 = 87693 grutto's  (afgerond).
   
2. Er is een afname van 100 naar 5 in 15 jaar.
De groeiformule geeft dan 5 = 100 • g15
Je kunt g nu via intersect van je GR berekenen, maar het kan ook algebraïsch:
0,05 = g15
g = 0,051/15 ≈ 0,8190
   
3. aantal van A =  B • 1,042t
aantal van B =  B • 1,016t
Als A tweemaal zo groot is als B, dan moet gelden:   2 • B • 1,1016t  = B • 1,042t
B valt weg:   2 • 1,1016t  = 1,042t
Y1 = 2 * 1,016^X
Y2 = 1,042^X
Intersect geeft  X = t = 27,43 jaar, dus dat is voor het eerst na 28 jaar.

(opm:  in plaats van intersect kun je nu ook handig TABLE van je GR gebruiken)
   
4. De halveringstijd t vind je via  gt = 0,5  ofwel  t =  log(0,5)/log(g)

g = 0,975 geeft  halveringstijd  27,38 jaar
g = 0,965 geeft halveringstijd  19,46 jaar
g = 0,955  (bij aankomst op dag 140)  geeft halveringstijd  15,05 jaar

De verschillen zijn 7,92 jaar (27,38 - 19,46)  en 4,41 jaar (19,46 - 15,05)
dus de halveringstijden nemen NIET met een vast aantal af.
   
5. minder dan 2 cm afwijkend is tussen 278 en 282
normalcdf(287, 282, 280, 0.65) = 0,9979
meer dan 2 cm afwijkend is dan 1 - 0,9979 = 0,0021  en dat is  0,21%
   
6. er moet gelden:   normalcdf(284, 1099, μ, 0.65) = 0,05
Y1 = normalcdf(284, 10^99, X, 0.65)
Y2 = 0,05
intersect geeft  X = 282,93   ≈  283 cm
   
7. Als het gemiddelde van de steekproef groter is dan de streefwaarde, dan is Crechts het kleinst.
Als het gemiddelde dan verder van de streefwaarde af gaat, dan wordt  (rechtergrens - g)  nog kleiner,  dus Crechts ook (de noemer blijft immers gelijk) dus wordt Crechts kleiner, dus C ook.

Precies zo'n verhaal geldt aan de andere kant ook als Clinks de kleinste is.

Dus wordt C altijd kleiner.
   
8. Bij één willekeurige lamp is de kans tussen 0,5º en 2º  gelijk aan  normalcdf(0.5, 2, 1.25, 0,25) = 0,9973
De kans op een lamp NIET tussen de 0,5º en 2º is dan 1 - 0,9973 = 0,0027

Het aantal NIET tussen de 0,5º en 2º is binomiaal verdeeld met n = 50 en p = 0,0027
P(minstens 1) = 1 - P(0) = 1 - binompdf(50, 0.0027, 0) = 0,1264
   
9. Het aantal met hoek groter dan 1,25º is binomiaal verdeeld met n = 50 en p = 0,5
P(X ≥ 34) = 1 - P(X ≤ 33) = 1 - binomcdf(50, 0.50, 33) = 0,0077
   
10. De grafiek van de hst gaat door bijv.  (300, 3)  en  (1000, 5.5)
Dat betekent in  5,5 - 3 = 2,5 uur een afstand van  1000 - 300 = 700 km
De snelheid is dan  700/2,5 = 280 km/uur
   
11. De gewone trein ligt in dat gebied boven de hst, dus de gewone trein gebruikt meer tijd en is dus langzamer.  Uitspraak 1 klopt NIET.

De hst is dus inderdaad sneller dan de gewone trein, dus uitspraak 2 klopt WEL.

De hst grafiek ligt op dit gebied onder beide andere grafieken, dus de hst is sneller dan beide anderen, dus uitspraak 3 klopt WEL.
   
12.
  De grafiek van de auto is een rechte lijn tussen   (0, 0) en  (800, 8).
Zie de paarse lijn hierboven.
Die snijdt de grafiek van het vliegtuig ongeveer bij  400 km
De auto is sneller voor afstanden van 0 - 400 km 
   
13. De reistijden zijn gelijk als   0,00137a + 3,43 = 0,00793a + 1,10
2,33 = 0,00656a
a = 2,33/0,00656 = 355 km
In de grafiek zie je dat voor afstanden vanaf 355 km het vliegtuig een kleinere reistijd heeft.
   
14. log(10A) = log(10) + log(A)  = 1 + log(A)   want log(10) = 10log(10) = 1
Dat is dus één meer dan log(A)
   
15. log(A) = M - 3
A = 10M - 3 = 10M  • 10-3 = 10M  • 0,001
   
16. 2004:  A = 0,001 • 105,3 = 199,53
2011:  102,0 = 100
Dat is  199,53/100 = 1,9953 keer zo groot, dus ongeveer 2 keer zo groot.
   
17. Als de halveringstijd gelijk is aan 8 dagen dan is  g8 = 0,5
g = 0,5(1/8) = 0,917
Eindwaarde is 5,  beginwaarde is  4800 • 5 = 24000
y = B • gt  invullen:   5 = 24000 • 0,917t
Het mag nu met de GR (intersect) maar het kan natuurlijk ook algebraïsch:
5/24000 = 0,0002083 = 0,917t
t = log(0,0002083)/log(0,917) = 97,8 dagen.
   
18. Voor een getal van 0 tm 255 zijn er 256 mogelijkheden.
Voor drie zulke getallen zijn er dan 256 • 256 • 256 = 16777216 mogelijkheden.
   
19. Het aantal personen dat donkergeel positief beoordeelt is binomiaal verdeeld met n = 500 en p = 0,72
P(X ≥ 360) = 1 - P(X ≤ 359) = 1 - binomcdf(500, 0.72, 359) = 0,5228
   
20. Dan moet gelden  (P ≥ 30 en N £ 10)  maar niet dat (P ≥ 20  en  N ≤ 5)
Dat is zo als  5 < N ≤  10  en ook  P  boven de 20
Dat is zo bij kleuren 6 en 28.
   
21. Er waren 58 personen die een negatieve kleur kozen waarvan er 54 daadwerkelijk depressief waren.
De kans is dan 54/58 = 0,9310
   
22. Ga de tabel maar invullen:
 
kleur gezond depressief totaal
positief      
neutraal      
negatief 92 37 129
totaal 940 60 1000
   
  bij 1000 personen zijn 940 gezonden
van die 940 kiezen er 0,098 • 940 = 92 negatief
van de 60 depressieven kiezen er  0,621 • 60 = 37 negatief
in totaal kiezen er dan  92 + 37 = 129 negatief
dat is  37/129 • 100% = 28,7%