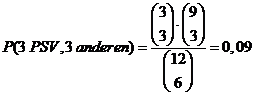Nieuwe pagina 1

VWO WC, 2013 - I

Lichaamsoppervlak.

De buitenkant van je lichaam is je lichaamsoppervlak. Gegevens over iemands lichaamsoppervlak worden bijvoorbeeld gebruikt voor risicoanalyse bij bestrijdingsmiddelen. De schadelijke stoffen hierin kunnen via de huid in het lichaam worden opgenomen. In een rapport van het RIVM (Rijksinstituut voor Volksgezondheid en Milieu) is een tabel te vinden waarin onder andere de lichaamsoppervlakte is af te lezen. Een gedeelte van deze tabel is hieronder weergegeven.

	lichaamsoppervlakte in % van de totale oppervlakte
leeftijd	hoofd	romp	armen en handen	benen en voeten
1,5 jaar	16,2	34,0	18,15	31,65
17,5 jaar	8,1	32,1	21,0	38,8

Bij jonge kinderen is het hoofd ten opzichte van de rest van het lichaam relatief groot. Als kinderen ouder worden, groeien de armen en handen en de benen en voeten sneller dan de rest van het lichaam.

Het aandeel van armen en handen in de lichaamsoppervlakte is voor kinderen in de periode van 1,5 jaar tot 17,5 jaar gestegen van 18,15% naar 21,0%. Ook het aandeel van de benen en voeten is in die 16 jaar groter geworden.

3p.

Onderzoek of de relatieve toename van het aandeel van armen en handen groter is dan de relatieve toename van het aandeel van benen en voeten.

In het RIVM-rapport vinden we ook gegevens over de lichaamsgewichten van kinderen. Als kinderen ouder worden, neemt het gemiddelde lichaamsgewicht toe. Ook de standaardafwijking van het lichaamsgewicht neemt toe. Het gemiddelde lichaamsgewicht van kinderen van 12,5 jaar is 44,8 kg. De 25% lichtste kinderen van 12,5 jaar hebben een lichaamsgewicht van hoogstens 39,3 kg.

In de rest van deze opgave nemen we aan dat voor iedere leeftijdsgroep het lichaamsgewicht normaal verdeeld is.

4p.

Bereken de standaardafwijking van het lichaamsgewicht op 12,5-jarige leeftijd in één decimaal nauwkeurig.

In het rapport zijn de gegevens over de lichaamsgewichten van jongens en meisjes ook apart vermeld. Bij 4,5-jarigen hebben de jongens een gemiddeld lichaamsgewicht van 18,7 kg en een standaardafwijking van 3,0 kg. Voor de meisjes geldt een gemiddeld lichaamsgewicht van 18,0 kg en een standaardafwijking van 3,3 kg.
We bekijken het minimale lichaamsgewicht van de 10% zwaarste meisjes van 4,5 jaar oud.

3p.

Toon aan dat het minimale lichaamsgewicht van de 10% zwaarste meisjes van 4,5 jaar oud ongeveer 22,2 kg is. Geef je antwoord in twee decimalen nauwkeurig.

Een bepaald percentage van de jongens van 4,5 jaar oud weegt meer dan 22,2 kg.

3p.

Bereken dit percentage.

Er zijn ook formules waarmee we de lichaamsoppervlakte kunnen berekenen.

Voor het berekenen van de lichaamsoppervlakte bij kinderen worden vooral de volgende twee formules gebruikt:

In deze formules is S de lichaamsoppervlakte in m², L de lichaamslengte in cm en M het lichaamsgewicht in kg.

Voor een kind met een lengte van 1 meter (L = 100) blijken de grafieken van de formules van Mosteller en Haycock bijna samen te vallen. Behalve bij M = 0 kg is er bij L = 100 nóg een lichaamsgewicht waarbij de formule van Mosteller en de formule van Haycock precies dezelfde lichaamsoppervlakte geven.

4p.

Bereken dat lichaamsgewicht in één decimaal nauwkeurig.

Om de formules nog beter met elkaar te kunnen vergelijken, is het handig om de formule van Mosteller in dezelfde vorm te schrijven als de formule van Haycock.

De formule van Mosteller kan geschreven worden in de vorm S_Mosteller = c • L^0,5 • M^0,5

3p.

Laat dat zien en bereken de waarde van c.

Dialecten vergelijken.

Taalkundigen doen veel onderzoek naar de dialecten in Nederland en Vlaanderen. Onderzoeker M. Spruit onderzocht in 2008 in hoeverre dialecten op elkaar lijken. De mate waarin twee dialecten verschillen, wilde hij uitdrukken in een getal. Daarom vergeleek hij steeds twee dialecten op een aantal kenmerken en telde hij vervolgens de verschillen. Elk verschil tussen deze twee dialecten leverde een punt op. Het totale aantal punten is de Hammingafstand tussen deze twee dialecten.
Bijvoorbeeld: in Lunteren kan men zeggen: “Jan herinnert zich dat verhaal wel”, maar ook: “Jan herinnert z’n eigen dat verhaal wel”. In Veldhoven zegt men altijd: “Jan herinnert zich dat verhaal wel”. In geen van beide dialecten gebruikt men hier “hem” of “zichzelf” of “hemzelf”, iets dat in andere dialecten wel voorkomt.

Het vergelijken van deze vijf kenmerken levert dus in totaal 1 punt op voor de Hammingafstand. Dat is in de volgende tabel weergegeven.

	Lunteren	Veldhoven	punten (voor Hammingafstand)
zich	+	+	0
hem	-	-	0
z'n eigen	+	-	1
zichzelf	-	-	0
hemzelf	-	-	0

Stel men vergelijkt dialect X met het dialect van Lunteren. En stel dat vergelijken van de vijf kenmerken uit de tabel in totaal 3 punten oplevert voor de Hammingafstand. In dialect X wordt ook “zich” gebruikt.

4p.

Schrijf alle mogelijkheden voor deze vijf kenmerken voor dialect X op. Gebruik hiervoor de volgende tabel.

	Lunteren	Dialect X
zich	+
hem	-
z'n eigen	+
zichzelf	-
hemzelf	-

De onderzoeker vergeleek niet vijf, maar 507 kenmerken. Het resultaat is een tabel waarin per tweetal dialecten de Hammingafstand te zien is. In onderstaande tabel zie je hier een gedeelte van.
Het getal 66 in deze tabel voor het tweetal Lunteren-Bellingwolde (of Bellingwolde-Lunteren) betekent dat bij deze twee dialecten 66 van de 507 kenmerken verschillen: de Hammingafstand is 66.

Dialect	Lunteren	Bellingwolde	Hollum	Doel	Sint-Truiden	Veldhoven
Lunteren	-	66	52	122	77	47
Bellingwolde	66	-	56	134	81	51
Hollum	52	56	-	116	63	59
Doel	122	134	116	-	115	111
Sint-Truiden	77	81	63	115	-	72
Veldhoven	47	51	59	111	72	-

In deze tabel heeft de onderzoeker dus 15 Hammingafstanden berekend.
In totaal stonden er echter geen 6 dialecten, maar 267 dialecten in de tabel. Bij elk tweetal heeft de onderzoeker de Hammingafstand berekend.

3p.

Bereken hoeveel Hammingafstanden de onderzoeker in totaal heeft berekend.

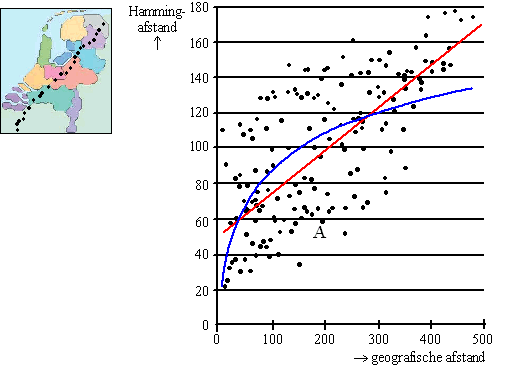
De onderzoeker zocht naar een verband tussen de geografische afstand en de Hammingafstand van dialecten. In het kaartje in de figuur zie je een aantal dialecten met stippen aangegeven. In het assenstelsel is voor elk tweetal dialecten de Hammingafstand (in punten) uitgezet tegen de geografische afstand (in km).
In het assenstelsel kun je zien dat bij punt A de afstand tussen twee plaatsen gelijk is aan 200 km en de Hammingafstand ongeveer gelijk is aan 58.

De onderzoeker heeft op twee manieren geprobeerd het verband tussen de geografische afstand en de Hammingafstand met een wiskundig verband te benaderen. Beide manieren, een lineair verband en een logaritmisch verband, zijn weergegeven in het assenstelsel.

4p.

Stel een formule op voor het lineaire verband in de figuur.

De onderzoeker heeft in het assenstelsel dus ook een grafiek voor een logaritmisch verband getekend. De formule voor dit logaritmische verband is: H = - 45,88 + 66,44log(x)
Hierin is H de Hammingafstand en x de geografische afstand in km.

Als de geografische afstand verdubbelt, neemt de Hammingafstand steeds met dezelfde waarde toe.

5p.

10.

Bereken deze waarde.

Voetbalplaatjes.

In het voetbalseizoen 2008-2009 hield een grote supermarktketen een actie: bij elke besteding van 10 euro aan boodschappen kreeg je één zakje met vijf voetbalplaatjes. Deze plaatjes konden in een verzamelalbum geplakt worden waarin de 18 eredivisieclubs stonden. Per club kon je 15 plaatjes inplakken. In totaal waren er dus 18•15 = 270 verschillende plaatjes. Er zijn miljoenen plaatjes gedrukt. We nemen aan dat de plaatjes willekeurig over de zakjes verdeeld werden en dat er van alle plaatjes evenveel waren.

Het is mogelijk dat er vijf plaatjes van dezelfde club in een zakje zitten (daar kunnen dan nog dubbele plaatjes bij zitten).
De kans op vijf plaatjes van dezelfde club is heel klein.

4p.

11.

Bereken deze kans. Rond je antwoord af op zeven decimalen.

Karin, die niet van voetballen houdt, heeft 12 plaatjes waaronder 3 van PSV. Peter en Maarten krijgen ze. Peter mag blindelings 6 plaatjes trekken uit de 12; de 6 die overblijven zijn voor Maarten.

4p.

12.

Bereken de kans dat Peter alle drie de plaatjes van PSV trekt.

In het verzamelalbum stond ook een spelletje dat je kunt spelen om aan meer plaatjes te komen. Het gaat als volgt:
Op ieder spelersplaatje staan twee cijfers. Het bovenste cijfer is een soort ‘rapportcijfer’ voor de aanvallende kwaliteiten van de speler, het onderste voor zijn verdedigende kwaliteiten. De speler in onderstaande figuur heeft voor aanvallende kwaliteiten het cijfer 3 en voor verdedigende kwaliteiten een 6.

Bij dit spelletje kiest iedere deelnemer een voetbalplaatje uit zijn eigen verzameling en legt dit omgedraaid op tafel, zodat de cijfers niet te zien zijn. De deelnemers spreken af of ze spelen om aanvallende of verdedigende kwaliteiten. Dan draaien ze de plaatjes om. De deelnemer met het hoogste cijfer op de gekozen kwaliteit krijgt beide plaatjes.

Yvonne en Kees spreken af dat ze spelen om aanvallende kwaliteiten. Yvonne heeft twee plaatjes met de cijfers 8 en 5 op deze kwaliteit en Kees heeft twee plaatjes met de cijfers 7 en 3 op deze kwaliteit. Ze leggen ieder eerst één plaatje op tafel en bepalen wie gewonnen heeft. Daarna doen ze hetzelfde met hun tweede plaatje.

4p.

13.

Geef alle mogelijke spelverlopen en bereken daarmee hoeveel plaatjes Yvonne naar verwachting na dit spel zal hebben.

De Rijksuniversiteit Groningen heeft een programma ontwikkeld om met behulp van ‘rapportcijfers’ voor de kwaliteiten van spelers een optimaal team samen te stellen: de Computer Coach. Dit programma is onder andere gebruikt voor FC Groningen.
Alle spelers krijgen voor 50 verschillende kwaliteiten een rapportcijfer. De ‘Computer Coach’ berekent dan met behulp van vooraf geformuleerde eisen het optimale team.

Met behulp van de voetbalplaatjes kunnen we in een sterk vereenvoudigde situatie zien hoe de ‘Computer Coach’ te werk gaat. Op ieder spelersplaatje staan twee cijfers. Het bovenste cijfer is een soort ‘rapportcijfer’ voor de aanvallende kwaliteiten van de speler, het onderste voor zijn verdedigende kwaliteiten. In figuur 2 heeft speler A bijvoorbeeld voor aanvallende kwaliteiten het cijfer 5 en voor verdedigende kwaliteiten een 8.
We gaan uit van een minivoetbalteam: één keeper K en vier andere spelers A, B, C en D. De keeper heeft een vaste plaats en daarom laten we hem verder buiten beschouwing. Van de andere vier spelers worden er twee opgesteld in de aanval en twee in de verdediging. In de volgende figuur zie je hiervan een voorbeeld.

aanval
verdediging

Men kan de totale waarde van de opstelling van deze figuur nu als volgt berekenen: de cijfers voor de aanvallende kwaliteiten van A en B plus de cijfers van de verdedigende kwaliteiten van C en D, dus 5 + 4 + 8 + 6 = 23.
Het gaat er in deze vereenvoudigde situatie alleen om wie er in de aanval en wie in de verdediging staan en niet wie er links en wie er rechts staat.
Er zijn nog meer opstellingen mogelijk. Hoe hoger de totale waarde van een opstelling, des te beter de opstelling.

4p.

14.

Onderzoek wat de beste opstelling is. Licht je antwoord toe.

DNA-bewijs.

Ieder mens heeft DNA in al zijn cellen. Van een persoon, bijvoorbeeld een verdachte van een misdrijf, kan men een zogenoemd DNA-persoonsprofiel maken. Het Nederlands Forensisch Instituut (NFI) verzamelt alle DNA-persoonsprofielen in een DNA-databank. In de figuur zie je de groei van het aantal DNA-persoonsprofielen in de DNA-databank in de periode 2001 tot 2007.



Het aantal DNA-persoonsprofielen is in de periode 2001-2005 bij benadering exponentieel gegroeid van 1000 op 1 januari 2001 tot 7500 op 1 april 2005.

5p.	15.	Toon met behulp van deze gegevens aan dat het aantal DNA-persoonsprofielen in deze periode met ongeveer 4,03% per maand groeide.

In februari 2005 is wettelijk vastgelegd dat van bepaalde groepen veroordeelden DNA-persoonsprofielen worden gemaakt. In de figuur is duidelijk te zien dat vanaf 1 mei 2005 het aantal DNA-persoonsprofielen in de databank sneller is gaan groeien. Het aantal DNA-persoonsprofielen is vanaf 1 januari 2007 tot 1 juli 2007 bij benadering lineair gegroeid. Neem aan dat deze groei zich in de jaren daarna zo voortzet.

4p.	16.	Bereken hoeveel DNA-persoonsprofielen er dan op 1 september 2013 in de databank zouden zitten. Je mag hierbij gebruikmaken van de figuur. Rond je antwoord af op duizendtallen.

Van sporen bij een misdrijf, bijvoorbeeld haren of bloedvlekken, wordt vaak een DNA-spoorprofiel gemaakt. In september 2009 zaten er in werkelijkheid ongeveer 88000 DNA-persoonsprofielen en 40000 DNA-spoorprofielen in de databank. Door een DNA-spoorprofiel te vergelijken met een DNA-persoonsprofiel, kan men achterhalen van wie het spoor geweest zou kunnen zijn. Als twee DNA-profielen in de databank overeenkomen, spreekt men van een match. Het kan hier gaan om het profiel van een spoor en een persoon maar ook om het profiel van twee sporen. DNA-profielen worden gebruikt als bewijsmateriaal bij een misdrijf. Vaak kan er slechts gebruik gemaakt worden van een onvolledig DNA-spoorprofiel dat bij een misdrijf wordt aangetroffen. De kans dat het DNA-persoonsprofiel van een onschuldige toevallig past bij dit onvolledige profiel, hangt af van veel factoren en is niet bij elk profiel gelijk. Een voordeel van een grote DNA-databank is dat men soms oude misdrijven kan oplossen door naar matches te zoeken. Bij een grote databank is de kans groter dat er een match gevonden wordt. Het volgende voorbeeld laat dit zien. Stel men heeft van een misdrijf een onvolledig DNA-spoorprofiel. De kans dat dit onvolledige DNA-spoorprofiel past bij het DNA-persoonsprofiel van een onschuldige is 0,00005. In de databank zitten de DNA-profielen van 88000 personen. Neem aan dat de personen in de databank niet schuldig zijn aan dit misdrijf.

4p.	17.	Bereken de kans dat het DNA-persoonsprofiel van precies één persoon uit de databank past bij het DNA-spoorprofiel.

In het volgende voorbeeld zien we dat je personen vrijwel nooit kunt veroordelen alleen op grond van DNA-profielen. In een museum wordt op een vermoord slachtoffer een spoor gevonden van de dader. Hiervan wordt een onvolledig DNA-spoorprofiel gemaakt. De kans dat dit profiel past bij het DNA-persoonsprofiel van een onschuldige is 0,001. Ten tijde van de moord waren er 800 mensen in het museum, die allemaal het spoor achtergelaten zouden kunnen hebben. Van 100 hiervan is het DNA-persoonsprofiel opgesteld en het blijkt dat bij één persoon het persoonsprofiel past bij het gevonden spoorprofiel. Zelfs als deze persoon in werkelijkheid de dader is, kan men hem op grond van alleen dit DNA-bewijs niet veroordelen. Er is namelijk een redelijk grote kans dat er bij de niet-geteste personen nog één of meer personen zijn waarvan het DNA-persoonsprofiel past bij het DNA-spoorprofiel.

4p.	18.	Bereken deze kans.

Overlevingscurven.

In Vlaanderen is onderzoek gedaan naar het aantal sterfgevallen voor verschillende leeftijden. In onderstaande figuur zie je het aantal sterfgevallen per 10000 mannen in Vlaanderen in het jaar 1971 en in het jaar 1999.



Volgens de grafiek in deze figuur haalden in 1999 van 10000 mannen van 82 jaar 1000 mannen niet hun 83^e verjaardag. Neem daarom aan dat voor elke 82-jarige man ook tegenwoordig nog een kans van 10% bestaat om binnen een jaar te overlijden.

4p.	19.	Bereken hoe groot de kans dan is dat van 100 willekeurig gekozen 82-jarige mannen er meer dan 95 na een jaar nog in leven zijn.

De verticale schaalverdeling in de figuur is logaritmisch. Voor mannen ouder dan 35 jaar verloopt de grafiek in de figuur die hoort bij 1999 ongeveer volgens een rechte lijn door de punten (35, 10) en (80, 1000). Voor dit gedeelte geldt daarom het volgende exponentiële verband: M_t = b • g^t Hierin is M_t het aantal mannen met een leeftijd van t jaar die in 1999 overleden per 10000 mannen van t jaar.

4p.	20.	Bepaal de waarde van b en g in deze formule. Rond je antwoorden af op drie decimalen.

Met behulp van de gegevens van bovenstaande figuur kunnen zogenoemde overlevingscurven gemaakt worden. Die overlevingscurven zijn theoretische modellen: het zijn grafieken waarin je kunt aflezen hoeveel overlevenden er nog over zijn op een bepaalde leeftijd als je begint met een denkbeeldige groep van 100000 mensen. In de volgende figuur zie je in één grafiek de twee overlevingscurven zoals die gelden voor 100000 mannelijke inwoners van Vlaanderen als voor deze mannen op elke leeftijd de sterftekansen van 1971 of die van 1999 zouden gelden.



Zo lees je in deze figuur af dat er van de denkbeeldige groep van 100000 mannen nog 79000 mannen over zijn op 60-jarige leeftijd als we uitgaan van de sterftekansen van 1971. Om met behulp van deze curven conclusies te trekken over de sterfte in Vlaanderen doen we alsof het hier wel twee werkelijke groepen van 100000 mannen betreft. We kijken naar de leeftijd waarop 50% van zo’n groep van 100 000 mannen nog in leven is. Aan de hand hiervan karakteriseerde een bevolkingsonderzoeker de ontwikkeling van de sterfte tussen 1971 en 1999 met de volgende slogan: “Elk jaar bijna een seizoen ouder”. Een seizoen betekent in dit verband een periode van 3 maanden.

4p.	21.	Onderzoek met behulp van de figuur de juistheid van deze slogan.


bronvermelding figuur na opgave 13 voetbalplaatje AH figuur na opgave 12 voetbalplaatjes AH

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

armen en handen zijn gestegen van 18,15 naar 21,0.
Dat is een stijging van 2,85 en dat is ^2,85/_18,15 • 100% = 15,7%

benen en voeten zijn gestegen van 31,65 naar 38,8
Dat is een stijging van 7,15 en dat is ^7,15/_31,65 • 100% = 22,6%

Dus benen en voeten zijn relatief het meest toegenomen.

normalcdf(0, 39.3, 44.8, X) = 0,25
Y1 = normalcdf(0, 39.3, 44.8, X) en Y2 = 0,25 en dan intersect levert X = σ = 8,15 kg

normalcdf(X, 1000000..., 18, 3.3) = 0,10
Y1 = Normalcdf(X, 100000..., 18, 3.3) en Y2 = 0,10 en dan intersect geeft X = 22,23 kg.

normalcdf(22.2, 1000..., 18.7, 3.0) = 0,1216

er moet gelden √(¹/₃₆₀₀ • 100 • M) = 0,024265 • 100^0,3964• M^0,5378Y1 = √(¹/₃₆₀₀ * 100 * X) en Y2 = 0,024265 * 100^0,3964* X^0,5378 en dan intersect geft X= 14,6 kg.

gewoon uitschrijven:
(de rij met "zich" moet allemaal + geven)
in elke kolom moeten 3 verschillen met Lunteren zitten.

	Lunteren	Dialect X
zich	+	+	+	+	+
hem	-	-	+	+	+
z'n eigen	+	-	+	-	-
zichzelf	-	+	+	-	+
hemzelf	-	+	+	+	-

Hoeveel tweetallen kun je maken van 267 dialecten?
Dat zijn er 267 nCr 2 = 35511

Een rechte lijn door bijv. (10, 55) en (400, 145) (aflezen uit de figuur).
^Δ^y/_Δ_x = ^{(145 - 55)}/_{(400 - 10)} = 0,2308
H = 0,2308 • x + b
Vul een punt in, bijv. (10, 55)
Dat geeft 55 = 0,2308 • 10 + b ⇒ b = 52,7
De vergelijking is dan H = 0,2308x + 52,7

10.

-45,88 + 66,44log(2x)
= -45,88 + 66,44 • (log2 + logx)
= -45,88 + 66,44 • log2 + 66,44 • logx
= -45,88 + 20 + 66,44 • logx

11.

Het eerste plaatje doet er niet toe, de volgende vier moeten per se van dezelfde club als het eerste zijn.
De kans daarop is per plaatje ¹/₁₈.
In totaal is de kans dus (¹/₁₈)⁴ = 0,0000095

12.

13.

de mogelijke spelverlopen zijn:
8-7-5-3 en Yvonne wint er 2
5-3-8-7 en Yvonne wint er 2
8-3-5-7 en Yvonne wint er één en verliest er één
5-7-8-3 en Yvonne wint er één en verliest er één

P(2 winst) = 0,5 en dat geeft +2 plaatjes
P(1 winst, 1 verlies) = 0,5 en dat geeft + 0 plaatjes

De verwachtingswaarde is dan 0,2 • 2 + 0,5 • 0 = +1
Na afloop heeft ze dan naar verwachting 3 plaatjes

14.

Dit zijn alle mogelijkheden:

aanval	verdediging	waarde
A + B A + C A + D B + C B + D C + D	C + D B + D B + C A + D A + C A + B	5 + 4 + 8 + 6 = 23 5 + 7 + 7 + 6 = 25 5 + 4 + 7 + 8 = 24 4 + 7 + 8 + 6 = 25 4 + 4 + 8 + 8 = 24 7 + 4 + 8 + 7 = 26

De beste opstelling is C en D in de aanval en A en B in de verdediging.

15.

van 1 januari 2001 tot 1 april 2005 is 51 maanden
In die 51 maanden is de factor ⁷⁵⁰⁰/₁₀₀₀ = 7,5
Dus g⁵¹ = 1,5 ⇒ g = 7,5^1/51 = 1,0403
Dat is 4,03% groei per maand.

16.

op 1 juli 2007 zijn er ongeveer 38000 DNA-persoonsprofielen
op 1 januari 2007 zijn er ongeveer 27500 DNA-persoonsprofielen
dat is een toename van ^{(38000 - 28000)}/₆ = 1667 profielen per maand.
van 1 juli 2007 tot 1 september 2013 is 74 maanden
dan komt er nog 74 • 1667 ≈ 123000 profielen bij
dan zijn er 38000 + 123000 = 161000 profielen

17.

dit is een binomiale verdeling met n = 88000 en p = 0,00005
P(X = 1) = binompdf(88000, 0.00005, 1) = 0,0540

18.

er zijn nog 700 andere personen.
Dit is een binomiale verdeling met n = 700 en p = 0,001
P(X ≥ 1) = 1 - P(X ≤ 0) =1 - binomcdf(700, 0.001, 0) = 0,5036

19.

het aantal sterfgevallen is binomiaal verdeeld met n = 100 en p = 0,10
P(X ≤ 4) = binomcdf(100, 0.10, 4) = 0,0237

20.

de factor is ¹⁰⁰⁰/₁₀ = 100 en dat is in 80 - 35 = 45 jaar.
dus g⁴⁵ = 100 ⇒ g = 100^1/45 = 1,10775....
vul nu bijv. t = 35 en M = 10 in: 10 = B • 1,10775....³⁵ ⇒ 10 = B • 35,93... ⇒ B = 0,278
Dat geeft de formule M = 0,278 • 1,108^t

21.

lees af bij y = 50000 (50% nog in leven)
voor de groep van 1971 geeft dat ongeveer 72 jaar
voor de groep van 1999 geeft dat ongeveer 78 jaar
in 28 jaar (van 1971 tot 1999) is dat een stijging van 6 jaar
Per jaar is dat ⁶/₂₈ = 0,21 jaar en dat is 0,21 • 12 = 2,6 maanden, dus dat is inderdaad bijna een seizoen.