Nieuwe pagina 1

VWO WC, 2010 - I

Verzekering.

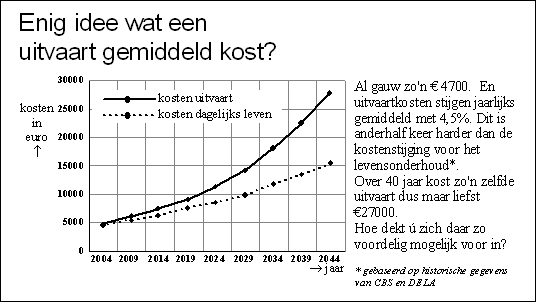
Verzekeringsmaatschappijen maken op verschillende manieren reclame voor allerlei verzekeringen. Een voorbeeld daarvan vind je in de figuur hieronder. Daar zie je een deel van een reclamefolder die in 2004 huis aan huis werd verspreid. In de folder legt de verzekeraar uit dat de kosten voor een uitvaart sneller stijgen dan de kosten voor het levensonderhoud. Ook wordt de ontwikkeling van beide kostensoorten met een grafiek in beeld gebracht.



Uitgaande van een jaarlijkse kostenstijging met 4,5% berekende men de kosten in 2044. De uitvaartkosten stijgen van € 4700 in 2004 tot ongeveer € 27 000 in 2044. Het bedrag in 2044 is afgerond op duizendtallen.

3p.	1.	Bereken dit bedrag in euro’s nauwkeurig.

Met “anderhalf keer harder” bedoelt de schrijver van de folder dat de jaarlijkse procentuele stijging van de kosten voor een uitvaart 1,5 keer zo groot is als die van de kosten voor het levensonderhoud. Daardoor zullen de kosten voor het levensonderhoud in de periode 2004─2044 stijgen met een percentage dat aanzienlijk kleiner is dan 474% (het stijgingspercentage van de uitvaartkosten). Dit is in de folder ook grafisch weergegeven.

3p.	2.	Bereken met hoeveel procent de kosten voor het levensonderhoud volgens de folder zullen toenemen in de periode 2004─2044.

Boomgroei.

Naar de groei van bomen is veel onderzoek gedaan. Dat heeft geleid tot een goed inzicht in het verband tussen de hoogte van een boom en de leeftijd van die boom. In de bosbouw wordt voor veel bomen de te verwachten hoogte berekend met de formule van Chapman-Richards:

h = a(1 - b^t)^c

Hierin is h de hoogte van een boom in meters en t de leeftijd in jaren. De waarden van de getallen a, b en c hangen af van de soort boom. De getallen a, b en c zijn positief. In de volgende tabel zijn deze waarden voor enkele boomsoorten weergegeven.

boom	a	b	c
Japanse lariks	23,743	0,9603	1,22770
zomereik	39,143	0,9867	0,96667
Amerikaanse eik	29,026	0,9790	0,80820
berk	43,281	0,9876	0,95040
grove den	24,426	0,9656	1,59980

Het verband tussen de hoogte en de leeftijd van de zomereik wordt dus gegeven door de formule:

h = 39,143(1 - 0,9867^t)^0,96667

De zomereik wordt op den duur veel groter dan de Amerikaanse eik, maar in de eerste levensjaren groeit de Amerikaanse eik veel sneller.

5p.

Toon door berekening aan dat volgens de formule van Chapman-Richards de Amerikaanse eik in het vierde levensjaar ruim 20 cm méér groeit dan de zomereik.

Pas na een groot aantal jaren is de zomereik groter dan de Amerikaanse eik.

3p.

Bereken na hoeveel jaren dit volgens de formule van Chapman-Richards voor het eerst het geval is.

Voor de formule voor de zomereik hebben we gebruik gemaakt van de waarden van a, b en c uit de tabel. Maar niet alle zomereiken hebben de waarde 39,143 voor a.
Factoren zoals klimaat en bodemgesteldheid beïnvloeden de waarde van a.
Chapman en Richards gaan er in hun model van uit dat de waarden van b en c uitsluitend afhangen van de boomsoort.
Vaak weet men niet van tevoren welke waarde van a een boom heeft. Om de waarde van a voor een boom te bepalen, laat men de boom eerst een aantal jaren groeien.
Daarna meet men de boom op en berekent men welke waarde van a past bij de groei van die boom. Men gaat ervan uit dat die waarde van a daarna niet meer verandert.

Een zomereik bereikt op de leeftijd van 10 jaar een hoogte van 6,18 meter.

3p.

Bereken de waarde van a die hierbij hoort.

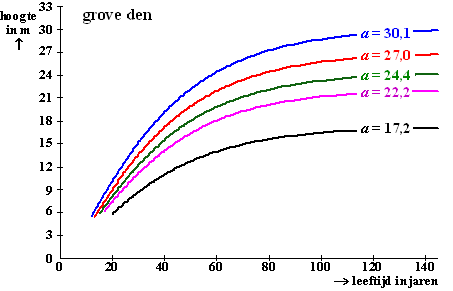
Afhankelijk van de waarde van a krijgen we verschillende groeiformules. In de volgende figuur zie je de grafieken van enkele groeiformules van de grove den. De waarde van a staat er steeds bij vermeld.

Als je naar deze figuur kijkt, kun je je afvragen of deze grafieken door de oorsprong (0, 0) gaan als we ze verder naar links zouden doortekenen. Dit is inderdaad het geval.
Sterker nog: dit is het geval voor alle grafieken die horen bij de algemene formule h(t) = a(1 − b^t)^c van Chapman-Richards.

4p.

Beredeneer, dus zonder getallenvoorbeelden te gebruiken, dat alle grafieken die horen bij de formule van Chapman-Richards door de oorsprong gaan.

Stoppen met roken.

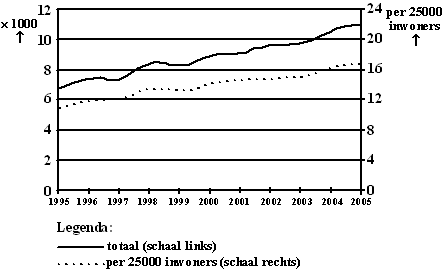
Veel mensen beginnen op jonge leeftijd met roken en proberen daar op latere leeftijd weer mee op te houden. Dat lukt niet altijd.
Het Centraal Bureau voor de Statistiek (CBS) publiceert regelmatig cijfers waarmee het rookgedrag van Nederlanders kan worden bestudeerd. In de volgende tabel vind je enkele getallen.

rokers en aantallen sigaretten
jaar	2001	2005
aantal Nederlanders, in miljoenen	16,0	16,3
percentage rokers	33,3%	29,5%
gemiddeld aantal sigaretten per roker per jaar	4526	4271

4p.

Bereken met hoeveel procent het totale aantal gerookte sigaretten in 2005 is afgenomen ten opzichte van 2001.

Er zijn veel hulpmiddelen om minder te gaan roken of er zelfs helemaal mee te stoppen. Eén daarvan is het gebruik van tabletten van het merk Fumostop.
Om na te gaan of Fumostop een middel is dat inderdaad helpt, wordt het volgende onderzoek uitgevoerd.
Uit alle zware rokers wordt aselect een groep van 18 proefpersonen gekozen. Elke proefpersoon krijgt 10 tabletten die uiterlijk niet van elkaar verschillen. De tabletten zijn verpakt in doordrukstrips met bij elk tablet een nummer. Zie de figuur.

Elke proefpersoon moet 10 dagen lang iedere dag bij het opstaan één willekeurig gekozen tablet innemen, het nummer van dat tablet noteren en bijhouden hoeveel sigaretten hij die dag rookt.
Wat de proefpersonen niet weten maar de onderzoekers wel, is dat 5 van de tabletten inderdaad van het merk Fumostop zijn. De andere 5 tabletten bevatten geen enkele werkzame stof. We geven de ‘echte’ tabletten aan met F en de andere tabletten met NF. Aan de genoteerde tabletnummers kunnen de onderzoekers zien wanneer de F- en de NF-tabletten ingenomen zijn.

Nico is één van de 18 proefpersonen. De mogelijkheid bestaat dat hij op dag 1 start met een F-tablet en vervolgens om de andere dag een F-tablet inneemt.
Dus: op dag 1 een F-tablet, op dag 2 een NF-tablet, op dag 3 een F-tablet, enzovoort.

3p.

Bereken deze kans.

Het kan gebeuren dat een proefpersoon de eerste dag van het onderzoek een F-tablet inneemt. De kans dat niemand van de 18 proefpersonen dit doet, is volgens de onderzoekers echter erg klein.

3p.

Bereken deze kans.

De proefpersonen kiezen hun tabletten iedere dag dus volledig aselect. Het kan dus gebeuren dat een proefpersoon de eerste dag een van de tabletten met nummer 1 of nummer 2 kiest.

4p.

10.

Bereken hoe groot de kans is dat 6 of meer proefpersonen op de eerste dag van het onderzoek een van de tabletten met nummer 1 of 2 kiezen.

Van de mensen die in 2006 rookten, rookte 24,5% per dag 20 sigaretten of meer. Rokers rookten toen gemiddeld 11,4 sigaretten per dag. Tine wil onderzoeken of het aantal sigaretten per dag normaal verdeeld zou kunnen zijn.
Ze bedenkt de volgende aanpak: “Als er sprake is van een normale verdeling, dan kan ik de bijbehorende standaardafwijking berekenen. Daarna kan ik nagaan of die waarde – in combinatie met dat gemiddelde 11,4 – tot een conclusie leidt.”

4p.

11.

Bereken die standaardafwijking en toon daarmee aan dat het aantal sigaretten dat een roker per dag in 2006 rookte, niet normaal verdeeld kan zijn.

Schoonheidssalons.

Begin 2005 waren er in Nederland 10820 schoonheidssalons. Daarvan hadden er 9846 geen ander personeel in dienst dan alleen de eigenaar. Bij de overige schoonheidssalons werkten dus 2 of meer personen. Daarover zie je in de volgende tabel enkele gegevens.

aantal personen in dienst	totaal aantal personeelsleden
1	9846
2	1298
3 of 4	757
meer dan 4	1298

3p.

12.

Bereken hoeveel procent van de schoonheidssalons 2 mensen in dienst had.

Tien jaar eerder waren er veel minder schoonheidssalons. In het begin van 1995 telde Nederland er 6800.
We gaan ervan uit dat het aantal schoonheidssalons in de periode 1995–2005 lineair toegenomen is en dat dit in de jaren daarna op dezelfde manier verder gaat.

3p.

13.

Bereken hoeveel schoonheidssalons er dan zullen zijn in het begin van het jaar 2012.

We kunnen ook naar het aantal schoonheidssalons per 25000 inwoners kijken. Zie daarvoor onderstaande figuur.
We geven het aantal schoonheidssalons aan met A en lezen de bijbehorende aantallen (x 1000) af op de linkeras. Het aantal schoonheidssalons per 25000 inwoners geven we aan met V en de daarbij behorende aantallen staan op de
rechteras.
In de figuur is de ontwikkeling van zowel A als V weergegeven voor de periode 1995–2005.

De grafieken deze figuur kunnen zonder veel verlies van informatie door rechte lijnen vervangen worden. De lijnen van A en V lopen ongeveer evenwijdig. Dat kan het gevolg zijn van het gebruik van twee verschillende verticale assen in de figuur.
Het is de vraag of de grafieken nog steeds (ongeveer) evenwijdig zijn wanneer we deze tekenen in een assenstelsel met één verticale as voor beide grafieken.

3p.

14.

Onderzoek of dat inderdaad het geval is. Motiveer je antwoord.

In China zijn tegenwoordig zeer veel schoonheidssalons te vinden. Begin 2005 waren dat er 1,6 miljoen, terwijl het land toen ongeveer 1300 miljoen inwoners telde.
Om Nederland en China goed met elkaar te kunnen vergelijken, kijken we naar het aantal schoonheidssalons per 25000 inwoners.
In bovenstaande figuur hebben we gezien dat in Nederland het aantal schoonheidssalons per 25000 inwoners ongeveer lineair toeneemt. We gaan ervan uit dat deze lineaire groei na 2005 op dezelfde wijze doorgaat. Het aantal schoonheidssalons in Nederland per 25000 inwoners geven we nu aan met VN. Dan geldt bij benadering:

V_N = 17 + 0,6t

In deze formule is t de tijd in jaren met t = 0 voor het begin van 2005. Met V_C geven we het aantal schoonheidssalons in China per 25 000 inwoners aan. Dat aantal blijkt in China niet lineair, maar bij benadering exponentieel toe te nemen. Iemand heeft vastgesteld dat de volgende formule voor V_C dit proces goed beschrijft:

V_C = 30,8 • 1,06^t

Hierbij is t de tijd in jaren met t = 0 voor het begin van 2005. Volgens de bovenstaande formules zullen beide landen nog deze eeuw 1 schoonheidssalon op de 500 inwoners hebben.

4p.

Hoeveel jaar later dan in China zal dit in Nederland het geval zijn? Licht je antwoord toe.

Ultralopen.

Bij hardloopwedstrijden over zeer grote afstanden spreekt men van ultralopen.
De Atletiek Vereniging Texel organiseert om het jaar in de lente een ultraloop over maar liefst 120 km.
De ultraloop van 2005 werd bij de mannen gewonnen door Wim-Bart Knol. Hij legde de afstand af in 9 uur, 53 minuten en 48 seconden. Wij noteren dat in wedstrijdnotatie als 9:53:48.

Bij de vrouwen won Elke Streicher in 11:33:40. Knol liep dus sneller dan Streicher.

5p.

16.

Onderzoek door berekening of de gemiddelde snelheid van Knol meer dan 2 km per uur groter was dan de gemiddelde snelheid van Streicher.

Bij controleposten langs het parcours noteerde men de tussentijden van de atleten. In de volgende tabel zijn de gegevens van Streicher weergegeven.

afstand in km	15	32	45,5	60	74,5	88	105	120
tijd in wedstrijd- notatie	1:18:00	2:47:07	4:04:49	5:35:11	6:59:37	8:19:37	9:58:16	11:33:40
tijd in seconden	4680	10027	14689	20111	25177	29977	35896	41620

De gegevens van deze tabel zijn in de volgende figuur grafisch weergegeven. Daar zie je op de horizontale as de afstand in kilometers en op de verticale as de bijbehorende tijd in uren. De punten A tot en met H corresponderen met de acht uitkomsten uit de tabel. Ook is de lijn getekend die aangeeft hoe de ultraloop zou zijn verlopen wanneer Streicher de hele afstand had gelopen met haar gemiddelde snelheid over de eerste 15 km.

Met behulp van de tabel kun je narekenen dat de gemiddelde snelheid van Streicher gedurende de eerste 15 km hoger was dan gedurende de eerste 88 km. Maar je kunt dat ook zonder berekening zien in de figuur.

3p.

17.

Leg uit hoe je dit zonder berekening uit de figuur kunt afleiden.

In 1997 liep Dirk Westerduin de race met een gemiddelde snelheid van 12,78 km/u. Dit beschouwen we als het record op de afstand 120 km.
Elke wedstrijdafstand s kent een recordtijd. De recordsnelheid die daarbij hoort, noemen we v. Voor elke wedstrijdafstand s kun je dus zeggen: “Het record op de s km werd gelopen met een (gemiddelde) snelheid van v km/u.”
Voor lange afstanden zoals ultralopen kan het verband tussen de afstand s en de recordsnelheid v vrij goed beschreven worden met de formule:

v = c −3,32 • log s

Hierin is c een constante.
Als we deze formule ook willen gebruiken voor korte afstanden, bijvoorbeeld de 100 meter met een toenmalig wereldrecord van 9,77 seconden, dan krijgen we een andere waarde voor de constante c dan bij lange afstanden.

4p.

18.

Laat met een berekening zien dat dit inderdaad het geval is.

Het Doubema.

Bij het 50-jarig bestaan van het Doubemacollege vindt een jubileummarkt plaats. Op deze jubileummarkt staan diverse kraampjes waarbij leerlingen (tegen betaling) spellen kunnen spelen. Bij een van de spellen zijn de foto’s van 7 verschillende leraren van het Doubemacollege opgehangen. Een deelnemer moet onder elke foto een bordje hangen van de favoriete maaltijd van de betreffende leraar. Er liggen namelijk ook 7 bordjes klaar met op ieder bordje de naam van het favoriete gerecht van één van de 7 leraren. Die favoriete gerechten verschillen ook allemaal van elkaar.

We gaan kijken naar de situatie waarin een deelnemer gokt. Hij hangt dus willekeurig bij elke foto één bordje.

Martin denkt dat de 7 bordjes op meer dan 5000 manieren bij de 7 foto’s kunnen worden gehangen.

3p.

19.

Onderzoek of Martin gelijk heeft.

In de volgende tabel staan de kansen dat een deelnemer die gokt, k van de 7 bordjes bij de goede foto hangt. Twee kansen zijn niet ingevuld.

k (aantal goed gehangen bordjes)	0	1	2	3	4	5	6	7
kans P(k) op k goed gehangen bordjes	0,3679	0,3681	0,1833	0,0625	0,0139			0,0002

Die twee ontbrekende kansen kunnen we wel uitrekenen. Je kunt beredeneren dat de kans op 6 goed gehangen bordjes, dus P(6), gelijk is aan 0.

4p.

Beredeneer dat P(6) = 0 en bereken daarmee P(5).

De kans dat een deelnemer die gokt, minder dan 2 bordjes goed hangt, is gelijk aan 0,7360. Dat kun je uit de tabel afleiden.
Veronderstel nu eens dat er 6 mensen deelnemen die allemaal gokken.

3p.

21.

Bereken de kans dat elk van deze 6 deelnemers minder dan 2 bordjes goed hangt.

Ook Jeannette hangt de bordjes in willekeurige volgorde.

3p.

22.

Hoe groot is de kans dat ze 3 of meer bordjes goed heeft gehangen? Licht je antwoord toe.

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

1.	4,5% groei betekent een groeifactor van 1,045 2044 is 40 jaar na 2004. Dan zijn de kosten 4700 • 1,045⁴⁰= 27337 euro

2.	aflezen: de kosten voor het levensonderhoud zullen stijgen tot ongeveer 15500 euro Dat is een factor ¹⁵⁵⁰⁰/₄₇₀₀ = 3,298 dat is een toename van 229,8% ofwel ongeveer 230%

3.	De groei in het vierde jaar is gelijk aan h(4) - h(3) Amerikaanse eik: h = 29,026 • (1 - 0,9790^t)^0,80820 h(4) = 305,5 en h(3) = 382,2 dus in het vierde jaar is de Amerikaanse eik 77 cm gegroeid zomereik: h = 39,143(1 - 0,9867^t)^0,96667 h(4) = 225,2 en h(3) = 171,7 dus in het vierde jaar is de zomereik 54 cm gegroeid. het verschil is 77 - 54 en dat is inderdaad ruim 20 cm

4.	Ze zijn gelijk als 29,026 (1 - 0,9790^t)^0,80820 = 39,143 (1 - 0,9867^t)^0,96667 Voer in de GR in: Y1 = 29,026 * (1 - 0,9790^X)^0,80820 en Y2 = 39,143(1 - 0,9867^X)^0,96667 Intersect geeft dan X = t =* 63 jaar

5.	zomereik: h(t) = a • (1 - 0,9867^t )^0,96667 vul in h = 6,18 en t = 10: 6,18 = a • (1 - 0,9867¹⁰ )^0,96667 ⇒ 6,18 = a • (0,12532)^0,96667 ⇒ 6,18 = a • 0,1343 Þ a = 46,02

6.	h = a(1 - b^t)^cNeem t = 0 dan is h(0) = a(1 - b⁰)^c = a(1 - 1)^c want een getal tot de macht nul is altijd 1. dus h(0) = a • 0^c = a • 0 = 0 dus de grafieken gaan inderdaad allemaal door de oorsprong.

7.	in 2001 waren er 0,333 • 16,0 = 5,328 miljoen rokers die elk 4526 sigaretten rookten. Dat zijn in totaal 24114,528 miljoen sigaretten in 2005 waren er 0,295 • 16,3 = 4,8085 miljoen rokers in Nederland die elk 4271 sigaretten rookten Dat zijn in totaal 20537,1035 miljoen sigaretten. de afname is 24114,528 - 20537,1035 = 3577,4245 miljoen sigaretten Dat is 3577,4245/24114,528 • 100% = 14,8%

8.	Er zijn twee mogelijkheden: F, NF, F, NF, F, NF, F, NF, F, NF geeft kans ⁵/₁₀ • ⁴/₉ • ⁴/₈ • ⁴/₇ • ³/₆ • ³/₅ • ²/₄ • ²/₃ • ¹/₂ • 1 = ¹/₂₅₂= 0,004 (of: er zijn 10 nCr 5 = 252 mogelijkheden, waarvan 1 gunstig, dus de kans is ¹/₂₅₂)

9.	De kans dat één persoon géén F-tablet inneemt is 0,5 De kans dat 18 mensen dat doen is dan 0,5¹⁸ = 4 • 10^-6 = 0,000004

10.	Voor één persoon is die kans 0,2. Het aantal proefpersonen dat de eerste dag tablet 1 of 2 kiest is binomiaal verdeeld. Het aantal experimenten is n = 18. De kans op succes (1 of 2 kiezen) per keer is 0,2 Het gaat om 6 of meer successen, dus P(X ≥ 6) = 1 - P(X ≤ 5) = 1 - binomcdf(18, 0.2, 5) = 0,133

11.	normalcdf(20, 10000..., 11.4, X) = 0,245 voer in de GR in: Y1 = normalcdf(20, 100000, 11.4, X) en Y2 = 0,245 intersect geeft X = σ = 11,7 Als het gemiddelde 11,4 is, dan kan de standaardafwijking nooit 11,7 zijn, want dat zou betekenen dat een aantal rokers minder dan nul sigaretten per dag zou roken! Daarom zal het aantal sigaretten niet normaal verdeeld zijn.

12.	2 mensen in dienst gaf in totaal 1298 personeelsleden, dus dat waren 1298/2 = 649 salons. In totaal waren er 10820 salons, dus dat is 649/10820 • 100% = 6%

13.	De toename is 10820 - 6800 = 4020 salons Dat gebeurde in 10 jaar dus per jaar is de toename 402 salons. Tot 2012 is nog 7 jaar, dus zal de toename 7 • 402 = 2814 salons zijn. Het aantal in 2012 is dan 10820 + 2814 = 13634

14.	Als de grafieken op dezelfde schaal worden getekend, dan moet de linkerschaal nogal uitgerekt worden om gelijk te worden aan de rechterschaal. Maar als je een grafiek verticaal uitrekt, dan wordt de helling groter. Dus zullen de hellingen bij gelijke schaal niet meer hetzelfde zijn (de helling van A zal groter zijn)

15.	1 op de 500 betekent 50 salons op de 25000 mensen. Nederland: 50 = 17 + 0,6t 0,6t = 33 t = 55 (dus in 2060) China: 50 = 30,8 • 1,06^t 1,06^t = 1,623... t = ^{LOG(1,623...)}/_LOG(1,06)= 8,3 (dus in 2013) In Nederland zal het dus 47 jaar later zijn dan in China.

16.	Knol liep 9 uur + 53/60 uur + 48/3600 uur, en dat is 9,89666 uur over de 120 km. Zijn snelheid was dus ¹²⁰/_9,89666= 12,13 km/uur Streicher liep 11 uur + ³³/₆₀ uur + 40/3600 uur, en dat is 11,56111 uur over de 120 km Haar snelheid was dus ¹²⁰/_11,56111 = 10,38 km/uur Dus Knol liep 12,13 - 10,38 = 1,75 km/uur harder en dat is minder dan 2 km/uur.

17.	De snelheid vanaf het begin tot een bepaald punt van de grafiek wordt gegeven door de helling van de lijn vanaf de oorsprong naar dat punt. Hiernaast zie je dat de rode lijn OF een grotere helling heeft dan de blauwe OA, dus een grotere snelheid.

18.	100 meter is 0,1 km 9,77 seconden is ^9,77/₃₆₀₀ uur = 0,002713.. uur De snelheid is dus v = ^0,1/_0,002713... = 36,847... km/uur. Invullen in de formule geeft 36,847 = c - 3,32 • log(0,1) Daaruit volgt c = 36,847 + 3,32 • log(0,1) = 33,53 Voor de 120 km geldt: 12,78 = c - 3,32 • log(120) dus c = 12,78 + 3,32 log(120) = 19,68 Dat is inderdaad verschillend.

19.	Voor het eerste bordje zijn 7 mogelijkheden, voor het tweede nog 6, voor het derde 5, enz. In totaal zijn er 7 • 6 • 5 • 4 • 3 • 2 • 1 = 7! = 5040 mogelijkheden. Martin heeft dus gelijk.

20.	Als er zes bordjes goed hangen, dan moet het zevende bordje ook wel goed hangen, dus hangen er dan automatisch 7 goed. Precies zes kan dus niet, dus is de kans erop nul. Alle kansen samen zijn altijd 1 (100%) De kansen uit de tabel zijn samen al 0,9959 Daar moet dus nog 0,0041 voor P(5) bijkomen (P(6) is immers 0).

21.	0,7360⁶ = 0,159.

22.	P(3 of meer goed) = P(3) + P(4) + P(5) + P(6) + P(7) = 0,0625 + 0,0139 + 0,0041 + 0 + 0,0002 = 0,0807
	(als je P(5) niet hebt gevonden kan het ook door te bedenken dat P(3 of meer) = 1 - P(minder dan 3) = 1 - P(2) - P(1) - P(0) )