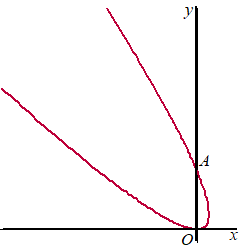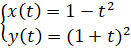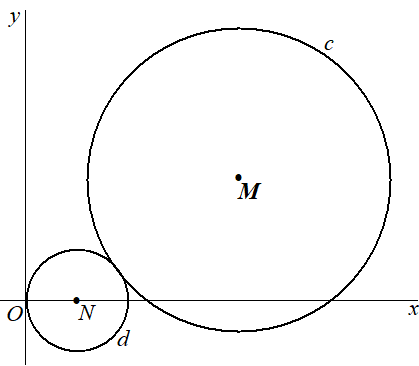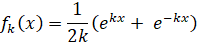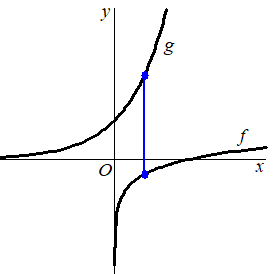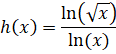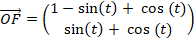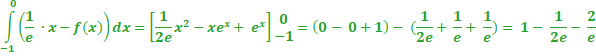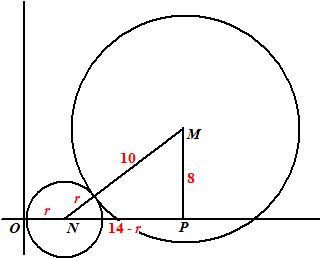VWO WB, 2018 - I

 

Bewegend punt.
       

De beweging van een punt P wordt gegeven door de volgende
bewegingsvergelijkingen:

     

     

In de figuur is de baan van P weergegeven.
     

De baan van P snijdt de y-as in de oorsprong O en in punt A.  Zie de figuur.
       

4p.

1.

 Bereken exact de snelheid waarmee P door punt A gaat.
       
Voor elke waarde van t bevindt P zich op de kromme met vergelijking:  (x + y)2 = 4y
       

4p.

2.

 Bewijs dit.
       
Lijn door de toppen.
       

Voor elke waarde van a met a > 0 wordt de functie fa gegeven door  fa(x) = xeax

De afgeleide functie fa' wordt gegeven door  fa'(x) = eax+ axeax
In onderstaande figuur zie je voor een aantal waarden van a de grafiek van fa.

Ook is de lijn l met vergelijking  y = 1/e • x  weergegeven.
       

       

Voor elke waarde van a met a > 0 heeft de grafiek van fa precies één top.
       

4p.

3.

 Bewijs dat deze top op lijn l ligt.
       
De functie Fa is gegeven door:

       
Fa is een primitieve van fa .
       

3p.

4.

 Bewijs dat Fa inderdaad een primitieve van fa is.
       

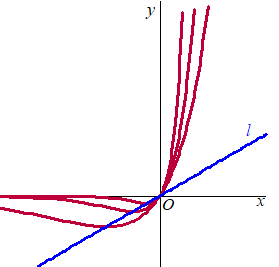
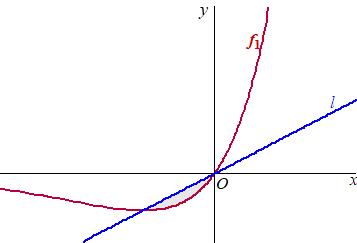
Voor f1 geldt f1(x) = xex . In de volgende figuur is de grafiek van f1 getekend, en ook lijn l. Het vlakdeel tussen lijn l en de grafiek van f1 is grijs gemaakt.
       

       

5p.

5.

 Bereken exact de oppervlakte van het grijze vlakdeel.
       
Zwaartepunt en rakende cirkels.
       

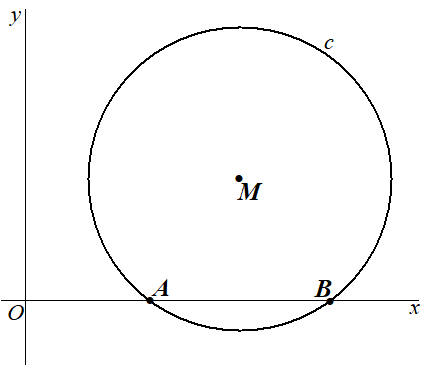
Gegeven is cirkel c met middelpunt M(14, 8) en straal 10. Deze cirkel snijdt de x-as in de punten A en B met xA < xB .
Zie de figuur. In A bevindt zich een puntmassa met massa 3, in B een puntmassa met massa 1 en in M een puntmassa met massa 2.
       

       

5p.

6.

Bereken exact de coördinaten van het zwaartepunt van deze drie puntmassa’s.
       

De cirkel d met middelpunt N raakt de y-as in de oorsprong O en raakt cirkel c zoals weergegeven in onderstaande figuur.
       

       

5p.

7.

 Bereken exact de straal van cirkel d.
       
Maxima en minima
       

De functie f wordt gegeven door f (x) = 6sin(x) - cos(2x) .

De grafiek van f  heeft oneindig veel toppen.
       

6p.

8.

 Bereken exact de x-coördinaten van alle toppen van de grafiek van f.
       

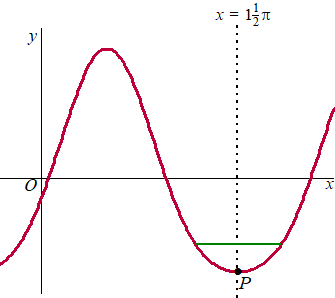
Een van de toppen is het punt P(11/2π, -5).
De grafiek van f  is symmetrisch ten opzichte van de verticale lijn door P.

Boven P wordt een horizontaal lijnstuk van lengte 2 geplaatst, waarvan de eindpunten op de grafiek van f  liggen. Zie de figuur.
       

       

4p.

9.

Bereken de afstand van P tot het horizontale lijnstuk. Rond je eindantwoord af op twee decimalen.
       
Sheffield Winter Garden
       
Voor elke waarde van k met k > 0 wordt de functie fk gegeven door:
       

       
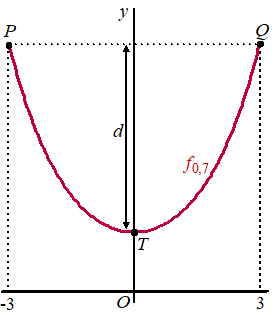
De grafiek van fk wordt een kettinglijn genoemd.

Op de grafiek van fk worden twee punten P en Q met gelijke y-coördinaat gekozen. De lengte van het deel van de kettinglijn tussen P en Q noemen we l. De top T van de kettinglijn ligt op de y-as. De afstand van T tot de horizontale lijn PQ noemen we d. Zie de figuur.
     

     

In de figuur is voor k = 0,7 , xP = -3 en xQ = 3 het bijbehorende deel van de kettinglijn getekend.
     

4p.

10.

Bereken voor de situatie van deze figuur de lengte van het deel van de kettinglijn tussen P en Q.
Rond je eindantwoord af op twee decimalen.
       

Als het deel van de grafiek van fk  tussen P en Q wordt gespiegeld in de x-as en vervolgens omhoog wordt geschoven, ontstaat een boog.

Bij de bouw van de Sheffield Winter Garden, een in 2003 geopende plantenkas, is gebruikgemaakt van dergelijke bogen. Zie de foto.
       

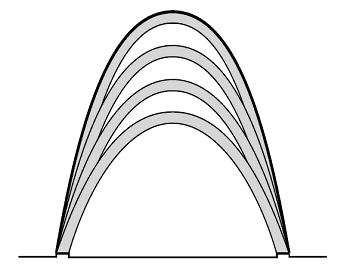
De ontwerpers hebben een tekening gemaakt van het vooraanzicht van het gebouw. Dit vooraanzicht bestaat uit acht bogen. Zie de figuur hiernaast. In de rest van deze opgave kijken we naar de grootste boog. Deze boog is in de figuur hiernaast  dikker gedrukt.

 

Voor de grootste boog in deze tekening geldt:
-  de lengte van de boog is 49,63 meter;
-  het hoogste punt van de boog bevindt zich 20,51 meter boven de grond.

Bij deze grootste boog gaan we een functievoorschrift opstellen.
We kiezen daartoe een assenstelsel waarbij de x-as door de onderste punten van de boog gaat en de top van de boog op de y-as ligt. De eenheden langs de assen zijn meters.

In dit assenstelsel wordt de boog weergegeven door de grafiek van een functie h.
De grafiek van deze functie h ontstaat door de grafiek van een functie fk te spiegelen in de x-as en de beeldgrafiek vervolgens omhoog te schuiven.

Er is precies één waarde van k waarvoor de beeldgrafiek de juiste lengte en hoogte heeft.
       

5p.

11.

Stel een functievoorschrift op van h. Rond de getallen in je eindantwoord af op twee decimalen.
       
Natuurlijke logaritme van de wortel.
       

De functie f wordt gegeven door f (x) = ln (√x).

Deze functie heeft een inverse functie f inv . Er geldt: f inv(x) = e2x .
       

3p.

12.

 Bewijs dat inderdaad geldt  f inv (x) = e2x.
       

De grafiek van f inv wordt ten opzichte van de x-as met factor 1/2 vermenigvuldigd. Zo ontstaat de grafiek van de functie g.
Elke verticale lijn rechts van de y-as snijdt de grafiek van f in één punt en de grafiek van g in één punt. Het lijnstuk tussen deze twee punten heeft een lengte die afhangt van de plaats van de verticale lijn. Zie de figuur.
       

       

4p.

13.

Bereken de minimale lengte van het lijnstuk. Rond je eindantwoord af op drie decimalen.
       
De functie h wordt gegeven door:

       
De grafiek van h heeft rechts van de y-as één perforatie.
       

4p.

14.

 Bereken exact de coördinaten van deze perforatie.
       
Vierkant onder grafiek.
       

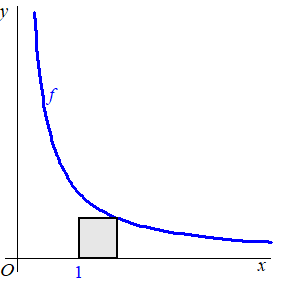
Voor x > 0 wordt de functie f gegeven door  f(x) = 1/x

In de figuur is de grafiek van f getekend. Onder de grafiek is een vierkant getekend met twee zijden evenwijdig aan de x-as en twee zijden evenwijdig aan de y-as.
       

       

Het vierkant heeft linksonder hoekpunt (1, 0) . Het hoekpunt rechtsboven ligt op de grafiek van f.
       

4p.

15.

 Bereken exact de lengte van de zijde van het vierkant.
       
Twee vierkanten op een kwartcirkel.
       

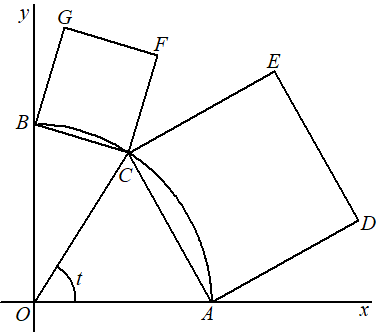
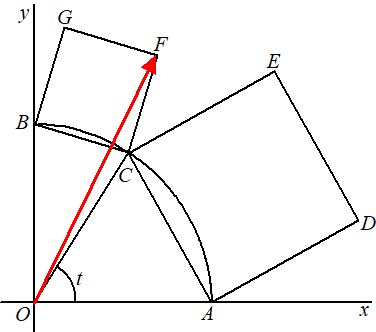
Gegeven zijn de punten A(1, 0) en B(0,1). Punt C bevindt zich op de kwartcirkel door A en B met middelpunt O(0, 0) . Op de lijnstukken AC en BC worden twee vierkanten ADEC en BCFG getekend. Zie de volgende figuur.
       

       

De grootte van hoek AOC (in radialen) noemen we t, met  0  ≤  t  ≤  1/2π.
Punt C heeft dus coördinaten (cos(t), sin(t)) .

Er is een waarde van t waarvoor de oppervlakte van vierkant ADEC twee keer zo groot is als de oppervlakte van vierkant BCFG.
       

5p.

16.

 Bereken deze waarde van t. Rond je eindantwoord af op twee decimalen.
       

In de onderstaande figuur is de situatie van de vorige figuur uitgebreid met vector OF.
       

       

Voor elke waarde van t met   0  ≤  t  ≤  1/2π  geldt:

       

4p.

17.

 Bewijs dit.
       

 

 

 

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. Voor punt A geldt  x = 0  dus  1 - t2 = 0
Dat geeft t = 1  ∨  t = -1
t = -1 geeft punt (0, 0) dus dat is niet A. Bij A hoort dus t = 1.

x' = -2t  dus voor t = 1 is  x' = vx = -2
y' = 2(1 + t) dus voor t = 1 is  y' = vy = 4
v = √(vy2 + vx2) = √((-2)2 + 42) = √20 = 2√5
   
2. (x + y)2
= (1 - t2 + (1 + t)2)2
= (1 - t2 + 1 + 2t + t2)2
= (2 + 2t)2
= 4 + 8t + 4t2
= 4(t2 + 2t + 1)
= 4(t + 1)2
= 4y
qed.
   
3. voor de top geldt  f ' = 0
 fa'(x) = eax+ axeax  = 0
eax (1 + ax) = 0
eax = 0  ∨  1 + ax = 0
ax = -1   (want eax kan niet nul zijn)
x = -1/a
y =  xeax = x • e-1  = 1/e • x   (want ax = a • -1/a = -1)
   
4. Dat kun je het handigst doen door F te differentiëren en te laten zien dat daar f uitkomt.
Denk om de productregel bij het eerste deel:
 

 

   
5. snijpunt:  xex = 1/e• x
xex + 1/e • x = 0
x(ex - e-1) = 0
x = 0  ∨  ex = e-1
x = 0  ∨  x = -1
Voor a = 1  is  F = xex - ex
De oppervlakte is de integraal van de bovenste min de onderste, dus l - f:
 

   
6. M(14, 8) en straal 10 geeft vergelijking  (x - 14)2 + (y - 8)2 = 100
y = 0  geeft dan  (x - 14)2 + 64 = 100
(x - 14)2 = 36
x - 14 = 6  ∨  x - 14 = -6
x = 20  ∨  x = 8
A = (8, 0) en heeft gewicht 3
B = (20,0) en heeft gewicht 1
M = (14,8) en heeft gewicht 2
xZ = (3 • 8 + 1 • 20 + 2 • 14)/6 = 12
yZ = (3 • 0 + 1 • 0 + 2 • 8)/6 = 8/3
Z = (12, 8/3)
   
7.
  Zie de figuur waarin P de projectie van M op de x-as is.
NP = OP - ON = 14 - r
Pythagoras in driehoek MPN:   (10 + r)2 = (14 - r)2 + 64
100 + 20r + r2 = 196 - 28r + r2 + 64
48r = 160
r = 31/3
   
8. f (x) = 6sin(x) - cos(2x)
f ' = 6cosx + 2sin(2x) = 0
6cosx + 2 • 2sinxcosx = 0
cosx(6 + 4sinx) = 0
cosx = 0  ∨  6 + 4sinx = 0
cosx = 0  ∨  sinx = -11/2  (en dat laatste heeft geen oplossing)
x = 1/2π + k2π  ∨  x = -1/2π + k2π
samen te vatten als  x = 1/2π + kπ
   
9. Het lijnstuk heeft lengte 2, dus loopt van x = 11/2π - 1 tot z = 11/2π + 1
f(11/2π - 1) = -3,6579....
de top ligt bij  y = -5, dus de afstand is 1,34.
   
10. x = 0  geeft  f(x) =  1/(2 • 0,7) • (e0,7 • 0 + e-0,7• 0) = 1,42857....
x = 3  geeft  f(x) = 1/(2 • 0,7) • (e0,7 • 3 + e-0,7 • 3) = 5,9204....
Dus  d = 5,9204... - 1,42857... = 4,49187....

0,7 = 8 • 4,49187/(l2 - 4 • 4,49187...2)
0,7 = 35,935/(l2 - 80,708)
l2 - 80,708 = 35,935/0,7 = 51,336
l2 = 132,044
l = 11,49
   
11. d = 20,51 en l = 49,63 geeft  k = 8 • 20,51/(49,632 - 4 • 20,512) = 0,210225....
Dus  f(x) = 2,37... • (e0,21x + e-0,21x)
Dan is f(0) = 4,756...
Spiegelen in de x-as geeft  top bij  y = -4,756... en die moet omhoog geschoven worden naar y = 20,51
Dat is over een afstand 25,2668....

een functievoorschrift voor h is dan  h(x) = - 2,38 • (e0,21x + e-0,21x) + 25,27
(het minteken vanwege het spiegelen, de +25,27 vanwege het omhoog schuiven)
   
12. y = ln(√x)
ga nu voor de inverse  x en y verwisselen
x = ln(√y)
ex =  √y
y = (ex)2 = e2x
   
13. g(x) = 1/2 • e2x  en  f(x) = ln(√x)
de lengte is  L = g - f = 1/2 • e2x  - ln(√x)
voer deze formule in  bij Y1 van de GR en gebruik calc - minimum
dat geeft een minimum van 1,512  (bij x = 0,28357)
   
14. er is een perforatie als de formule 0/0 geeft en te vereenvoudigen is.
dat moet dan zijn als lnx = 0  dus als x = 1
de vereenvoudiging:
 
  De perforatie is dus  (1, 1/2)
   
15. Als het vierkant zijde a heeft, dan is de hoogte dus ook a
Dan moet gelden  f(1 + a) = a want het punt rechtsboven ligt op de grafiek van f.
1/(1 + a) = a
1 = a(1 + a)
1 = a + a2
a2 + a - 1 = 0
a = (-1 ± √5)/2  = -1/2 + 1/2√5   (de - valt af want ligt niet rechts van de y-as)
   
16. A = (1, 0) en C = (cost, sint)  dus  AC2 = (cost - 1)2 + sin2t   en dat is de oppervlakte van ADEC
B = (0, 1) en C = (cost, sint) dus BC2 = cos2t + (sint - 1)2  en dat is de oppervlakte van CFGB

De ene is tweemaal de andere:
2 • (cos2t + (sint - 1)2) = (cost - 1)2 + sin2t 
2 • (cos2t + sin2t - 2sint + 1) = cos2t - 2cost + 1 + sin2t 
maar cos2t + sin2t = 1 dus dan wordt dat:
2 • (2 - 2sint) = 2 - 2cost
4 - 4sint = 2 - 2cost
invoeren bij Y1 en Y2 in de GR en dan intersect.
Dat geeft t ≈ 0,93
   
17.
  voor CF moet je BC 90º tegen de klok in draaien