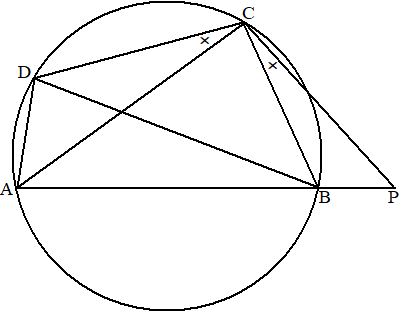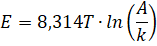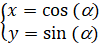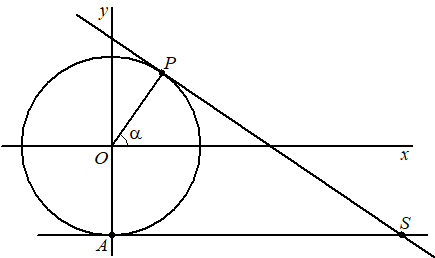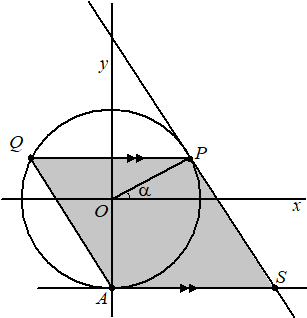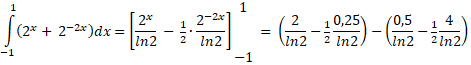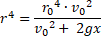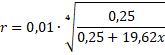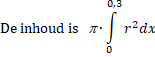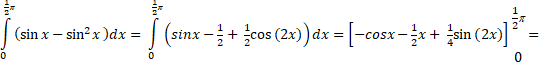VWO WB, 2017 - II

 

Twee  machten van 2.
       

 
De functie f  is gegeven door:

f (x) = 2x + 2-2x

In de figuur hiernaast  is een deel van de grafiek van f weergegeven.
De functie heeft ιιn extreme waarde
en dat is een minimum.

     
5p.

1.

 Bereken exact de waarde van x waarvoor f(x) minimaal is.
     

 

In de figuur linksonder  is het gebied grijs gemaakt dat wordt begrensd door de grafiek van f , de x-as en de lijnen met vergelijkingen x = -1 en x = 1. In de figuur rechtsonder is het rechthoekige gebied grijs gemaakt dat wordt begrensd door de x-as en de lijnen met vergelijkingen x = -1, x = 1 en y = k .
De waarde van k is zo gekozen dat het grijze gebied uit beide figuren dezelfde oppervlakte hebben.
       

       
5p.

2.

Bereken algebraοsch de waarde van k. Rond je eindantwoord af op twee decimalen.
     

 
De stelling van Ptolemaeus.
       

De Griekse wiskundige Ptolemaeus leefde van 87 tot 150 na Christus.
In een van zijn stellingen formuleert hij het volgende verband tussen de lengtes van de twee diagonalen en de vier zijden van een koordenvierhoek ABCD:

AC • BD = AB • CD +  AD • BC

In deze opgave gaan we deze stelling van Ptolemaeus in stappen bewijzen.

In de figuur is een koordenvierhoek ABCD getekend. Verder is op het verlengde van zijde AB, aan de kant van B, punt P getekend waarvoor geldt: ∠ACD = ∠PCB.
       

       
De driehoeken ACD en PCB zijn gelijkvormig.
       
4p.

3.

 Bewijs dit.  
     

 
Ook de driehoeken BCD en PCA zijn gelijkvormig
       
4p.

4.

 Bewijs dit.  
     

 

Uit de gelijkvormigheid van de driehoeken BCD en PCA volgt de uitdrukking

AP • CD =  AC • BD

Uit de gelijkvormigheid van de driehoeken ACD en PCB volgt voor BP • CD een soortgelijke uitdrukking.
       
4p.

5.

Bewijs met behulp van deze uitdrukkingen de stelling van Ptolemaeus:
AC • BD = AB • CD  +  AD • BC
     

  
Straal van een waterstraal.
       

In deze opgave kijken we naar water dat uit een cirkelvormige
kraanopening stroomt.

In de figuur hiernaast is de vorm van de waterstraal getekend. Op elke hoogte is de horizontale doorsnede van de waterstraal een cirkel. De straal van die cirkel wordt naar beneden toe steeds kleiner.

Op hoogte h heeft de horizontale doorsnede straal r en is de stroomsnelheid van het water v.
De kraanopening heeft straal r0 en bevindt zich op hoogte h0.
De snelheid waarmee het water uit de kraan stroomt, is v0.
Het hoogteverschil h0 - h geven we aan met x.

In de formules van deze opgave is meter de eenheid van lengte en meter per seconde de eenheid van snelheid.

Uit de (natuurkundige) Wet van behoud van energie volgt:
v02  + 2gh0  =  v2  +  2gh      .....(1)

Hierin is g de valversnelling van 9,81 m/s².

De hoeveelheid water die per seconde op een bepaalde hoogte voorbijstroomt, is voor elke hoogte gelijk. Hieruit is af te leiden:
r02 • v0  =  r2 •  v       .....(2)

Door formule 1 en formule 2 te combineren kan worden aangetoond:
   

 

  
       
5p.

6.

 Toon door formule 1 en formule 2 te combineren aan dat formule 3 juist is.
     

 

Een bepaalde kraan heeft een opening met een diameter van 2 cm. De opening bevindt zich 30 cm boven een oppervlak. De kraan wordt zo ver opengedraaid dat v0 = 0,5 m/s.

In onderstaande figuur is voor deze waterkraan de grafiek getekend die het verband weergeeft tussen het hoogteverschil x en de straal r.
       

       

Als deze grafiek wordt gewenteld om de horizontale x-as, ontstaat de vorm van de waterstraal (90 graden linksom gedraaid).

De inhoud van het omwentelingslichaam is gelijk aan de hoeveelheid water waaruit de waterstraal op een bepaald moment bestaat.
       
5p.

7.

Bereken deze hoeveelheid. Rond je eindantwoord af op een geheel aantal cm3.
     

  
Sinus en het kwadraat van sinus.
       

Voor 0 ≤ x ≤ 1/2π  zijn de functies f en g gegeven door f (x) = sin(x) en  g(x) = sin2(x) . De grafieken van f en g snijden elkaar in O en (1/2π, 1)

V is het vlakdeel dat wordt begrensd door de twee grafieken.
In de volgende figuur is V grijs gemaakt.
       

       
5p.

8.

 Bereken exact de oppervlakte van V.
     

 

De lijn met vergelijking x = p , met 0 < p <  1/2π,  snijdt de grafiek van f  in het punt A en die van g in het punt B. Zie onderstaande figuur

       

       
De lengte van lijnstuk AB is afhankelijk van p.
       
6p.

9.

 Bereken exact de maximale lengte van lijnstuk AB.
     

 
De vergelijking van Arrhenius.
       

Om een chemische reactie tot stand te brengen is een bepaalde hoeveelheid activeringsenergie nodig. De Zweedse scheikundige en Nobelprijswinnaar Svante Arrhenius heeft een vergelijking opgesteld die het verband aangeeft tussen het aantal reagerende moleculen, de temperatuur en de activeringsenergie:

     

     
Hierin is:

-
-
-
-

A de constante van Arrhenius;
E de activeringsenergie (in joule per mol);
T de temperatuur (in kelvin);
k een getal dat aangeeft hoeveel moleculen er per seconde reageren.
       
De vergelijking van Arrhenius kun je herleiden tot de volgende vorm:
       

       
4p.

10.

 Geef een herleiding waaruit dit blijkt.
     

 

E en A hebben voor elk soort reactie een eigen waarde. De waarden van E en A hangen niet af van de temperatuur. Omdat ze niet direct te meten zijn, meet men bij een reactie de waarde van k bij twee verschillende temperaturen. Hieruit zijn dan met de vergelijking van Arrhenius de bij die reactie horende waarden van E en A te berekenen.

Als voorbeeld bekijken we de chemische reactie waarbij stikstofdioxide wordt omgezet naar stikstofmonoxide en zuurstof.
Voor deze reactie is in een proef vastgesteld dat k = 2,7·10–2 als T = 500 en dat k = 2,4·10–1 als T = 550.
       
3p.

11.

Bereken de waarde van E van deze reactie. Geef je eindantwoord in de vorm a • 105 , met a afgerond op ιιn decimaal.
     

 
Op een cirkel.
       

Op de cirkel met middelpunt O(0, 0) ligt punt A(0, -1).
Punt P beweegt over de cirkel volgens de bewegingsvergelijkingen:
 

       

waarbij α  (met  0 < α  < 1/2π) de draaihoek in radialen is ten opzichte van de positieve x-as.
     
     

De raaklijnen aan de cirkel in de punten A en P snijden elkaar in een punt S. In de figuur hiernaast is een mogelijke situatie getekend.

Voor de x-coφrdinaat van S geldt:
     

     
7p. 12. Bewijs dit.
   

 

Punt Q op de cirkel is het beeld van P bij spiegeling in de y-as. Als P over de cirkel beweegt, veranderen de posities van Q en van S. Bij deze beweging blijven de lijnstukken AS en PQ evenwijdig.

Voor  0 < α  < 1/2π is er een positie van P waarbij de lijnstukken PQ en AS even lang zijn.

Hiernaast is deze situatie getekend.

     
8p.

13.

 Bereken voor deze situatie exact de omtrek van vierhoek ASPQ.
     

 
Middelloodlijn en Koordenvierhoek.
       

Gegeven is een scherphoekige driehoek ABC waarin de middelloodlijn van AB zijde BC snijdt. De cirkel door de punten A, B en C heeft als middelpunt M. De middelloodlijn van AB gaat dus door M. Deze middelloodlijn snijdt AB in punt R en BC in punt S. Zie de figuur.
In de figuur is ook vierhoek AMSC aangegeven.
       

       
6p.

14.

 Bewijs dat vierhoek AMSC een koordenvierhoek is.
     

  

 

 

UITWERKING
   
Het officiλle (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. Dan is de afgeleide nul.
f ' = 2x • ln2 + 2-2x • ln2 • -2 = 0
ln2 • (2x - 2 • 2-2x) = 0
2x - 2 • 2-2x = 0
2x  = 2 • 2-2x
2x = 2-2x + 1 
x = -2x + 1
3x = 1
x = 1/3.
   
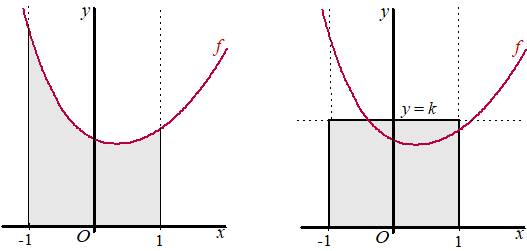
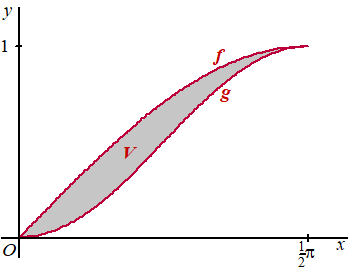
2. De oppervlakte in de linkerfiguur:
 

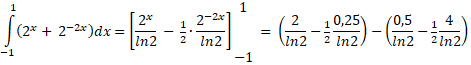  = 1/ln2 • (2 - 1/8 - 1/2 + 2) = 1/ln2 • 27/8 ≈ 4,8691
  De oppervlakte rechts is  2k
2k = 4,8691  geeft  k ≈ 2,43
   
3. ∠ABC = 180Ί- ∠ADC  (koordenvierhoek)
∠PBC = 180Ί- ∠ABC  (gestrekte hoek)
Dus  ∠PBC = ∠ADC

Dus zijn de driehoeken gelijkvormig (hh)
   
4. Als de driehoeken gelijkvormig zijn, dan zijn ook de rode hoeken BPC en DAC hiernaast gelijk.

Maar ook ∠DAC = ∠DBC (constante hoek)
Dus ∠DBC = ∠APC

∠DCB = kruisje plus ∠ACB
∠ACP = kruisje plus ∠ACB
Dus ∠DCB = ∠APC

Dus zijn de driehoeken gelijkvormig (hh)
 
   
5.

Uit de gelijkvormigheid van ACD  en  PCB volgt:   BP/BC  = DA/DC  dus  BP • DC = DA • BC   ....(1)

Gegeven is  AP • CD = AC • BD
Maar AP = AB + BP  dus  dat wordt  (AB + BP) • CD = AC • BD   ofwel  AB • CD + BP • CD = AC • BD
Vervang BP • CD door (1)  dan krijg je  AB • CD + DA • BC = AC • BD
Dat is precies de stelling van Ptolemaeus.

   
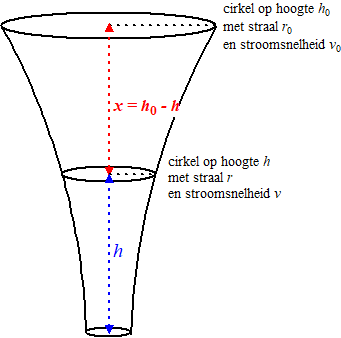
6.

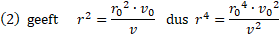  Die v2 in de noemer kunnen we met vergelijking (1) vervangen: 
v2 = v02 + 2gh0 - 2gh = v02 + 2g(h0 - h) = v02 + 2gx
invullen in de vergelijking. voor r4:
 

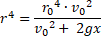  Neem van beide zijden de vierdemachtswortel en je hebt de gevraagde vergelijking.
   
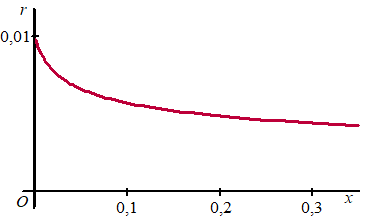
7. v0 = 0,5  en  h = 0,3 en  r0 = 0,01 geeft: 
 

 

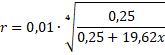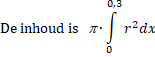  Y1 = 0,01 * (0,25/(0,25 + 19,62 * X))^0,25
Y2 =  π * Y1^2
 2nd - calc -  ∫f(x)dx van Y2 met  lower limt X = 0  en upper limit  X = 3 geeft inhoud 3,1658... • 10-5  m3
Dat is ongeveer  32 cm3
   
8. sin2x = 1/2 - 1/2cos(2x)  want dat volgt uit de verdubbelingsformule van cos(2x)
 

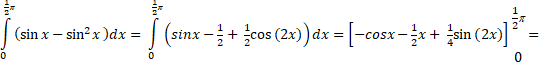  = (-0 - 1/4π + 0) - (-1 - 0 + 0)  = 1 - 1/4π
   
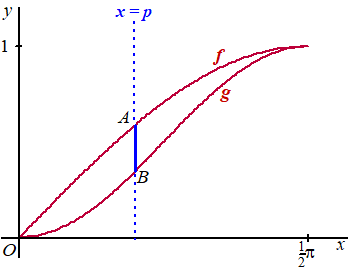
9. Voor de lengte L geldt  L = sinx - sin2x
Dat is maximaal als de afgeleide ervan nul is:
L' =  cosx - 2sinx • cosx = 0
cosx(1 - 2sinx) = 0
cosx = 0  ∨   1 - 2sinx = 0
cosx = 0  ∨ sinx = ½
tussen 0 en ½π  geeft dat  x = ½π  ∨  x = 1/6π 
De gezochte waarde is de laatste (bij de eerste is de lengte minimaal)
dat geeft  Lmax = 1/2 - (1/2)2 = 1/4
   
10.

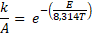  Neem van beide kanten de natuurlijke logaritme:   ln(k/A) = -(E/8,314T)
E/8,314T = -ln(k/A) = ln((k/A)-1) = ln(A/k)
vermenigvuldig met 8,314T:    ln(A/k) • 8,314T = E 
   
11. T = 500 en  k = 2,7 • 10-2  geeft   E = 4157 • ln(37,03A)
T = 550  en  k = 2,4 • 10-1   geeft  E = 4572,7 • ln(4,167A)
gelijkstellen:   4157 • ln(37,03A) = 4572,7 • ln(4,167A)
Y1 = 4157 * ln(37,03*X)
Y2 = 4572,7 * ln(4,167*X)
calc - intersect levert  E = Y = 1,0 • 105  J/mol 
   
12.
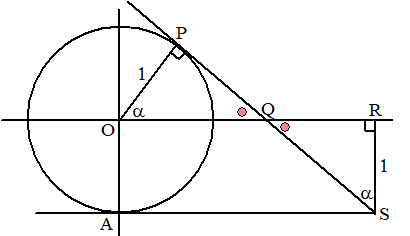  ∠OPS = 90Ί  (raaklijn aan cirkel)
∠OQP = SQR  (overstaande hoeken)
Dus is ∠QSR = a
In driehoek OPQ:   cosa = 1/OQ  dus  OQ = 1/cosa
in driehoek QRS:  tana = QR/1 dus QR = tana

OR = OQ +  QR = 1/cosa + tana = 1/cosa +  sina/cosa = (1 + sina)/cosa
   
13. AS = (1 + sina)/cosa
PQ = 2 • cosa
Die zijn gelijk als  (1 + sina)/cosa = 2cosa
1 + sina = 2cos2a
1 + sina = 2(1 - sin2a)
1 + sina = 2 - 2sin2a
2sin2a + sina - 1 = 0
ABC-formule:  sina = (-1 ± √(1 + 8))/4  = 1/2  of  -1  (maar die laatste vervalt)
sina = 1/2  geeft  a = 1/6π
AS = QP = 2cosa = 2 • 1/2√3 = √3
Q = (-1/2√3, 1/2)  en  A = (0, -1)  dus  AQ2 = (1/2√3)2 + (3/2)2 = 3  dus  AQ = √3
De omtrek is dan   2√3 + 2√3 = 4√3
   
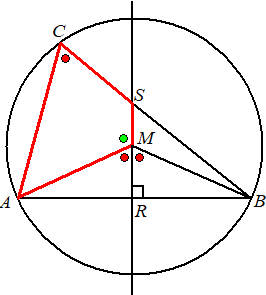
14. MR is middelloodlijn van AB dus AR = RB
MR = MR
Dus driehoek AMB is gelijkbenig met gelijke basishoeken
Dus AMR en BMR zijn gelijkvormig  (ZZR)
Dus is ∠AMR = ∠BMR

Maar ∠ACB = 1/2 • ∠AMB  (koorde AB) 
Dus ∠ACB = ∠AMR

Rood plus groen hiernaast is 180Ί (gestrekte hoek bij M
Dus ∠ACS + ∠AMS = 180Ί

Dan is AMSC een koordenvierhoek.