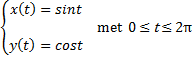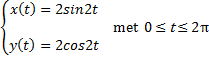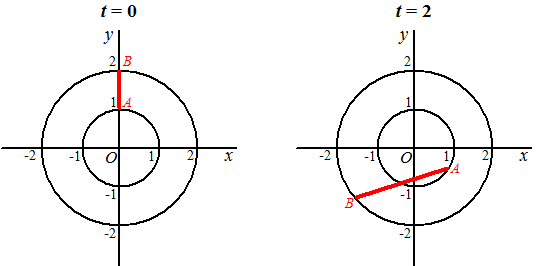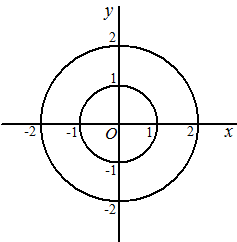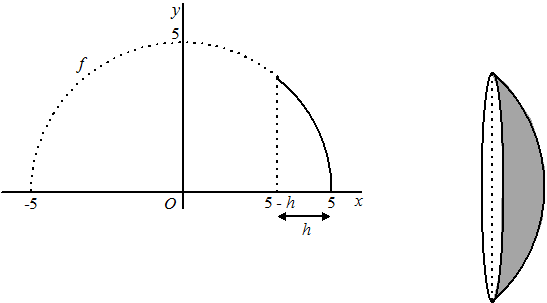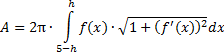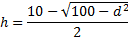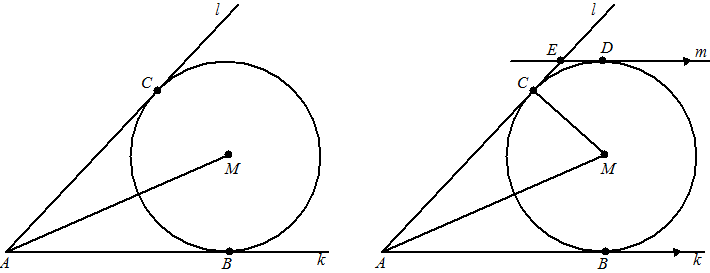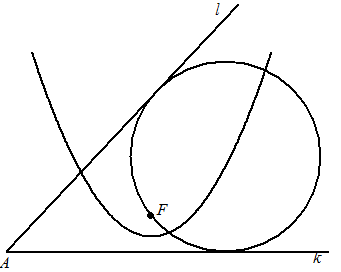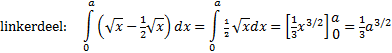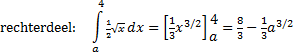VWO WB, 2015 - I

 

Wortelfuncties
       
In de figuur zijn de grafieken getekend van de functies f en g gegeven door  f(x) = √x  en  g(x) = 1/2√x.
Verder zijn de lijnen getekend met vergelijkingen x = a  en  x = 4  met  0 < a < 4.
       

       
In de figuur zijn twee vlakdelen grijs gemaakt. Het ene grijze vlakdeel wordt begrensd door de grafieken van f en g en de lijn met vergelijking x = a. Het andere grijze vlakdeel wordt begrensd door de grafiek van g, de x-as en de lijnen met vergelijkingen x = a  en  x = 4.
       
6p. 1. Bereken exact voor welke waarde van a deze vlakdelen gelijke oppervlakte hebben.
     

   
Cirkels en lijnstuk.
       
Over de cirkel met middelpunt (0,0) en straal 1 beweegt een punt A met bewegingsvergelijkingen:
       

       
Over de cirkel met middelpunt (0,0) en straal 2 beweegt een punt B met bewegingsvergelijkingen:
       

       
In de figuren hieronder zijn de twee cirkels en het lijnstuk AB getekend voor de tijdstippen t = 0  en  t = 2.
       

       
Op de tijdstippen waarop B zich op de x-as bevindt, bevindt A zich op de lijn met vergelijking y = x of op de lijn met vergelijking y = -x.
       
5p. 2. Bewijs dit.  
     

 

In onderstaande figuur is het lijnstuk AB getekend op een tijdstip waarop het horizontaal is en boven de x-as ligt.
       

       
Er zijn twee tijdstippen waarop het lijnstuk AB horizontaal is en onder de x-as ligt.
       
6p. 3. Bereken voor één van deze tijdstippen de coördinaten van A, afgerond op één decimaal, en teken het bijbehorende lijnstuk AB in de figuur hieronder.
     

 

 

       

 

Helderheid van sterren.
       
Aan de sterrenhemel bevinden zich heldere en minder heldere sterren. De helderheid van een ster werd in de oudheid reeds aangegeven met een getal, de magnitude van de ster. Zeer heldere sterren kregen magnitude 1. Nauwelijks zichtbare sterren kregen magnitude 6. Een kleine waarde betekent dus een grote helderheid. In deze opgave is m de magnitude.

Tegenwoordig meet men de hoeveelheid licht die van een ster wordt ontvangen. De helderheid van een ster wordt dan vaak uitgedrukt in lux (een eenheid voor verlichtingssterkte). In deze opgave is L de helderheid in lux.

In de tabel staan voor een aantal helderheden de waarden van m en L.
       
m 1,0 2,0 3,0 4,0 5,0 6,0
L 1,0 • 10-6 4,0 • 10-7 1,6 • 10-7 6,3 • 10-8 2,5 • 10-8 1,0 • 10-8
       
Tussen L en m bestaat een exponentieel verband van de vorm L = 10p + qm
       
4p. 4. Leid uit de tabelgegevens bij m = 1,0  en  m = 6,0  af dat  p = -5,6  en  q = -0,4
     

 

Voor L geldt dus:   L = 10-5,6 - 0,4m

In het sterrenbeeld Steenbok bevindt zich een optische dubbelster: twee sterren die met het blote oog als één object worden waargenomen. Na meting blijkt dat voor de ene ster geldt m = 4,30 en voor de andere ster m = 3,58. De waarde van L van de optische dubbelster is de som van de L-waarden van de afzonderlijke sterren.
       
4p. 5. Bereken de magnitude van de optische dubbelster. Rond je antwoord af op één decimaal.
     

 

L is omgekeerd evenredig met het kwadraat van de afstand x (in meters) van de ster tot de aarde:  L = C/x², waarbij C een constante is.

Er geldt het volgende verband:   m(x) = -14,0 - 2,5logC + 5,0logx
       
4p. 6. Bewijs dit.  
     

 

Momenteel is de afstand x van de ster Aldebaran tot de aarde 6,3 • 1017 meter. Deze afstand neemt toe met 1,7 • 1012 meter per jaar, dus  dx/dt =  1,7 • 1012  m/j.   Door deze verwijdering verandert ook de helderheid van de ster en dus ook de magnitude m.
De snelheid waarmee m verandert kan worden berekend met de afgeleide van m als functie van de tijd t (in jaren). Voor deze afgeleide dm/dt  geldt:

       
3p. 7. Bereken met behulp van differentiëren de snelheid waarmee de magnitude m van Aldebaran op dit moment verandert.
     

   
Gelijke hoeken.
       
Gegeven is cirkel c met middelpunt M. Op deze cirkel liggen de punten A en B zo, dat door A, B en M een cirkel d met middelpunt N gaat, waarbij N buiten c ligt.
Punt S ligt op cirkel d op de boog buiten cirkel c. Zie de volgende figuur.
       

       
Er geldt:  ∠ASM = ∠BSM
       
4p. 8. Bewijs dit.
     

 

De hierboven beschreven situatie geldt ook in onderstaande figuur. Punt S is nu zo gekozen dat lijnstuk AS door N gaat. Het snijpunt van AS en cirkel c is het punt C.
       

       
5p. 9. Bewijs dat ∠AMC = ∠ASB
     

   
Gelijke hellingen.
       
Voor elke a met -1/2π < a < 1/2π  wordt de functie  fa gegeven door  fa(x) = sinx • sin(x - a)  met domein [0, π].

De afgeleide van de functie fa  kan worden geschreven als  fa' (x) = sin(2x - a)
       
3p. 10. Bewijs dit.  
     

 

De functie g is gegeven door  g(x) = sinx  met domein  [0, π].

       

       
Deze twee grafieken raken elkaar in een punt met x = 2/3π. In dat punt is de helling van beide grafieken gelijk. Er zijn nog twee andere waarden van x waarvoor de helling van de grafiek van fπ/6 gelijk is aan de helling van de grafiek van g.
       
6p. 11. Bewijs dat deze x-waarden  2/3π van elkaar verschillen.
     

   

 

Hardheid.
       
De functie f wordt gegeven door  f(x) = √(25 - x2).
De grafiek van f  is een halve cirkel met middelpunt O(0, 0) en straal 5.

       
5p. 12. Bewijs dit.  
     

 

In onderstaande figuur is de grafiek van f getekend. We bekijken het deel van de grafiek tussen x = 5 - h  en  x = 5.
Door dit gedeelte te wentelen om de x-as ontstaat het bolsegment met dikte h. Zie de  figuur rechts.
       

       
Voor de grijs gemaakte oppervlakte A van het bolsegment, dus zonder de oppervlakte van de cirkelvormige linkerkant, geldt:

Met behulp van deze integraal kan exact worden berekend dat A = 10ph .
       
3p. 13. Bewijs dat  A = 10πh .
     

 

De formule A = 10πh  voor de oppervlakte van een bolsegment bewijst zijn nut bij de methode die de Zweed Brinell ontwikkelde voor het bepalen van de hardheid van materialen. Bij deze methode wordt gebruik gemaakt van een massieve bolvormige kogel die een diameter van 10 mm heeft. De kogel wordt met kracht tegen het te testen materiaal gedrukt, waardoor er in het materiaal een indruk in de vorm van een bolsegment ontstaat. De oppervlakte van dat bolsegment hangt af van de hardheid van het materiaal en de kracht waarmee wordt gedrukt.

Deze kracht mag niet zo groot zijn dat de kogel vervormt of voor meer dan de helft in het materiaal wordt gedrukt. In de praktijk wordt bij de hardheidsmeting volgens Brinell de diameter d (in mm) van de cirkelvormige rand van de indruk gemeten. In de volgende figuur is een dwarsdoorsnede getekend van een kogel met diameter 10 mm die een stukje in het materiaal is gedrukt. De diepte van de indruk is h (in mm).
       

       
Met behulp van deze figuur kan het volgende verband tussen h en d worden gevonden:

       
5p. 14. Bewijs de juistheid van deze formule.  
     

 

De hardheid volgens Brinell wordt aangeduid als HB. Deze hardheid wordt bepaald met de formule:  HB = 0,102 • F/A
Hierbij is F de kracht in newton (N) waarmee wordt gedrukt en A de oppervlakte van het bolsegment dat in het materiaal is gedrukt in mm2.

Bij een hardheidsmeting wordt de kogel met een kracht van 29400 N in het te testen materiaal gedrukt.
       
5p. 15. Bereken voor welke waarde van d de hardheid HB van het materiaal 340 is. Rond je antwoord af op één decimaal.
     

   

 

Raken aan een cirkel.
       
Gegeven zijn twee halve lijnen k en l vanuit punt A en een cirkel met middelpunt M die zowel k als l raakt. De raakpunten van k en l aan de cirkel zijn respectievelijk B en C. Zie de linker figuur. Uit de congruentie van driehoek ABM en driehoek ACM volgt dat AM bissectrice is van hoek BAC
       

       
In de rechter  figuur  is de situatie van de linker  figuur uitgebreid. Lijn m is evenwijdig aan k en raakt de cirkel in punt D. De lijnen l en m snijden elkaar in punt E. Uit de congruentie van driehoek ECM en driehoek EDM volgt dat EM bissectrice is van hoek CED.
       
6p. 16. Bewijs dat ∠AME = 90º  
     

 

In de  figuur hier onder zijn weer twee halve lijnen k en l vanuit punt A getekend. De hoek tussen k en l is scherp. Tussen deze halve lijnen ligt een punt F. Ook is de parabool getekend die brandpunt F en richtlijn k heeft. Door F kunnen twee cirkels worden getekend die zowel k als l raken. Een van deze cirkels is getekend.
       

       
4p. 17. Teken in de figuur het middelpunt N van de andere cirkel. Licht je werkwijze toe.
     

   

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
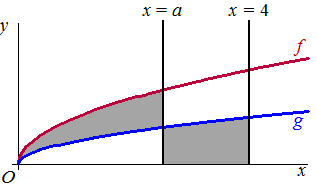
1. Snijpunt:  √x = 1/2√x  ⇒ 1/2√x = 0  ⇒ √x = 0  ⇒ x = 0
 

 

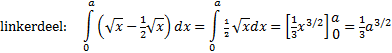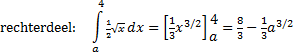  gelijkstellen:   1/3a3/2 = 8/3 - 1/3a3/2
2/3a3/2 = 8/3
a3/2 = 4
a = 42/3
   
2. B op  de x-as  ⇒  yB = 0  ⇒  2cos2t = 0  ⇒ cos2t = 0
2t = 1/2π + k2π  ∨  2t = -1/2π + k2π
t = 1/4 + kπ ∨  t =  -1/4π + kπ
Dat geeft de oplossingen  t = 1/4π, 3/4π, 5/4π,  7/4π
t = 1/4π  geeft   xA = 1/2√2  en  yA = 1/2√2
t =  3/4π geeft   xA = 1/2√2  en  yA = -1/2√2
t =  5/4π geeft   xA = -1/2√2  en  yA = -1/2√2
t =  7/4π geeft   xA = -1/2√2  en  yA = 1/2√2
Voor t = 1/4π  en  t = 5/4π  geldt   xA = yA dus ligt A op de lijn  y = x
Voor t = 3/4π  en  t = 7/4π  geldt   xA = -yA  dus ligt A op de lijn  y = -x
   
3. AB horizontaal:  yA = yB
Dat geeft  2cos(2t) = cost
Dit mag je natuurlijk met de GR (intersect) oplossen, maar we doen het natuurlijk liever algebraïsch:
2cos(2t) = cost
2(2cos2t - 1) = cost
4cos2t - cost - 2 = 0
ABC-formule:   cost =  (1 ± √(1 + 32))/8 = 1/8 ± 1/8√33
Onder de x-as is  cost negatief, dus  cost = 1/8 - 1/8√33  (≈ -0,593)
Dan is  xA = sint  =  ±√(1 - cos2t) =  ± 0,805
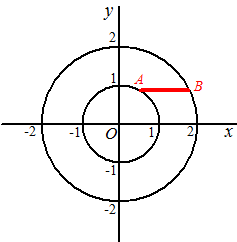
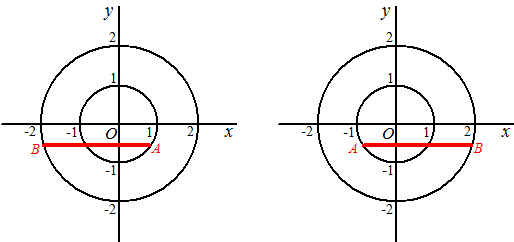
Dus  A = (0.8, -0.6)  of  A = (-0.8, -0.6)
De lijn y = -0,6 snijden met de cirkels geeft beide mogelijkheden hieronder.
   
 

   
4. m = 1  en  L = 10-6  invullen  geeft  10-6 = 10p + q   dus  p + q = -6
m = 6  en L = 10-8 invullen geeft  10-8 = 10p + 6q  dus  p + 6q = -8

Trek de vergelijkingen van elkaar af:   5q  = -2  dus  q  = -0,4
Invullen in  p + q = -6  geef dan  p =  -5,6     
   
5. m = 4,30  geeft  L = 10-5,6  - 0,4 · 4,3  = 10-7,32 
m = 3,58  geeft  L = 10-5,6 - 0,4 · 3,58  = 10-7,032
Voor de sterren samen is dan  L = 10-7,32 + 10-7,032 = 1,41· 10-7  
1,41 · 10-7   = 10-5,6 - 0,4m  
log(1,41 · 10-7) = -5,6 - 0,4m
-6,85 = -5,6 - 0,4m
-1,25 = -0,4m
m = 3,1
   
6.  L = 10-5,6m - 0,4 = C/x2
neem van beide kanten log:     log(10-5,6m - 0,4 ) =  log(C/x² )
-0,4m - 5,6 = log(C/x²)
-0,4m - 5,6 = logC - logx2
-0,4m - 5,6 = logC - 2logx
-0,4m = logC - 2logx + 5,6
m = (-1/0,4)logC + (2/0,4)logx - 5,6/0,4
m = -2,5logC + 5,0logx - 14,0
   
7. dm/dx = 5,0 • 1/(xln10)  = 5,0/(xln10)
voor x = 6,3 • 1017  is dan  dm/dx = 5,0/(6,3 • 1017 • ln10)

dx/dt =  1,7 • 1012 
dan is  dm/dt  = 1,7 • 1012   • 5,0/(6,3 • 1017 • ln10)  ≈ 5,9 • 10-6  per jaar
   
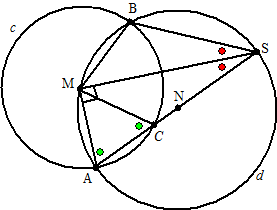
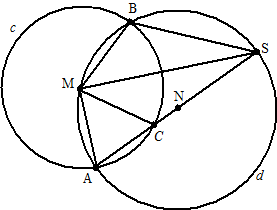
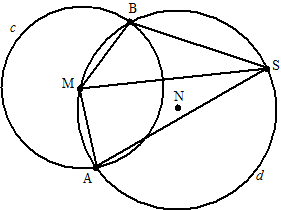
8. MA = MB (beiden straal van de linkercirkel)

Bij gelijke koorden horen gelijke omtrekshoeken.
∠ASM  is de omtrekshoek van AM
∠BSM is de omtrekshoek van BM

dus  ∠ASM = ∠BSM

   
9. ∠AMS = 90º  want AS is middellijn (Thales)
dus groen plus rood is 90º  (driehoek AMS)   ....(1)

De rode hoeken zijn gelijk (vraag 8)

De groene hoeken zijn gelijk (MAC is gelijkbenig, want MA = MC, dus zijn de basishoeken daarvan gelijk)

∠AMC = 180 - 2 • groen   (hoekensom AMC)
∠AMC = 180 - 2 • (90 - rood)    ....(1)
∠AMC = 2 • rood = ÐASB

   
10. fa(x) = sinx • sin(x - a)
met de productregel:
f ' =  cosx • sin(x - a) + sinx • cos(x - a)
Maar omdat  sin(α + β) = sinαsinβ + cosαcosβ  geldt hier: 
f ' = sin(x + x - a) = sin(2x - a)
   
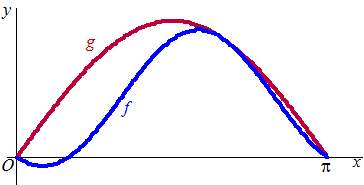
11. de hellingen gelijk, betekent  f ' = g'   dus in dit geval  sin(2x - 1/6π) = cosx
Maar cosx = sin(1/2π - x)
Dus  sin(2x - 1/6π) = sin(1/2π - x)
2x - 1/6π = 1/2π - x + k2π   of   2x - 1/6π = π - (1/2π - x) + k2π
3x = 2/3π + k2π   of   x = 2/3π + k2π
x = 2/9π + k2/3π   of  x = 2/3π + k2π

De eerste oplossing geeft twee waarden die 2/3π van elkaar verschillen vanwege de k • 2/3π
   
12.  f(x) = √(25 - x2) = (25 - x2)1/2 
met de kettingregel:  f '(x) =  1/2 • (25 - x2)-1/2 • -2x  =  x • (25 - x2)-1/2  
(f ' )2  = x2 • (25 - x2)-1  
 

   
13.


 
 
  = 5 • 5 - 5(5 - h) = 5h
Dus  A = 2π • 5h = 10πh
   
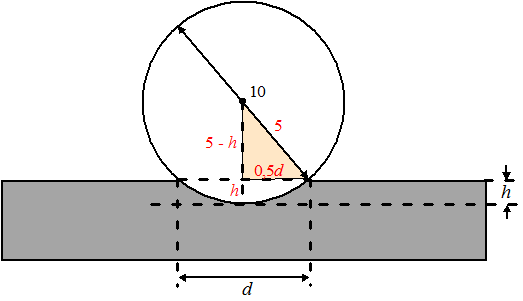
14.

   
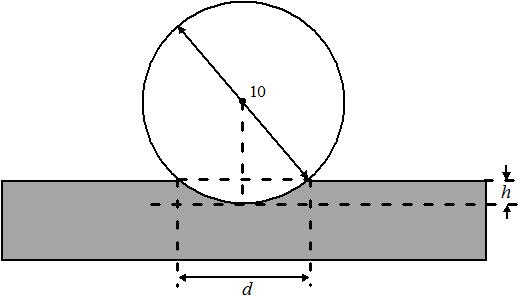
  Pythagoras in de gekleurde driehoek:   (5 - h)2 + (0,5d)2 = 52
(5 - h)2 = 25 - 0,25d2
4 • (5 - h)2 = 100 - d2
(5 - h)2 = (100 - d²)/4
 
 
   
15. 340 = 0,102 • 29400/A
29400/A = 340/0,102 = 3333,33...
A = 29400/3333,33... = 8,82

8,82 = 10πh 
h = 8,82/10π  = 0,2807...

0,2807 = (10 - √(100 - d²))/2
0,5614.. = 10 - √(100 - d2)
√(100 - d2) = 9,4385...
100 - d2 = 89,085...
d2 = 10,9146...
d ≈ 3,3 mm
   
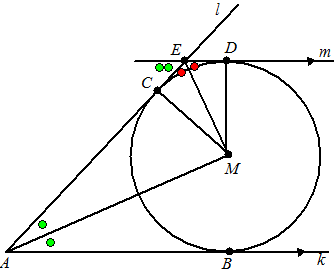
16. AM is de bissectrice dus de groene hoeken bij A zijn gelijk.
Vanwege Z-hoeken volgt daaruit de groene hoeken bij E

MC = MD (straal cirkel)
ME = ME
∠MDE = ∠MCE = 90º (raaklijn aan cirkel)
Dus de  MED is congruent met MEC (ZZR)

De rode hoeken bij E zijn dus gelijk.
Twee roden en twee groenen zijn 180º (gestrekte hoek bij E)
Dus rood  + groen  = 90º
Dan volgt uit driehoek AME dat ∠AME = 90º (hoekensom driehoek)

   
17. Het middelpunt van de cirkel moet op de parabool liggen, want heeft gelijke afstanden tot F en k  (beiden de straal van de cirkel)

Het middelpunt van de cirkel moet op de bissectrice van hoek A liggen, want heeft gelijke afstanden tot k en l  (raaklijnen).

Het middelpunt N is dus het snijpunt van de parabool met de bissectrice van hoek A.