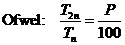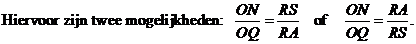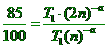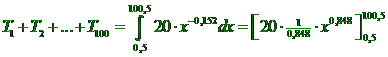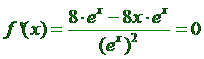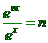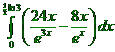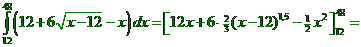VWO WB, 2010 - II
 

 

Snijden met een hoogtelijn.
     
Op een cirkel kiezen we drie vaste punten A, B en C, waarbij lijnstuk AB geen middellijn is en punt C op de kortste cirkelboog AB ligt.
Een punt P doorloopt dat deel van de langste cirkelboog AB waarvoor driehoek ABP niet stomphoekig is.
De hoogtelijn BQ van driehoek ABP snijdt de koorde CP in punt R. In onderstaande figuur is een mogelijke positie van P getekend met de bijbehorende punten Q en R.
       

       
Bij de beweging van P over het hierboven beschreven deel van de cirkelboog AB verandert de grootte van hoek BRC niet.
       
4p. 1. Bewijs dit.
     

 

De baan van R die hoort bij de hierboven beschreven beweging van P, kan getekend worden met behulp van de onder de figuur hierboven genoemde eigenschap.
     
5p. 2. Teken op deze manier in de figuur hierboven de baan van R. Geef de randpunten van de baan, waarbij driehoek ABP rechthoekig is, duidelijk aan. Licht je werkwijze toe.
     

 

De leercurve.
       
Het aanleren van een nieuwe handeling kost tijd. Als je een handeling vaker uitvoert, wordt de voor deze handeling benodigde tijd meestal steeds korter. T.P. Wright stelde voor dit leerproces de volgende formule op: Tn = T1 • n-a
Hierin is:
Tn het aantal seconden dat nodig is als de handeling voor de n-de keer wordt uitgevoerd,
T1 het aantal seconden dat nodig is als de handeling voor de eerste keer wordt uitgevoerd en
a een positieve constante die afhangt van de snelheid van het leerproces.

Volgens de formule van Wright leidt een verdubbeling van het aantal keer uitvoeren van een zelfde handeling tot een daling van de hoeveelheid benodigde tijd (en dus kosten) van de laatste keer met een vast percentage.
Men spreekt van een P%-leercurve als bij verdubbeling van het aantal keer uitvoeren van n naar 2n de laatste keer nog maar P% kost van de tijd bij de n-de keer.
       
4p. 3. Bereken de waarde van a in de formule van Wright bij een 85%-leercurve. Rond je antwoord af op twee decimalen.
     

 

In een bepaald bedrijf voeren mensen een handeling aan de lopende band uit. Deze handeling wordt niet door iedereen op dezelfde manier aangeleerd. In de praktijk komt men onder andere de volgende twee soorten mensen tegen:
− snelle starters: deze mensen kunnen de handeling de eerste keer al snel uitvoeren, maar het lukt hen daarna niet om dit snel te verbeteren,
− snelle leerders: de eerste keer duurt bij deze mensen wat langer, maar zij zijn in staat snel vooruitgang te boeken.
       
Voor beide soorten hanteert het bedrijf een formule van Wright:
− snelle starters: Tn = 20 • n-0,152
− snelle leerders: Tn = 40 • n-0,328
       
4p. 4. Bereken bij de hoeveelste keer uitvoeren een snelle leerder de handeling voor het eerst sneller uitvoert dan een snelle starter.
       
Men wil weten hoe lang een snelle starter bij de eerste 100 handelingen gemiddeld over een handeling doet. Daarvoor moet eerst de totale tijd, dus de som T1 + T2 + T3 + ... + T100 , uitgerekend worden. Deze som is gelijk aan de totale oppervlakte van 100 rechthoeken met breedte 1 en hoogtes T1, T2, T3, …, T100.
In de volgende figuur is een aantal van deze rechthoeken getekend voor een snelle starter.
       

       
De oppervlakte van de 100 rechthoeken kan goed benaderd worden met een oppervlakte onder de grafiek van de functie T die gegeven is door T(x) = 20 • x−0,152 .
       
4p. 5. Bereken deze oppervlakte onder de grafiek van T met behulp van primitiveren en bepaal hiermee hoe lang een snelle starter bij de eerste 100 handelingen gemiddeld over een handeling doet. Rond deze tijdsduur af op een geheel aantal seconden.
     

 

Een exponentiële functie.
       
In de onderstaande figuur is voor x ≥ 0 de grafiek getekend van de functie f die gegeven is door:   f (x) = 8x/ex
       

       
Deze grafiek heeft één top, die we A noemen.
       
4p. 6. Bereken exact de x-coördinaat van A.
     

 

       
Zoals je in de figuur hierboven  ziet, past een vierkant met zijde 1 waarvan één zijde op de x-as ligt, ruimschoots in het gebied tussen de grafiek van f en de x-as.
       
4p. 7. Onderzoek met een berekening of een vierkant met zijde 2 waarvan één zijde op de x-as ligt, ook nog in dit gebied past.
     

 

We bekijken nu voor positieve waarden van n met n ≠1 de functie gn die is gegeven door  gn(x) = 8nx/ex

De grafieken van gn snijden de grafiek van f in het punt (0, 0). Ook is er voor elke positieve waarde van n met n ≠ 1 nog een ander snijpunt.
In de volgende tabel staat voor enkele waarden van n de x-coördinaat van dit andere snijpunt.
       
n 2 3 4 5
xsnijpunt ln2 1/2ln3 1/3ln4 1/4ln5
       
Voor de vier waarden van n uit de tabel geldt:   xsnijpunt = 1/(n-1) • ln n
Hieruit ontstaat het vermoeden dat deze formule voor snijpunt x klopt voor elke positieve waarde van n met n ≠1.
       
5p. 8. Toon aan dat dit vermoeden juist is.
     

 

       
In de bovenstaande figuur zijn de grafieken getekend van f en de functie g3, gegeven  door  g3(x) = 24x/e3x
De grafieken van f en g3 sluiten een vlakdeel in. Dit vlakdeel is in de figuur grijs gemaakt.
       
4p. 9. Bereken de oppervlakte van dit vlakdeel.
     

 

Wortelfuncties.
       
In de volgende figuur is de grafiek van f12 getekend en de lijn met vergelijking y = x.
       

 
8p. 10. Bereken exact de oppervlakte van het vlakdeel dat wordt ingesloten door de lijn met vergelijking y = x en de grafiek van f12 .
     

 

Verder is gegeven de lijn k met vergelijking y = x + 9
       
6p. 11. Bewijs dat voor elke waarde van n de grafiek van fn de lijn k raakt in het punt met x-coördinaat n + 9 .
     

 

 

Zoek de geodriehoek.
       
Gegeven zijn twee evenwijdige lijnen k en m en een punt A ertussenin. Zie de figuur.
       

       
In deze opgave bekijken we hoe je op elk van de twee gegeven lijnen een punt kunt tekenen zo dat deze punten samen met punt A de hoekpunten zijn van een geodriehoek. Een geodriehoek is een gelijkbenige rechthoekige driehoek. We bekijken de situatie waarbij de hoek waarvan A het hoekpunt is, recht is.

Om te begrijpen hoe we die situatie kunnen tekenen, bekijken we onderstaande figuur. Hierin is een geodriehoek PQR getekend, waarbij hoek P recht is en de punten Q en R respectievelijk op de (evenwijdige) lijnen k en m liggen. De loodlijn door P op k en m snijdt k in punt S en m in punt T.
       

       
Er geldt: driehoek PQS is congruent met driehoek RPT.
       
4p. 12. Bewijs dit.
     

 

In de figuur hieronder zijn twee evenwijdige lijnen k en m getekend met een punt A ertussenin.
       

       
3p. 13. Teken in deze figuur met behulp van wat hierboven  gezegd is een geodriehoek waarvan op elk van deze lijnen k en m een hoekpunt ligt en waarvan A het hoekpunt van de rechte hoek is. Licht je werkwijze toe.
     

 

Gebroken functie.
       
Voor elke positieve waarde van a is de functie fa gegeven door  fa(x) = ax + 1/x met x > 0
In de volgende figuur is voor enkele waarden van a de grafiek van fa getekend.
       
       
De grafiek van fa heeft voor elke positieve waarde van a een top. Het lijkt erop dat deze toppen liggen op een hyperbool met vergelijking xy = c voor een zekere waarde van c. Deze hyperbool is in de figuur gestippeld weergegeven.
       
5p. 14. Toon langs algebraïsche weg aan dat de toppen inderdaad op een hyperbool met vergelijking xy = c liggen en bereken de waarde van c.
     

 

Rechthoeken bij een kwartcirkel.
       
In een rechthoekig assenstelsel Oxy bekijken we het deel van de eenheidscirkel dat in het eerste kwadrant ligt. Het snijpunt met de x-as is A(1, 0). Op de kwartcirkel ligt een willekeurig punt B(cost, sint) met ∠AOB = t rad en  0 < t < 1/2π .
Punt R is de loodrechte projectie van B op de x-as.
We maken nu twee rechthoeken:
       
  I.  Een rechthoek ONPQ, waarbij N het midden van AR is en P en Q op dezelfde hoogte als B liggen.
OQ = sint en  ON = 1/2(1 + cos t) .
Zie de figuur hieronder.
De oppervlakte van deze rechthoek noemen we V(t) .		   II.  Een rechthoek ATSR, waarbij S
het midden van BR is.
RS = 1/2sint en RA = 1 − cost .
Zie de figuur hieronder.
De oppervlakte van deze rechthoek noemen we W(t) .
       
 

 
       
5p. 15. Bereken exact de waarde van t waarvoor V(t) = 3 •W(t) .
     

 

De bovengenoemde rechthoeken zijn gelijkvormig als de verhouding van de zijden van de ene rechthoek gelijk is aan de verhouding van de zijden van de andere rechthoek.
       
4p. 16. Toon aan dat voor elke waarde van t met 0 < t < 1/2π geldt:  ON/OQ = RS/RA
     

 

Er is een waarde van t (met 0 < t < 1/2π ) waarvoor geldt dat   ON/OQ = RA/RS
Voor deze waarde van t zijn beide rechthoeken vierkant.
       
7p. 17. Bereken van beide vierkanten exact de zijde voor deze waarde van t.
     

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
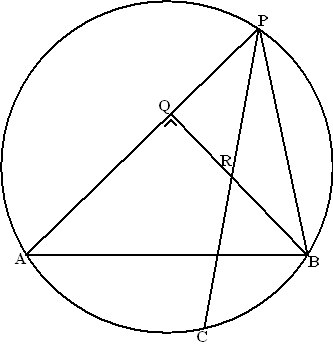
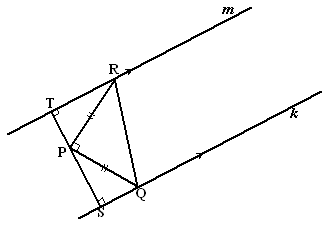
1. ∠APC is constant (omtrekshoek van AC)
Dus is ∠QRP constant (hoekensom driehoek QRP)
Dus is ∠CRB constant (overstaande hoeken)
   
2. Omdat ∠BRC constant is liggen B, C en alle punten R op één cirkel.
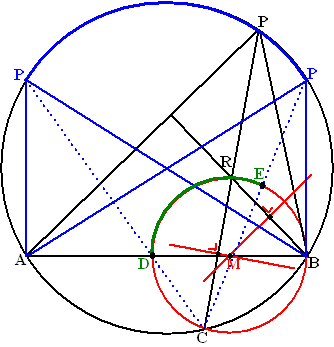
Teken de middelloodlijn van RC en die van BR. Waar deze twee middelloodlijnen elkaar snijden ligt het middelpunt van de gezochte cirkel.

Die cirkel kun je dan tekenen (rode cirkel hiernaast)

ABP mag geen stompe hoek hebben.
Teken de grensgevallen AP en BP waarbij de driehoek ABP rechthoekig is (blauw hiernaast).

Verbind C met beide punten P, en je snijdt een stuk van de rode cirkel af waar R op moet liggen.
(het groene deel hiernaast)

 
   
3.
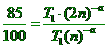  T1 valt weg.
Kruislings vermenigvuldigen geeft  0,85 • n-a = (2n)-a
0,85n-a = 2-a • n-a
2-a = 0,85
-a = 2log(0,85)
a = - 2log(0,85)  ≈ 0,23
   
4. 40 • n-0,328 = 20 • n-0,152
Voer inde GR in  Y1 = 40 * X^-0,328  en  Y2 = 20 * X^-0,152
Kijk in TABLE waar Y1 voor het eerst kleiner is dan Y2
Dat is bij n = 52
   
5.
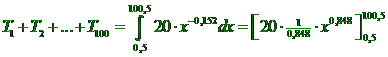  = (20 • 1/0,848 • 100,50,848 - 20 • 1/0,848 • 0,50,848) = 1163
Dus de gemiddelde tijd is 1163/100 ≈ 12 seconden.
   
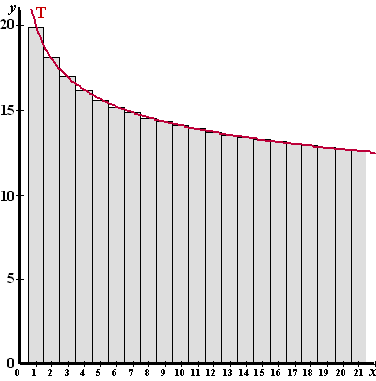
6. Voor de top geldt  f '(x) = 0.
Met de quotiëntregel:
 
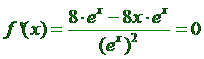  Een breuk is nul als de teller nul is:  8ex - 8x • ex = 0 ⇒ 8ex (1 - x) = 0 ⇒ x = 1
   
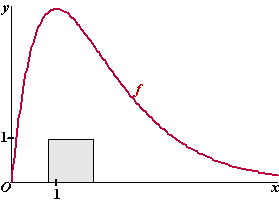
7. De bovenrand van het vierkant bevindt zich op de lijn y = 2.
Bereken de snijpunten van y = 2 met de grafiek:  2 = 8x/ex
Y1 = 2  en  Y2 = 8X/(e ^X)  en dan intersect geeft x = 0,4 en x = 2,2
De afstand daartussen is minder dan 2, dus het vierkant past niet.
   
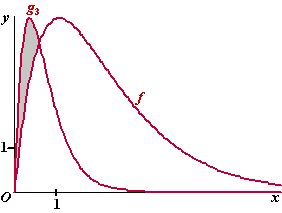
8. Snijden:  8x/ex = 8nx/enx 
Kruislings vermenigvuldigen:  enx • 8x = ex • 8nx
enx • 8x - ex • 8nx = 0
8x(enx - nex) = 0
enx = nex
 
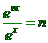  e(n - 1)x = n
(n - 1)x = lnn
x = 1/(n - 1) • lnn
   
9. Het snijpunt van beide grafieken ligt bij x = 1/2ln3  (zie boven vraag 8)
 
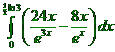  Voer in de GR in:  Y1 = 24X/(e^(3X)) - 8X/(e^X)  en gebruik  calc - 7  met ondergrens 0, bovengrens 0,5ln3
Dat geeft oppervlakte 0,46.
   
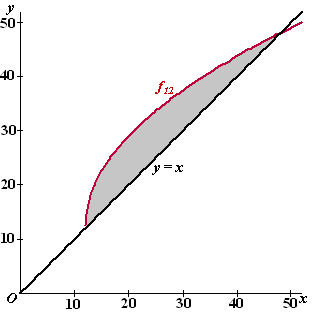
10. Snijpunt:  12 + 6√(x - 12) = x
6√(x - 12) = x - 12
kwadrateren:  36(x - 12) = (x - 12)2 = x2 - 24x + 144
36x - 432 = x2 - 24x + 144
x2 - 60x + 576 = 0
de ABC formule geeft  x = 48 of x = 12
 
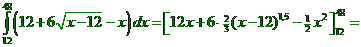  (12 • 48 + 4(48 - 12)1,5 - 0,5 • 482) - (12 • 12 + 4(12 - 12)1,5 - 0,5 • 122) = 216.
   
11. Als twee grafieken elkaar raken in punt R, dan moeten ze beiden door R gaan, en dan moeten ze in R dezelfde helling hebben.

x = n + 9 geeft  y = n + 6√(n + 9 - n) = n + 6 • √9 = n + 6 • 3 = n + 18  = x + 9
Dus het punt  (n + 9, n + 18) ligt inderdaad op beide grafieken.

De helling van  y = x + 9 is gelijk aan 1.

De helling van y = n + 6√(x - n)  is de afgeleide:  y' = 6 • 0,5 • (x - n)-0,5
x = n + 9 geeft dan   y' = 6 • 0,5 • (n + 9 - n)-0,5 = 3 • 9-0,5 = 3 • 1/3 = 1

De grafieken hebben in het punt (n + 9, n + 18) beiden helling 1, dus raken ze elkaar daar.
 
   
12. ∠SPQ + ∠SQP = 90º  (samen met de rechte hoek QPR zijn het de hoeken van een driehoek)
∠SPQ + ∠TPR = 90º  (samen met de rechte hoek QPR vormen ze een gestrekte hoek)
Dus ∠SQP = ∠TPR
∠PSQ = ∠PTR (= 90º)
PR = PQ
Dus zijn de driehoekencongruent (ZHH)
   
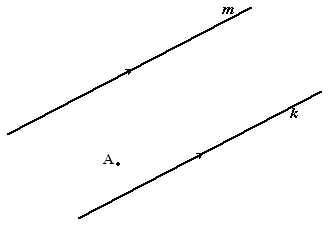
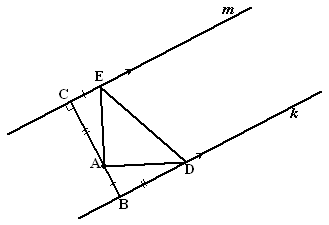
13. Teken een lijn door punt A loodrecht op k en m. Noem de snijpunten met k en m respectievelijk  B en C
Teken nu E en D zó dat  CE = AB  en  BD = AC (zie de figuur hiernaast)
Dan zijn de driehoeken ACE en ABD congruent en is de driehoek een geodriehoek.

   
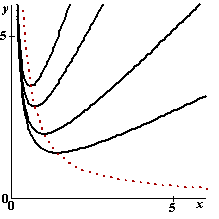
14. In de top is de afgeleide nul:  f ' = a - x-2 = 0
Dan is  x-2 = a ⇒   1/x2 = a   ⇒   x2 = 1/a   ⇒ x = √(1/a)   (de negatieve oplossing voldoet niet)
 
  x • y = √(1/a) • 2√a =  2√(1/a • a) = 2
Dat is inderdaad constant, dus c = 2
   
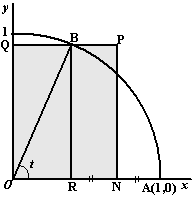
15. De oppervlakte is lengte keer breedte:
V(t) = 1/2sint • (1 + cost)  en  W(t) = 1/2sint • (1 - cost)
V = 3 • W  ⇒  1/2sint • (1 + cost) = 3 • 1/2sint • (1 - cost)
1 + cost = 3(1 - cost)     (of sin1/2t = 0, maar dat geeft t = 0 en die voldoet niet)
1 + cost = 3 - 3cost
4cost = 2
cost = 1/2
t = 1/3p.
   
16. De vergelijkingen invullen:
 
  kruislings vermenigvuldigen:  1/2(1 + cost)(1 - cost) = 1/2sin2t
(1 + cost)(1 - cost) = sin2t
1 - cost + cost - cos2t = sin2t
1 - cos2t = sin2t
sin2t + cos2t = 1
Dat is inderdaad zo.
   
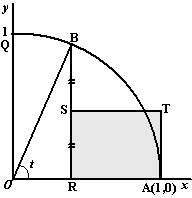
17. Als ATSR vierkant is dan geldt  1/2sint = 1 - cost
kwadrateren:  1/4sin2t =  (1 - cost)2
1/4(1 - cos2t) = 1 - 2cost + cos2t
1/4 - 1/4cos2t = 1 - 2cost + cos2t
11/4cos2t - 2cost + 3/4 = 0
5cos2t - 8cost + 3 = 0
De ABC formule geeft dan  cost = 3/5  (of cost = 1 maar die voldoet niet)
Als cost = 3/5  dan is  RA = 1 - 3/5 = 2/5  en   ON = 1/2(1 + 3/5) = 4/5

(Als ONPQ vierkant is dan krijg je sint = 1/2(1 + cost) en die kun je op precies dezelfde manier oplossen)