VWO WB12, 2008 - II
Een zwaartepunt.

Van een cirkelschijf met middelpunt (0, 0) en straal 1 is het kwart getekend dat in het eerste kwadrant ligt. De cirkelboog is de grafiek van de functie f die gegeven is door f (x) = 1− x2 op het domein [0, 1]. Zie de bovenste figuur hiernaast.

We wentelen het kwart van de cirkelschijf om de x-as. Het omwentelingslichaam dat dan ontstaat is een halve bol. Zie de onderste figuur hiernaast.

Het zwaartepunt van de halve bol ligt op de positieve x-as

Voor de x-coördinaat xZ  van dit zwaartepunt geldt:

xZ = M/V ,  met

V is de inhoud van de halve bol.

De inhoud van een bol met straal r is gelijk aan 4/3πr3 .

     
6p. 1. Bereken x2 exact.

 

 

Onder een grafiek.

De functie f is gegeven door f (x) = e-x² . Het punt P(p, e-p² ) ligt op de grafiek van f, waarbij p > 0 .
Onder de grafiek van f  ligt een rechthoek PQRS met P en Q op de grafiek en R en S op de x-as. Dus S is het punt ( p, 0 ). Zie de volgende figuur.

Punt P kan zo op de grafiek van f gekozen worden dat PQ = PS.  PQRS is dan een vierkant.
4p. 2. Bereken de oppervlakte van dit vierkant.

 
Er is een waarde van p waarvoor de oppervlakte van PQRS maximaal is.
5p. 3. Bereken deze waarde van p exact.

 
Een dobbelspel.

De personen K en L spelen een dobbelspel. Elk van de spelers begint met twee fiches; de pot is dan nog leeg. Bij het spel wordt geworpen met speciale dobbelstenen: op vier kanten van zo'n dobbelsteen staat een stip (•), op één kant een A en op één kant een P.  Zie figuur.

De spelregels zijn:
- De spelers werpen om de beurt met één of twee dobbelstenen.
- De speler die aan de beurt is, werpt met één dobbelsteen als hij één fiche heeft en met twee dobbelstenen als hij twee of meer fiches heeft.
- Voor elke A die een speler werpt, moet hij 1 fiche aan de andere speler geven.
- Voor elke P die een speler werpt, moet hij 1 fiche in de pot doen.
- Voor een stip (•) hoeft hij geen fiche af te geven.
- Wanneer een speler geen fiches meer heeft, heeft hij verloren (en de andere speler gewonnen).

Hiernaast staat een mogelijk spelverloop waarbij speler K is begonnen. In zijn tweede beurt werpt speler K met één dobbelsteen want hij heeft nog maar één fiche.

Neem aan dat speler K begint.

De kans dat speler K na zijn eerste beurt nog 1 fiche heeft en L dan 3 fiches heeft, is 2/9.

3p. 4. Toon dit aan.

 

Op een gegeven moment heeft K 2 fiches, L 1 fiche en de pot 1 fiche. Op dit moment is L aan de beurt.
4p. 5.

Bereken de kans dat, na deze beurt van L, K nog één beurt krijgt en het spel daarna afgelopen is.

 

Een toeschouwer heeft het spel met de computer heel vaak gesimuleerd. Op grond van het resultaat beweert hij dat de speler die begint, 43% kans heeft om het spel te winnen en de andere speler 57%.
De spelers K en L spelen het spel tien keer, waarbij speler K steeds begint. Veronderstel dat de toeschouwer gelijk heeft.
6p. 6. Bereken de kans dat een van beide spelers minstens zeven keer wint.

 

 

Driehoek en cirkel.

In onderstaande figuur is een scherphoekige driehoek ABC getekend, met AC > AB, en de cirkel met middelpunt A en straal AB. Deze cirkel snijdt BC in D en AC in E. De grootte van ∠BAC noemen we α.

5p. 7. Druk ∠CDE uit in α. Bewijs dat je antwoord juist is.

 
Dozen met vaste inhoud.

Uit een lange strook karton met een breedte van 15,0 dm worden dozen gemaakt met vierkante bodem en deksel en rechthoekige zijkanten. Daartoe wordt het karton verknipt in rechthoeken waarvan de breedte gelijk is aan 15,0 dm en de lengte afhangt van de gewenste hoogte van de doos. We noemen de hoogte van de doos in dm x.
Zo’n rechthoekig stuk karton wordt op acht plaatsen x dm ingeknipt, waarna zes vierkantjes van x bij x dm worden omgevouwen. Zie figuur 9. De stippellijnen zijn vouwlijnen. Tot slot wordt het karton gevouwen tot een doos. Zie de figuur hieronder.

De inhoud van de doos moet 100 dm3 zijn.
6p. 8.

Bereken bij welke lengtes van de kartonnen rechthoek dit het geval is. Geef je antwoord in dm, afgerond op 1 decimaal.

 

Er zijn ook stroken karton te verkrijgen met een andere breedte dan 15,0 dm. De breedte van het stuk karton in dm noemen we b. Zie de volgende figuur.

We kijken in het vervolg van deze opgave steeds naar dozen waarvoor geldt:
− de bodem en het deksel zijn vierkant,
− de vier zijvlakken zijn rechthoekig,
− de inhoud is 100 dm3.

Er geldt:  (b - 2x)2 = 100/x
3p. 9. Toon aan dat deze formule juist is.

 

Uit deze formule volgt dat  b = 2x + 10/√x

De oppervlakte A van de kartonnen rechthoek waaruit de doos gemaakt wordt, is afhankelijk van x.

Er geldt: A = 6x2 + 70√x + 200/x
5p. 10. Toon aan dat deze formule juist is.

 

Er zijn twee dozen (doos 1 en doos 2) die aan de specificaties voldoen en waarvoor geldt:
-

doos 2 is vier keer zo hoog als doos 1 (dus voor de hoogtes x1 en x2 van doos 1 en doos 2 geldt x2 = 4 • x1) en
-

voor doos 1 en doos 2 is evenveel karton nodig (dus voor de benodigde oppervlaktes A1 en A2 van de kartonnen rechthoeken waaruit doos 1 en doos 2 gemaakt worden, geldt A2 = A1).
     
4p. 11. Bereken x1. Geef je antwoord in dm, afgerond op 2 decimalen.

 

 

Zee verdelen.

Een zee wordt begrensd door twee rechte kustlijnen: aan de ene kustlijn ligt land A, aan de andere land B. G is het gemeenschappelijke punt van de kustlijnen. In de zee ligt een ministaatje C dat we benaderen door een punt. Zie de volgende figuur.

De zee wordt verdeeld tussen A, B en C volgens het naaste-buurprincipe.
6p. 12.

Teken in de figuur de grenzen bij deze verdeling. Licht je tekening toe.

 

In de figuur hieronder is een drielandenpunt D getekend. Er geldt dus: DK = DL = DC. In deze figuur zijn de raaklijnen aan twee aanliggende stukjes grenslijn in D getekend. De grootte van de hoek tussen de twee raaklijnen noemen we β. De grootte van de hoek die de rechte kustlijnen met elkaar maken in G noemen we α.

4p. 13. Toon aan dat  β = 90º - 1/2α

 

 

Exponentiële rijen

Een rij u0, u1, u2, ... is gegeven door:

met a > 1.
In onderstaande figuur zijn voor een zekere waarde van a in een rechthoekig assenstelsel Oxy de grafiek
van y = ax en de lijn y = x getekend.

3p. 14.

Teken met behulp van een webgrafiek in de figuur op de uitwerkbijlage de plaats van u1 en u2 op de x-as.

In de situatie hierboven convergeert de rij u0 , u1, u2 , …. In onderstaande figuur zijn voor een andere waarde van a de grafiek van y = ax en de lijn  y = x getekend. In deze situatie convergeert de rij u0 , u1, u2 , … niet.

6p. 15.

Bereken exact de grootste waarde van a waarvoor de rij u0 , u1, u2 , … convergeert.

 
Rechthoek in ovaal.

Het ovaal in onderstaande figuur bestaat uit een vierkant van 2 bij 2 met aan weerszijden een halve cirkel met straal 1. M is het middelpunt van een van de halve cirkels.

In het ovaal wordt een rechthoek ABCD getekend met de hoekpunten op de halve cirkels en met de zijden evenwijdig aan de zijden van het vierkant.  ∠MAB = α rad (0 < α < 1/2π). Zie volgende figuur. Hierin is de rechthoekige driehoek AMS te zien met rechthoekszijden sinα en cosα .

De oppervlakte O van rechthoek ABCD kan uitgedrukt worden in α. Er geldt: O = 2sin 2α + 4sin α.
4p. 16. Toon aan dat deze formule juist is.

 
Er geldt:  dO/dα = 8 • cos 11/2α • cos 1/2α.
4p. 17.

Toon aan dat de formule voor  dO/dα  juist is.

 

Er is een waarde van α, met 0 < α < 1/2π, waarvoor de oppervlakte van rechthoek ABCD maximaal is.
4p. 18.

Bereken langs algebraïsche weg de maximale oppervlakte van rechthoek ABCD.

 

 

UITWERKING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. V = 1/2 • 4/3 • π • 13 = 2/3π.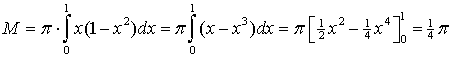

xZ = M/V = 3/8
2. PQ  = PS geeft  2p = e-p²
Y1 = 2X en  Y2 = e^(-X^2) en dan intersect geeft  p ≈ 0,41936
De oppervlakte is dan p2 ≈ 0,176
3. De oppervlakte is gelijk aan O = PQ • PS = 2p • e-p² 
Bij het maximum moet de afgeleide nul zijn.
Met de productregel en de kettingregel:
O' = 2 • e-p² +  2p • e-p² • -2p  = 2e-p² • (1 - 2p2)
O'= 0  ⇒  1 - 2p2 = 0   ⇒   p2 = 1/2  ⇒  p = ±√(1/2) = ±1/2√2
Omdat p > 0 moet gelden p = 1/2√2.
Het bewijs dat het inderdaad om een maximum gaat volgt uit het tekenbeeld van O',
(0)+++++(1/2Ö2)--------
4. Om dat te laten gebeuren moet K een stip en een A gooien.
P(•A) + P(A•) = 4/6 • 1/6 + 1/6 • 4/6 = 4/36 + 4/36 = 8/36 = 2/9.
5. Dan moet eerst L zijn fiche niet kwijt raken, en daarna K zijn beide fiches wél.
P(L raakt zijn fiche niet kwijt) = 4/6
P(K raakt beide fiches kwijt) = 2/6 • 2/6 = 4/36
De totale kans wordt dan  4/6 • 4/36 = 2/27
6. Dit is een binomiaal experiment met n = 10 en p = 0,57 of 0,43
P(K wint minstens 7 keer) = P(X ≥ 7) = 1 - P(X ≤ 6) = 1 - binomcdf(10, 0.43, 6) = 0,0806
P(L wint minstens 7 keer) = P(X ≥ 7) = 1 - P(X ≤ 6) = 1 - binomcdf(10, 0.57, 6) = 0,3102
P(één van beiden wint minstens 7 keer) = 0,0806 + 0,3102 = 0,3908
7. Noem ∠ABD = ∠ADB = β   (gelijkbenige driehoek)
Noem ∠AED = ∠ADE = γ    (gelijkbenige driehoek)
Dan is  α = (180 - 2β) + (180 - 2γ) = 360 - 2β - 2γ   (hoekensom driehoek ABD)
 ∠CDE = 180 - β - γ   (gestrekte hoek) 
Uit de laatste twee regels volgt   ∠CDE =  1/2α.  

of:
de omtrekshoek van BE is 360 - α.
dan is de middelpuntshoek 180 - 1/2α, maar dat is ∠BDE
dan is de gevraagde hoek 1/2α (samen een gestrekte hoek)
8. Stel de lengte L
De hoogte van de doos is x, de breedte van de doos is 15 - 2x en de breedte ook (de doos is vierkant)
De inhoud is dus  x • (15 - 2x) • (15 - 2x) = 100
Y1 = x • (15 - 2x) • (15 - 2x)  en  Y2 = 100  en dan intersect levert x = 0,512  of  x = 5,335
Lengte L = (15 - 2x) + (15 - 2x) + 3x = 30 - x  = 29,5 dm of 24,7 dm
9. De breedte van de bodem is  b - 2x
De inhoud is dan  (b - 2x)2 • x en dat moet gelijk zijn aan 100
(b - 2x)2 • x = 100  ⇒  (b - 2x)2 = 100/x
10. bodem + deksel hebben zijde b - 2x = 10/√x
De rechthoek heeft dus lengte 3x + 2 • 10/√x = 3x + 20/√x
de oppervlakte is dan  (3x + 20/√x) • (2x + 10/√x)
dat is  6x2 + 30x/√x + 40x/√x + 200/x = 6x2 + 30√x + 40√x + 200/x = 6x2 + 70√x + 200/x
11. Neem  x = x1
A1 = 6x2 + 70√x + 200/x  en   A2 = 6(4x)2 + 70√(4x) + 200/(4x)
Die moeten gelijk zijn:   6x2 + 70√x + 200/x =  6(4x)2 + 70√(4x) + 200/(4x)
Invoeren bij Y1 en Y2 en dan intersect geeft  x ≈ 0,97 dm.
12. de conflictlijn van een punt met een lijn is een parabool, dus de conflictlijnen tussen C en A en C en B zullen twee parabolen zijn.
De conflictlijn tussen twee snijdende lijnen is de bissectrice daarvan, dus de conflictlijn tussen A en B zal de bissectrice zijn. Die zijn allemaal in de linkerfiguur hieronder getekend.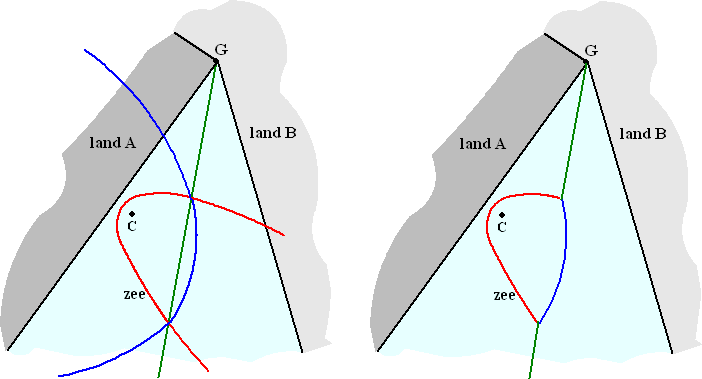



Daaruit volgen de grenzen van de rechterfiguur.
13. De raaklijnen zijn raaklijnen aan parabolen en dat zijn de bissectrices van de hoeken (raaklijneigenschap parabool) Dus ∠β = 1/2 ∠KDL
Maar KDLG is een vierhoek met hoekensom 360º, en omdat twee hoeken ervan 90º zijn moeten de twee anderen samen 180º zijn, dus ∠KDL + α = 180  ⇒  ∠KDL = 180 - α
 ∠β = 1/2∠KDL = 1/2(180 - α) = 90 - 1/2α.
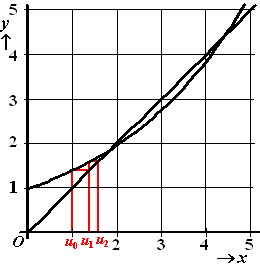
14. Ga steeds naar de grafiek van ax en dan weer naar de lijn y = x zoals hiernaast.
Dat levert op de x-as de gezochte u-waarden.
15. Het grensgeval zal zijn als de twee grafieken y = x  en  y = ax  elkaar raken.
Dan zijn hun hellingen gelijk:  1 = ax • lna
Verder gaan ze door het zelfde punt:  x = ax
Deze invullen in de regel erboven geeft  1 = x • lna  ofwel  lna = 1/x  dus  a = e1/x
x = ax  geeft dat  x = (e1/x)x = e  en dan is a = e1/e
16. De twee zijstukken hebben elk oppervlakte  cosa • 2sina = sin2a dus samen 2sin2a
het middenstuk heeft oppervlakte 2 • 2sina = 4sina
Samen geeft dat de gezochte formule.
17. met de kettingregel:  dO/da = 2cos2a • 2 + 4cosa = 4cos2a + 4cosa = 4(cos2a + cosa)
gebruik de formule voor cosa + cosb van de formulekaart met a = 2a en b = a
dat geeft  4 • (2cos1/2(2a + a) cos1/2(2a - a)) = 8cos11/2acos1/2a
18. dO/dα = 0  Þ  cos11/2α = 0  ∨  cos1/2α = 0
 ⇒  11/2α = 1/2π  ∨  11/2α = 11/2π  ∨  1/2α = 1/2π  ∨  1/2α = 11/2π
 ⇒  α = 1/3π  ∨  α = π  ∨  α = π  ∨  α = 3π
Omdat 0 < α < 1/2π zal de oplossing moeten zijn α = 1/3π.
Een tekenbeeld van dO/dα is       (0)++++(1/3π)-----(1/2π)     dus O heeft inderdaad een maximum
O(1/3π) = 2 • sin (2/3π) + 4sin(1/3π) = 2 • 1/2√3 + 4 • 1/2√3 = 3√3