Nieuwe pagina 1

Podiumverlichting

Een podium is 6 meter diep. Midden boven het podium hangt een balk met tl-buizen. De verlichtingssterkte op het podium is het kleinst aan de rand, bijvoorbeeld in punt P. De afstand van P tot de balk is r meter, de hoogte van de balk boven het podium is x meter en de hoek die het kortste verbindingslijnstuk van de balk en punt P met het podium maakt is a radialen. Zie de volgende figuur.

De verlichtingssterkte op het podium in punt P noemen we V (in lux). V is omgekeerd evenredig met r en evenredig met sina. Dus V = c • ¹/_r • sinα, waarbij de evenredigheidsconstante c afhangt van het lichtvermogen van de tl-buizen.
Voor deze balk met tl-buizen geldt: c = 650 (lux • m)
Er geldt:

Toon aan dat deze formule juist is.

De balk met tl-buizen kan omhoog gehesen worden: de hoogte kan variëren van 2,0 tot 5,0 meter.

De verlichtingssterkte op het podium in punt P moet minimaal 100 lux zijn.

Bereken langs algebraïsche weg op welke hoogtes de balk mag hangen.

Er is een hoogte van de balk waarbij V maximaal is.

Bereken deze hoogte langs algebraïsche weg.

Krasbal.

In 2001 werd het spel 'krasbal' geïntroduceerd. Het spel werd op één speelkaart door twee spelers gespeeld. In deze opgave is de speelkaart ("krasbalkaart") sterk vereenvoudigd. Hiernaast zie je de krasbalkaart, bestaande uit het "speelveld" en het "scoringsveld". In het speelveld zijn acht vakjes die kunnen worden open gekrast: vier met de letter V (van balVerlies) en vier met de letter P (van doelPoging). In het scoringsveld zijn vier vakjes die kunnen worden open gekrast: twee met de letter D (van Doelpunt) en twee met de letter M (van Misser)

4p	4.	Hoeveel verschillende krasbalkaarten zijn er mogelijk?

Het spel wordt als volgt gespeeld:
-	als een speler aan de beurt is, krast hij eerst een vakje in het speelveld open:
-	als hij in het speelveld:
	•	een V open krast, gaat de beurt naar zijn tegenstander
	•	een P open krast, gaat hij verder naar het scoringsveld;
-	als hij in het scoringsveld:
	•	een D open krast, heeft hij de wedstrijd gewonnen en stopt het spel.
	•	een M open krast, gaat de beurt naar zijn tegenstander.

Het aantal hokjes dat in een wedstrijd wordt open gekrast, is de lengte van een wedstrijd.

4p	5.	Bereken de kans dat een wedstrijd lengte 4 heeft.

Ruud en Patrick spelen het krasbalspel vaak. Het valt Patrick op dat, als Ruud mag beginnen, hij bijna altijd een P open krast. Het lijkt wel alsof Ruud kan zien wat er in een vakje staat! Patrick gaat in de komende tien spellen die Ruud mag beginnen, bijhouden hoe vaak het eerste vakje dat Ruud open krast een P is. Als dit er acht of meer zijn, zal hij Ruud van vals spel beschuldigen.

4p	6.	Bereken de kans dat hij Ruud ten onrechte van vals spel zal beschuldigen.

Cirkelinham

Een gebied G heeft aan een van zijn rechte zijden, EF, een inham, waarvan de rand bestaat uit drie cirkelbogen:

boog AB is een kwartcirkel met straal 3 en middelpunt E

boog CD is een kwartcirkel met straal 3 en middelpunt F

boog BC is een halve cirkel met straal 6 en middelpunt M

E, A, D en F liggen op een rechte lijn.

Zie de volgende figuur.

In de figuur hieronder zijn in de inham de iso-afstandslijnen getekend op de afstanden 1, 2, 3 en 4 van het land.

Teken in de bovenste figuur de iso-afstandslijn waarop punt M ligt. Licht je werkwijze toe.

Elke iso-afstandslijn bestaat uit drie cirkelbogen. Deze drie bogen sluiten op elkaar aan in de punten L (links) en R(rechts) Zie onderstaande figuur.

Voor alle punten L geldt: LM + LE = 9.

Toon dit aan.

Uit LM + LE = 9 volgt dat de punten L op een ellips met brandpunten E en M liggen. Evenzo liggen de punten R op een ellips met brandpunten F en M. De twee ellipsen snijden elkaar in twee punten die, vanwege de symmetrie van de figuur, op de middelloodlijn van EF liggen. Een van deze snijpunten is het midden T van EF. Het andere snijpunt is S. Zie onderstaande figuur.

Bereken de afstand MS.

De functie f(x) = e^x

Op de grafiek van de functie f(x) = e^x liggen de punten A en B met x-coördinaten a en a + 1. Zie de figuur hiernaast. Het gebied dat wordt ingesloten door de grafiek van f, de horizontale lijn door B en de verticale lijn door A is in deze figuur grijs aangegeven.

4p	10.	Bereken exact de waarde van a waarvoor de oppervlakte van dit gebied gelijk is aan 3.

Als a toeneemt, neemt de richtingscoëfficiënt van de lijn AB ook toe.

4p	11.	Bereken voor welke waarden van a de richtingscoëfficiënt van AB kleiner is dan 1. Rond in je antwoord de grenswaarde af op twee decimalen.

In de volgende vragen is a = 1, dus A is het punt (1, e) en B is het punt (2, e²).

4p	12.	Bereken de lengte van de grafiek van f tussen A en B.

P en Q zijn de loodrechte projecties van A op de x-as en de y-as. De rechthoek OPAQ wordt door de grafiek van f verdeeld in twee stukken. Zie de figuur hiernaast. Beide stukken wentelen we om de x-as.

6p	13.	Bereken exact het verschil tussen de inhouden van de twee omwentelingslichamen.

Driehoeken plakken

We maken een figuur die uit oneindig veel gelijkzijdige driehoeken bestaat. We beginnen met een gelijkzijdige driehoek met zijde 3 cm. Rechtsboven plakken we er een gelijkzijdige driehoek aan met zijde 2,7 cm. Zo plakken we er steeds rechtsboven een gelijkzijdige driehoek aan, de ene keer met de top naar beneden, de andere keer met de top naar boven. De zijden van de nieuw te plakken driehoek zijn 0,9 keer zogroot als de zijden van de vorige driehoek die werd geplakt. In onderstaande figuur zie je de figuur in opbouw: na zeven keer plakken. Na elke keer plakken komt de figuur dichter bij de finishlijn. We plakken oneindig vaak.



6p	14.	Onderzoek met behulp van een berekening of de figuur op den duur de finishlijn overschrijdt.

Brievenweger

Op de foto hiernaast zie je een brievenweger.
Als je een gewicht (een brief) op het schaaltje legt kun je op de witte schaalverdeling het gewicht ervan aflezen.
In de onderstaande figuur is schematisch een soortgelijke brievenweger weergegeven met een voorwerp dat y gram weegt.
De pijl waarbij je het gewicht afleest ligt loodrecht onder het draaipunt D. De ballast zorgt ervoor dat het verbindingsstuk DE verticaal staat als er niets op het schaaltje ligt.
De verbinding tussen de stukken ED en DC is vast.

Als een voorwerp van y gram op het schaaltje geplaatst wordt, draait het verbindingsstuk CDE om punt D over een hoek van a radialen. De cirkelvormige schaalverdeling en de ballast draaien ook en de pijl wijst op de schaalverdeling het getal y aan. Het schaaltje blijft horizontaal door de scharnieren in de punten A, B en C. Zie de figuur hierboven.
Bij deze brievenweger kan met behulp van statica de volgende formule worden afgeleid (a in radialen):

15.

Bepaal door meten en berekenen de waarde van y. Gebruik daarvoor bovenstaande figuur. Rond je antwoord af op een gehele waarde. Licht je antwoord toe.

16.

Bereken exact de waarde van α waarvoor geldt y = 70

Voor de afgeleide ^d^y/_dα geldt de formule:

17.

Toon dit aan.

Op de schaalverdeling kun je alle streepjes van 1, 2, 3, ... tot 100 gram aangeven. De onderlinge afstanden tussen die streepjes zijn verschillend. In de buurt van een zekere waarde van α liggen de streepjes het verst van elkaar. Bij deze waarde van α is ^d^y/_dαminimaal.

18.

Bereken in twee decimalen nauwkeurig de waarde van α waarvoor ^d^y/_dα minimaal is.

Spiegeltjes op een cirkel.

De punten A en B liggen op een cirkel. In het punt S op de cirkel plaatsen we een vlak spiegeltje zo dat de lichtstraal vanuit A wordt weerspiegeld naar B. De hoek α die AS met de spiegel maakt is dus gelijk aan de hoek β die SB met de spiegel maakt. Zie de bovenste figuur hiernaast. Als we de lijn van de spiegel in S verlengen snijdt deze de cirkel in punt C. Zie de middelste figuur hiernaast. Er geldt: ∠BAC = ∠ABC

4p	19.	Toon dit aan

De omgekeerde bewering is ook waar: als in driehoek ABC geldt ∠BAC = ∠ABC, dan geldt voor elk punt S op de omgeschreven cirkel van driehoek ABC α = β, waarbij α en β de hoeken zijn die respectievelijk AS en BS met lijn CS maken. In de onderste figuur hiernaast zijn twee andere punten A en B op de cirkel getekend en verder nog twee punten P en Q op de cirkel. In P en Q willen we een spiegeltje zo plaatsen dat in elk van beide spiegeltjes lichtstralen van A weerkaatst worden naar B.

4p	20.	Hoe kun je de omgekeerde bewering gebruiken om de juiste stand van de spiegeltjes bij P en Q te tekenen? Licht je antwoord toe met een tekening.

1.	Uit de figuur volgt sinα = ^overstaand/_schuin = ^x/_r Invullen, samen met c = 650, levert V = 650 • ¹/_r • ^x/_r = ^650x/_r2 .....(1) Pythagoras levert x² + 3² = r² ofwel r² = x² + 9 De r² in formule (1) hierdoor vervangen geeft het gevraagde resultaat.

2.	⇒ 900 + 100x² = 650x ⇒ 100x² - 650x + 900 = 0 Het kan nu met de ABC-formule (a = 100, b = -650, c = 900) of zó: x² - 6,5x + 9 = 0 ⇒ (x - 4,5) • (x - 2) = 0 ⇒ x = 4,5 of x = 2 Voor de hoogte van de balk moet dus gelden 2 ≤ x ≤ 4,5

3.	Als V maximaal is moet gelden V'= 0. Met de productregel: Dat is nul als de teller nul is: 650 • (9 + x²) - 650x • 2x = 0 ⇒ 5850 + 650x² - 1300x² = 0 ⇒ 5850 - 650x² = 0 Þ 650x² = 5850 ⇒ x² = 9 ⇒ x = 3 (of x = -3 maar dat is gezien de context onmogelijk). Conclusie: de hoogte x = 3 m

4.	Voor de speelvelden moet je er 4 van de 8 kiezen, dus dat kan op 8 nCr 4 manieren Voor de scoringsvelden moet je er 2 van de 4 kiezen en dat kan op 4 nCr 2 manieren. Het totaal aantal manieren is dan (8 nCr 4) • (4 nCr 2) = 70 • 6 = 420

5.	De wedstrijden met lengte 4 zijn VVPD en PMPD De kans op VVPD is ⁴/₈ • ³/₇ • ⁴/₆ • ²/₄ = ¹/₁₄ De kans op PMPD is ⁴/₈ • ²/₄ • ³/₇ • ²/₃ = ¹/₁₄ Samen is dat ²/₁₄

6.	Als Ruud eerlijk speelt heeft hij elke keer kans 0,5 dat hij als eerste vakje een P open krast. Het aantal keren dat dat gebeurt is dan binomiaal verdeeld met n = 10 en p = 0,5 Het gaat om P(X ≥ 8) want dan wordt Ruud beschuldigd (minstens 8 keer) terwijl hij wel eerlijk speelt (p = 0,5). P(X ≥ 8) = 1 - P(X ≤ 7) = 1 - binomcdf(10, 0.5, 7) = 0,055


7.	De iso-afstandslijn van een punt (M in dit geval) tot een cirkelboog is een cirkel met hetzelfde middelpunt als de cirkelboog. De iso-afstandslijnen van M tot AB, DC en BC zullen dus cirkels zijn met middelpunten respectievelijk E, F en M. Teken eerst twee cirkels met straal ME en MF en middelpunten E en F. Noem P het snijpunt van ME met boog AB, dan is de gezochte afstand MP. Teken punt Q op MR zodat QR = MP (zie onderstaande figuur). Het derde deel van de iso-afstandslijn is dan een deel van een cirkel met straal MQ en middelpunt M. Daarmee is de rode iso-afstandslijn hieronder te tekenen.


8.	De afstand van L tot AB is gelijk aan LE - 3 De afstand van L tot BC is gelijk aan 6 - LM Deze afstanden moeten gelijk zijn, dus LE - 3 = 6 - LM ⇒ LE + LM = 9

9.	Als S op de ellipsen ligt geldt SM + SE = 9 (dat staat direct boven opgave 8: S is immers ook een L-punt) Daaruit volgt SE = 9 - SM Verder is ST = 3 + SM en ET = 6 Pythagoras in driehoek ETS: 6² + (3 + SM)² = (9 - SM)² 36 + 9 + 6SM + SM² = 81 - 18SM + SM² 45 + 6SM = 81 - 18SM 24SM = 36 SM = 1,5


10.	De horizontale lijn door B heeft vergelijking y = e^a^{+ 1} Oppervlakte: 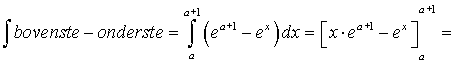= (a + 1) • e^a^{+ 1} - e^a^{+ 1} - (a • e^{a + 1} - e^a) = a • e^a^{+ 1} + e^a^{+ 1} - e^a^{+ 1} - a • e^a^{+ 1} + e^a= e^a e^a= 3 geeft a = ln3

11.	Voor de richtingscoëfficiënt van AB geldt: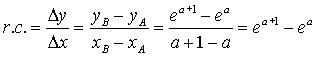 e^a^{+ 1} - e^a = 1 ⇒ e^a • e - e^a = 1 ⇒ e^a •(e - 1) = 1 ⇒ e^a = ¹/_(e_{- 1)} ⇒ a = ln(¹/_{(e - 1)}) ≈ -0,54 De r.c. is kleiner dan 1 als a < -0,54

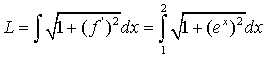
12.	Gebruik de GR: Y1 = √*(1 + (e^x)² ) en dan calc - 7 geeft lengte L* ≈ 4,79

13.	Lijnstuk AQ wentelen om de x-as geeft een cilinder met hoogte 1 en straal grondvlak e De inhoud daarvan is π • e² • 1 = πe² De grafiek van f wentelen om de x-as geeft inhoud: 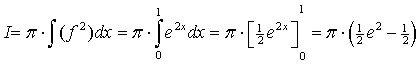Het tweede omwentelingslichaam is dan πe² - π • (0,5e² - 0,5) = 0,5πe² + 0,5π Het scheelt π

14.	De som van de bovenrand is gelijk aan 2,7 + 0,9² • 2,7 + 0,9⁴ • 2,7 + ... Dat is een meetkundige rij met reden 0,9² = 0,81 De som ervan is (formulekaart): S = ^2,7/_{(1 - 0,81)} = 14,21 Dat is meer dan 14 dus de finishlijn wordt wel overschreden.


15.	Met een geo-driehoek is te meten dat α ≈ 30º 2π = 360º dus 30º = ¹/₆π. Invullen in de formule geeft y ≈ 36

16.	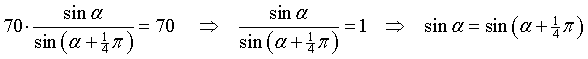Daaruit volgt α = α + ¹/₄π of α = π - (α + ¹/₄π) (we vergeten de periode modulo 2π voor het gemak) Dus 0 = ¹/₄π of 2α = ³/₄π De laatste geeft α = ³/₈π.

17.	Met de quotiëntregel: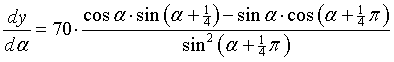 De teller lijkt eigenlijk best veel op de formule sin(t - u) = sint cosu - cost sinu van de formulekaart als je maar neemt t = α + ¹/₄π en u = α. Dan is t - u = α + ¹/₄π - α = ¹/4π Vervang de teller daardoor en de gevraagde formule staat er al!

18.	Voer de formule voor ^d^y/_d_α in de GR in bij Y1, en gebruik calc - minimum om het minimum te vinden. Neem bijv. Xmin = 0 Xmax = 3 Ymin = 0 Ymax = 100 Dat geeft α ≈ 0,79 radialen

19.

∠BAC = β (beiden de omtrekshoek van BC)
∠ACB = ∠ASB = γ (beiden de omtrekshoek van AB)
α + β + γ = 180 (samen gestrekte hoek bij S)
in driehoek ACB is de som van de hoeken ook 180, dus moet ∠ABC = α = β
∠ABC en ∠BAC zijn beiden gelijk aan β, dus gelijk aan elkaar.

20.

Teken de middelloodlijn van AB, die snijdt de cirkel in C (aan dezelfde kant van AB als P).
Dan is driehoek ABC gelijkbenig, dus zijn de basishoeken BAC en ABC gelijk.
Richting CP geeft de stand van de spiegel.

De andere spiegel gaat analoog.

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

VWO WB12, 2007 - I