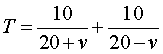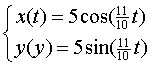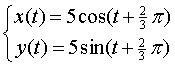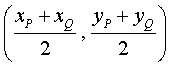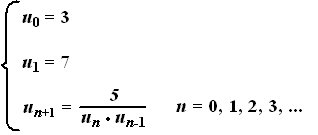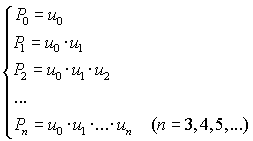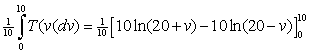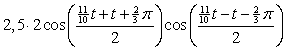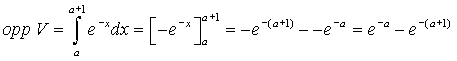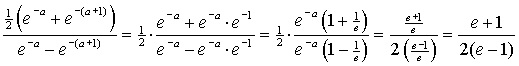VWO WB12, 2005 - II
Reistijd
Een boot vaart op een rivier van A naar B en terug. De afstand tussen A en B is 10 km. De boot vaart altijd met een snelheid van 20 km/uur ten opzichte van het water. De rivier stroomt in de richting van A naar B. Zie de figuur hiernaast.

Tijdens de reis van de boot van A naar B en terug is de stroomsnelheid van de rivier constant. We noemen de stroomsnelheid v (in km/uur)
Een voorbeeld: als v = 5 dan vaart de boot op de heenreis met een snelheid van 25 km/uur ten opzichte van de oever en op de terugreis met een snelheid van 15 km/uur ten opzichte van de oever.
De totale reistijd T van de retourtocht wordt gegeven door:

Hierbij is T in uren en v in km/uur met 0 < v < 20.
3p

1.

 Toon aan dat deze formule juist is.

 
3p

2.

 Bereken bij welke waarde van v de totale reistijd van een retourtocht 2 uur is. Geef je antwoord in twee decimalen nauwkeurig.

 
Als de stroomsnelheid van de rivier groter wordt neemt de totale reistijd van een retourtocht toe.
6p

3.

 Toon dit aan met behulp van de formule van de afgeleide functie van T.

 
Veronderstel dat v varieert tussen 0 en 10 km/u. en dat alle waarden van 0 tot en met 10 even vaak voorkomen. De gemiddelde reistijd kun je dan benaderen door T uit te rekenen voor v = 0, v = 0.1,  v = 0.2, v = 0.3, enzovoort tot en met v = 10 en van de reistijden het gemiddelde te nemen. 
5p

4.

 Bereken de gemiddelde reistijd met deze benaderingswijze. Geef je antwoord in minuten nauwkeurig.

 
Je kunt de gemiddelde reistijd ook uitrekenen met een integraal.
6p

5.

 Toon langs algebraïsche weg aan dat de gemiddelde reistijd gelijk is aan ln3 uur.

 
Maximumsnelheid
De snelheidsmeter van een auto geeft meestal niet precies aan wat de werkelijke snelheid is waarmee de auto rijdt. Voor een bepaald type snelheidsmeter geldt het volgende: als de snelheidsmeter een snelheid van v km/u aangeeft is de waarde van de werkelijke snelheid normaal verdeeld, waarbij het gemiddelde gelijk is aan v en de standaardafwijking gelijk is aan 1,5% van dat gemiddelde.

Bij snelheidscontrole wordt een marge aangehouden van 3%. Dus bijvoorbeeld bij een maximumsnelheid van 100 km/u wordt er beboet bij snelheden van 103 km/u en hoger.

Van een auto is de snelheidsmeter van bovenstaand type. De bestuurder rijdt volgens de meter steeds met precies  de toegestane maximumsnelheid.

Stel dat de toegestane maximumsnelheid 70 km/u is. De kans dat de werkelijke snelheid van de bestuurder zo groot is dat hij voor een boete in aanmerking komt is dan, afgerond op 3 decimalen, gelijk aan 0,023. 
4p

6.

 Toon dit aan.

 
De kans dat hij in aanmerking komt voor een boete is bij elke toegestane maximumsnelheid even groot
4p

7.

 Toon dit aan

 
De bestuurder passeert in een jaar 200 keer een elektronisch bord dat waarschuwt wanneer men te hard rijdt, dat wil zeggen wanneer men de boetegrens overschrijdt. De kans dat de bestuurder voor een boete in aanmerking komt is telkens 0,023.
4p

8.

 Bereken de kans dat de bestuurder van die 200 keer meer dan 2 keer gewaarschuwd wordt.

 
Achtervolging
Op tijdstip t = 0 beginnen de punten P en Q met een eenparige cirkelbeweging.
De bewegingsvergelijkingen zijn:
voor P: en voor Q:
Hierbij is t in seconden en zijn x(t) en y(t) in centimeters.
In de figuur hiernaast staat de beginsituatie op schaal getekend.

Tijdens de beweging wordt Q telkens door P ingehaald.

 

4p

9.

 Bereken na hoeveel seconden Q voor het eerst door P wordt ingehaald.

 
Het punt M is het midden van lijnstuk PQ.
De coördinaten van M zijn:

De bewegingsvergelijkingen van  M zijn van de vorm:
5p

10.

 Geef een formule voor φ  uitgedrukt in t. Licht je antwoord toe.

 

 

Snijpunten met een ellips.
Hiernaast is een cirkel  c getekend met middelpunt M en een middellijn AB.
Punt F is een punt binnen de cirkel.
De conflictlijn van cirkel c en punt F is een ellips.

4p 11. Teken in deze figuur de snijpunten van deze ellips e en lijn AB. Licht je werkwijze toe.

 
Hieronder is de cirkel nogmaals getekend met M en F en ellips e.
Verder is een willekeurige middellijn XY getekend.
De snijpunten van de ellips e en lijn XY zijn P en Q.

∠PFQ noemen we α en ∠XFY noemen we β.
Tussen α en β bestaat het volgende verband:  β = 1/2α + 90º
5p

12.

 Bewijs dit.

 
Exponentiële functie
Gegeven is de functie f(x) = e-x .
Op de grafiek van  f  liggen de punten A en B met x-coördinaten  xA = 0  en xB = 1
Zie de figuur hiernaast.

Op de grafiek van f  ligt een punt C waarin de raaklijn aan de grafiek van f evenwijdig is aan het lijnstuk AB.
5p

13.

 Bereken de x-coördinaat van C. Rond af op twee decimalen.

 
De lijn x = a snijdt de x-as in P en de grafiek van f in S., de lijn x = a + 1 snijdt de x-as in Q en de grafiek van f in R. Het gebied begrensd door de grafiek van  f en de lijnstukken PS, PQ en QR noemen we V. Het trapezium PQRS noemen we W. Zie de volgende figuur.

7p

14.

 Toon aan dat de verhouding  oppervlakte van W/oppervlakte van V onafhankelijk is van a.

 

 

Vijf punten op een cirkel.
Gegeven zijn de cirkels c1 en c2 met middelpunten M1 en M2 en stralen r1 en r2.
Cirkel c1 is groter dan cirkel c2. Cirkel c2 ligt geheel buiten cirkel c1. Het verbindingslijnstuk M1M2 snijdt c1 in punt A en c2 in punt B. Zie onderstaande figuur. De lengte van lijnstuk AB is gelijk aan d. In de figuur is ook nog een derde cirkel c3 getekend, met middelpunt D en straal d.

We plaatsen c3 zo, dat hij c1 en c2 raakt. De raakpunten noemen we E en C.
Dan ligt punt E op M1D en punt C op M2D. Zie onderstaande figuur.

Vierhoek ABDE is een koordenvierhoek.
6p

15.

 Toon dit aan.

 
4p

16.

 Bewijs dat de vijf punten A, B, C, D en E op één cirkel liggen.

 

 

Periodieke rijen
Een rij u0, u1, u2, ... noemen we periodiek met periode p als p het kleinste positieve gehele getal is waarbij voor alle waarden van n geldt dat un + p = un.
Een voorbeeld van een periodieke rij met periode 4 is de rij 1, 5, 16, 12, 1, 5, 16, 12, 1, 5, 16, 12, ...

Gegeven is een rij   u0, u1, u2, ...  waarvoor geldt:
5p

17.

 Bereken u2005

 
We nemen in de bovengenoemde rij in plaats van 3 en 7 de staartwaarden a en b.  Dus u0 = a en u1 = b.
4p

18.

 Bereken exact voor welke waarde van a en welke waarde van b de rij periode 1 heeft.

 
We kiezen weer u0 = 3 en u1 = 7.
We definiëren een bij de rij u0, u1, u2, ... horende productrij  P0, P1, P2,... als volgt:
4p

19.

 Toon aan dat P3k + 1 = 21 • 5k , voor elke positieve gehele waarde van k.

 
OPLOSSING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
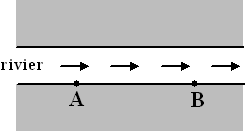
1. Snelheid van A naar B is 20 + v, dus de tijd is  10/(20 + v)
Snelheid van B naar A is 20 - v, dus de tijd is 10/(20 - v)
Dezen bij elkaar optellen geeft de gevraagde formule.
2. 10/(20 + v) + 10/(20 - v) = 2  ⇒- v) + 10(20 + v) = 2(20 - v)(20 + v)
 ⇒ 200 - 10v + 200 + 10v = 800 - 2v2  ⇒  2v2 = 400  ⇒  v2 = 200 ⇒  v = √200 ≈ 14,14 km/u
(de oplossing v = - √200 valt uiteraard af).

het kan uiteraard ook allemaal met de GR via intersect...
3. T = 10(20 + v)-1 + 10(20 - v)-1
T' = -1 • 10(20 + v)-2 - 1 • 10 • (20 - v)-2 • -1

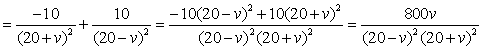
In de noemer staan allemaal kwadraten, dus die is altijd positief.
De teller is ook altijd positief omdat v > 0
Dus is de hele breuk altijd positief.
4. T(0) + T(0.1) + ... + T(10) moet uitgerekend worden, en dan gedeeld door 101.
u(n) = u(n - 1) + 10/(0,1n + 20) + 10/(20 - 0,1n)
Voer deze in de GR in bij  MODE - Seq en dan  Y=
nMin = 0, u(n) als hierboven, u(nMin) = 1
De som staat nu in de tabel bij u(100) en is ongeveer gelijk aan 111,03
Delen door 101 geeft 1,0993 uur dus dat is ongeveer 66 minuten.
5.
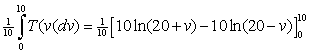
= (ln(30) - ln(10)) - (ln20)-ln(20)) = ln30 - ln10 = ln(30/10) = ln3
6. P(boete) = P(v > 72,1) = normalcdf(72.1, ∞ , 70, 1.05) ≈ 0,02275 ≈ 0,023
7. z = (x - μ)/σ
Noem de maximumsnelheid v, dan geldt:  x = 1,03 • v  en  μ = v  en  σ = 0,015v
Dat geeft z = (1,03v - v)/(0,015v) = 0,03v/0,015v = 2
Omdat z altijd gelijk is, is de oppervlakte onder de klokvorm dat ook.
8. binomiale verdeling met n = 200,  p = 0,023
P(meer dan 2) = 1 - P(2 of minder) = 1 - binomcdf(200,  0.023, 2) ≈  0,84
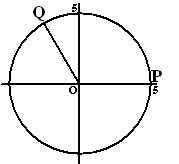
9. xP = xQ  ⇒  11/10t = t + 2/3π  ∨  11/10t = 2π - t - 2/3π ⇒  t = 20/3π  ∨  t = 40/63π
yP = yQ  ⇒  11/10t = t + 2/3π  ∨  11/10t = π - t - 2/3π ⇒  t = 20/3π  ∨  t = 10/63π

De eerste t die gelijk is, is  t = 20/3π ≈ 21 sec.

Op de natuurkunde manier:
de periode van P is 10/11 • 2π dus in 20/11p sec draait P over 2p rad, dat is  2/20/11 = 1,1 rad/sec
de periode van Q is 2π dus in 2π sec draait Q over 2π rad, dat is 1 rad/sec
per seconde loopt P dus 0,1 rad in.
P moet in totaal 2/3π rad inhalen, dus dat kost 20/3π seconden.
10. xM =1/2 • ( 5cos 11/10t + 5cos(t + 2/3π)) = 2,5 • (cos 11/10t + cos(t + 2/3π)) =

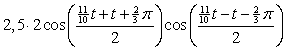
= 5 • cos(21/20t + 1/3π) • cos(1/20t - 1/3π)

Op dezelfde manier:  yM = 5 • sin(21/20t + 1/3π) • cos(1/20t - 1/3π)

Kennelijk moet gelden  φ = 5cos(1/20t - 1/3π)
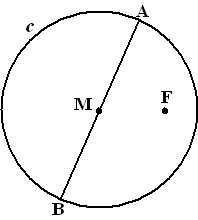
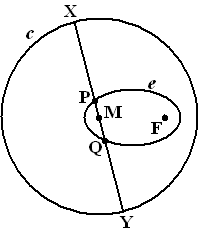
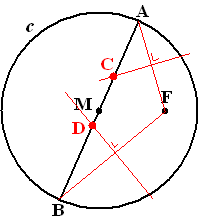
11. Noem het snijpunt met MA punt C. De afstand van C tot de cirkel is dan CA, dus moet gelden CA = CF.
C ligt dus op de middelloodlijn van AF.

Op dezelfde manier ligt D op de middelloodlijn van FB.

12. Noem ∠XFP gelijk aan g. Dan is ook ∠FXP = γ want driehoek PXF is gelijkbenig omdat PX = PF.
Noem ∠YFQ gelijk aan d. Dan is ook ∠QFY = δ want driehoek FQY is gelijkbenig omdat QF = QY.
Bekijk nu driehoek XFY.
De som van alle hoeken daarin is γ + γ + α + δ + δ = 2γ + α + 2δ = 180º
Daaruit volgt  γ + δ + 1/2α = 90º  ofwel  γ + δ + α - 1/2α = 90º  ⇒  β - 1/2α = 90º  ⇒  β = 1/2α + 90º. 
13. De helling van AB is  (1/e - 1)/(1 - 0) =  1/e - 1
f '(x) = -e -x
 -e -x = 1/e - 1  ⇒  -1/ex = (1-e)/e  ⇒  ex = e/(e - 1)  ⇒  x = ln(e/e - 1)  ≈ 0,46

Maar deze laatste regel mag natuurlijk ook met de GR (intersect)...
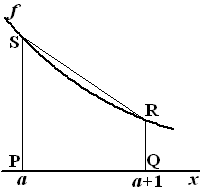
14. PS = f(a) = e -a  en  RQ = f(a + 1) = e -(a + 1)
oppervlakte W = rechthoek + driehoek = 1 • e -(a + 1)  + 1/2 • 1 • (e -a - e -(a + 1)) = 1/2e -a + 1/2e -(a + 1)

Oppervlakte V:

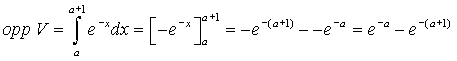
De verhouding daartussen:

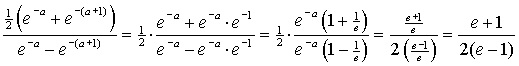
en dat is duidelijk onafhankelijk van a.
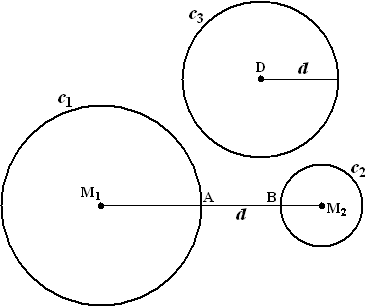
15. Driehoek M1EA is gelijkbenig, want M1E = M1A = r1. Dus is ∠M1EA = ∠M1AE.
Maar dan is ∠DEA = 180º- ∠M1EA = 180º- ∠M1AE = ∠BAE.  Noem deze hoeken α.

Driehoek M1DB is ook gelijkbenig, want M1D = M1B = r1 + d
Dus is ∠M1DB = ∠M1BD. Noem deze hoeken β.

In vierhoek AEDB geldt nu α + α + β + β = 360  ⇒  α + β = 180º  dus twee hoeken tegenover elkaar zijn 180º. Dan is AEBD een koordenvierhoek.
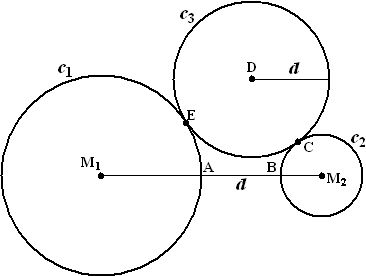
16. Door de gelijkbenige driehoeken M2CB en M2DA te bekijken kun je op precies dezelfde manier als in opgave 15 bewijzen dat ADCB ook een koordenvierhoek is.
De cirkel door AEDB is de omgeschreven cirkel van driehoek ADB
De cirkel door ADCB is ook de omgeschreven cirkel van driehoek ADB.
Kortom; alle vijf de punten liggen op deze omgeschreven cirkel. 
17. de rij wordt:  3, 7, 5/21, 3, 7, 5/21, ....
u0 = u3 = u6 = ... = 3
u1 = u4 = u7 = ... = u2005 = 7   (want 2004 is een drievoud) 
18. Als de rij periode 1 heeft, is a = b  dus is de rij  a a a a  .....
De recursievergelijking geeft dan  a = 5/(a • a)  dus  a3 = 5  en a = b = 3√5
19. P0 = 3
P1 = 3 • 7
P2 = 3 • 7 • 5/21
P3 = 3 • 7 • 5/21 • 3
P4 = 3 • 7 • 5/21 • 3 • 7
P3k + 1 = (3 • 7 • 5/21) • (3 • 7 • 5/21) • (3 • 7 • 5/21) • (3 • 7 • 5/21) •......• 3 • 7
daarbij staan er k factoren met haakjes
elk van die factoren is 5
dus er staat  P3k + 1 = 5k • 21