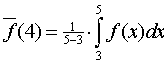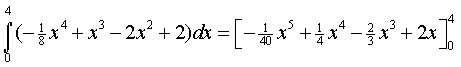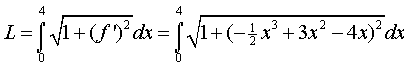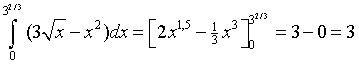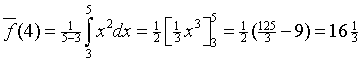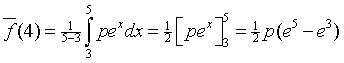VWO WB1, 2006 - II
Drinkbak.
In de figuur hieronder staat een tekening van een drinkbak voor dieren. De bak bestaat uit drie delen: een rechthoekige metalen plaat die gebogen is tot een symmetrische goot, een voorkant en een achterkant die aan de goot gelast zijn.
De bak is 20 dm lang, 4 dm breed en 2 dm diep.

In de figuur hieronder is het vooraanzicht van de goot getekend in een assenstelsel.

De gebogen vorm van de goot is de grafiek van de functie:
  f(x) = -1/8x4  + x3 - 2x2 + 2  (x en y in dm, en 0 ≤ x ≤ 4)
4p

1.

 Toon algebraïsch aan dat de helling van de grafiek van f gelijk is aan 0 voor x = 0 en voor x = 4.

 
De waterspiegel heeft de vorm van een rechthoek, waarvan de lengte 20 dm is. De breedte van de waterspiegel varieert met de waterhoogte. In de figuur hieronder is in het assenstelsel het vooraanzicht van de bak getekend bij een bepaalde waterhoogte.

3p

2.

 Bereken de waterhoogte als de breedte van de waterspiegel 2,4 dm is.

6p

3.

 Bereken in liters nauwkeurig hoeveel water de bak bevat als hij tot de rand gevuld is.

5p

4.

 

 Bereken in dm2 nauwkeurig de oppervlakte van de rechthoekige plaat waarvan het gebogen deel van de drinkbak gemaakt is.
   

 

Parkeertarief.
's Zaterdags gaat Anneke altijd winkelen in de stad. Ze parkeert dan haar auto aan de rand van het centrum. De parkeermeter rekent daar met hele kwartieren en er moet vooraf betaald worden. Elk kwartier of een deel daarvan kost €0,30. Op grond van het lijstje met inkopen die ze wil doen maakt Anneke een schatting van de tijdsduur voor het parkeren. Door allerlei omstandigheden (onder andere bediening, drukte) is de werkelijke tijdsduur vaak anders.
We nemen aan dat de werkelijke tijdsduur bij benadering normaal verdeeld is, waarbij het gemiddelde gelijk is aan haar schatting; voor de standaardafwijking geldt het volgende:  als de schatting t uren bedraagt dan is de standaardafwijking gelijk aan 1/6√t uur.

Op een zaterdag schat Anneke 2,5 uur nodig te hebben voor haar inkopen en doet dus €3,00 in de parkeermeter.
4p

5.

 Bereken de kans dat achteraf - als ze terugkomt bij haar auto - zal blijken dat ze precies €0,30 minder in de parkeermeter had mogen doen.

Door bij een schatting van 2,5 uur parkeren €3,00 in de parkeermeter te doen, loopt Anneke ook het risico dat ze te weinig betaalt.
5p

6.

 Bereken hoeveel geld Anneke tenminste in de meter moet doen opdat ze minder dan 5% kans loopt dat ze te weinig betaalt.

Als Anneke onvoldoende parkeergeld betaalt loopt zij kans op een parkeerboete. Ieder uur heeft elke geparkeerde auto waarvan de parkeertijd verlopen is, een kans van 16% op een parkeerboete. Eenmaal beboet krijgt een auto geen tweede boete.
4p

7.

 Bereken de kans dat Anneke een parkeerboete krijgt wanneer zij 3 uur lang onbetaald parkeert.

 

Snijden en schuiven.
Voor x ³ 0 zijn gegeven de functies  f (x) =  x2  en  g(x) = 3√x.
In de figuur hiernaast staat van beide functies een deel van de grafiek getekend.

De grafieken van f en g sluiten een vlakdeel V in.

5p

8.

 Bereken de oppervlakte van V.

De verticale lijn x = a snijdt de grafiek van g in het punt A,  de grafiek van f  in het punt B en de x-as in punt C. Voor een bepaalde waarde van a ligt B midden tussen A en C.
4p

9.

 Bereken exact voor welke waarde van a dit het geval is.
De grafiek van f wordt omhooggeschoven totdat hij raakt aan de grafiek van g.

6p

10.

 Bereken met behulp van differentiëren in twee decimalen nauwkeurig hoeveel de grafiek van f dan omhooggeschoven is.

α - baan
De plaats van een bewegend punt P in een assenstelsel wordt gegeven door:
x(t) = cos2t  en  y(t) = cos3t, waarbij t de tijd voorstelt, met 0 ≤ t ≤ π.
De baan van het punt P lijkt op de Griekse letter α. Zie volgende figuur.

Op het tijdstip t = 0 bevindt P zich in (1,1), dus even ver van de x-as als van de y-as.
4p

11.

 Bereken het eerste tijdstip na t = 0 waarop P zich wéér even ver van de x-as als van de y-as bevindt.

Tussen t = 0 en t = π beweegt P éénmaal over de baan. Gedurende twee tijdsintervallen bevindt P zich boven de lijn  y = 1/2. Zie onderstaande figuur.

4p

12.

 Bereken de totale tijd dat P zich boven de lijn y = 1/2 bevindt.

Tijdens de beweging verandert de snelheid van het punt P.
5p

13.

 Onderzoek of de grootste snelheid van het punt P wordt bereikt op het tijdstip t = 1/2p.


Levensduur van chips.
In elektronische apparatuur worden veel chips gebruikt. Om de levensduur van chips te bepalen kan men niet gewoon wachten tot ze stukgaan. Dat kan namelijk wel 20 á 30 jaar duren! Daarom past men zogenaamde stress-methoden toe: men onderwerpt de chips aan extreme omstandigheden, bijvoorbeeld hoge temperatuur, zodat ze sneller stukgaan. Vervolgens kan men de onder extreme omstandigheden gevonden levensduur terugrekenen naar de levensduur onder normale omstandigheden.

Bij hoge-temperatuurstress werkt men met het model van Arrhenius:

Hierbij is g de levensduur (in jaren), T de temperatuur (in Kelvin) en a een constante.

De levensduur van een chip van type A blijkt bij een temperatuur van 373 Kelvin 0,1 jaar te zijn.
4p

14.

 Toon door berekening aan dat bij kamertemperatuur (293 Kelvin) de levensduur van zo'n chip ongeveer 28 jaar is.

Neem bij de volgende vraag a = 7700.
Een gebruiker wil weten hoe snel g bij toenemende temperatuur verandert als T = 293.
4p

15.

 Bereken deze snelheid met behulp van differentiëren.

Neem aan dat de levensduur van chips van type B bij gebruik bij kamertemperatuur normaal verdeeld is met een verwachtingswaarde m van  8,0 jaar en een standaardafwijking s van 2,0 jaar.

Een klant koopt 500 chips van type B.
4p

16.

 Hoeveel van deze chips zullen naar verwachting binnen 5 jaar stukgaan?

Van de chips van type B vermoedt men dat m kleiner is dan 8,0 jaar. Om dat te onderzoeken past een laboratorium hoge-temperatuurstress toe op 50 chips van type B.
Als de levensduur van de chips van dit type normaal verdeeld is met m = 8,0 en s = 2,0 dan is de gemiddelde levensduur van de chips bij een steekproef van 50 chips normaal verdeeld met m = 8,0 en s = 2,0/Ö50.
Met de resultaten van het laboratorium heeft men berekend dat deze chips bij kamertemperatuur een gemiddelde levensduur van 7,2 jaar gehad zouden hebben. De aanname dat de levensduur van chips van type B bij gebruik bij kamertemperatuur normaal verdeeld is met een verwachtingswaarde m van 8,0 jaar en een standaardafwijking s van 2,0 jaar noemt men de nulhypothese.
5p

17.

 Geeft deze uitkomst van 7,2 jaar voldoende aanleiding om bij een significantieniveau van 1% de nulhypothese te verwerpen?

Gemiddelde functiewaarde.
In de figuur hieronder is de grafiek getekend van een functie f
De gemiddelde functie waarde van f op het interval [3, 5] is:
De uitkomst noemen we dus  

Zie volgende figuur

Bij de volgende vraag kiezen we voor f de functie f(x) = x2
4p

18.
Bereken de exacte waarde van 
We kiezen nu voor f de functie  f(x) = p • ex .
Voor een bepaalde waarde van p geldt: 
4p

19.

 Bereken deze waarde van p in twee decimalen nauwkeurig.


OPLOSSING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
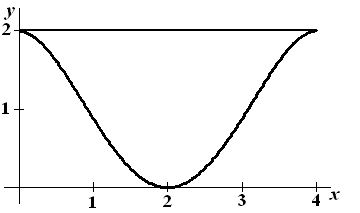
1. f '(x) = -1/2x3 + 3x2 - 4x
f '(0) = 0  en f '(4) = -32 + 48 - 16 = 0  
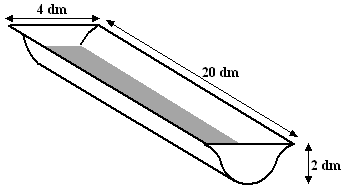
2. Als de breedte 2,4 is, is dat horizontaal vanaf x = 2 aan beide kanten 1,2 dm.
Dat is dus bij de punten x = 0,8 en x = 3,2.
f(0,8) = 1,1808 en dat is de waterhoogte.
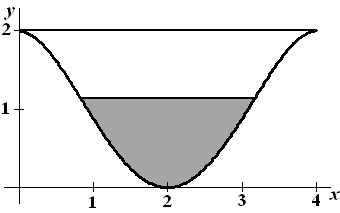
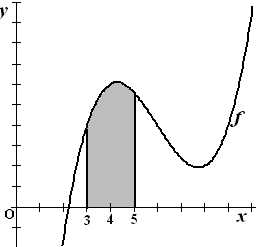
3. De oppervlakte onder de grafiek van f tussen x = 0  en x = 4 is gelijk aan:

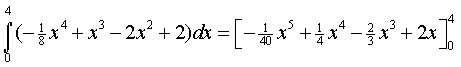
en dat is 56/15.
De oppervlakte van de voorkant van de waterbak is dan 8 - 56/15 = 64/15.
De inhoud is dan 20 • 64/15 = 851/3 dm3 
4. De breedte van de plaat is de lengte van de grafiek van f.

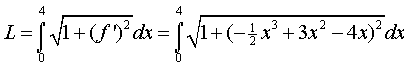
invoeren in de GR  geeft een lengte van ongeveer 5,844 dm.
De oppervlakte wordt dan 5,844 • 20 ≈ 117 dm2 
5. Ze heeft betaald voor 10 kwartieren. Als dat precies 0,30 minder kon zijn heeft ze haar boodschappen in 9 kwartieren gedaan. Dat is van  2 tot 2,25 uur.
normalcdf(2, 2.25, 2.5, 1/6√2.5) = 0,1425
6. normalcdf(X, 1000..., 2.5, 1/6√2.5) = 0,05
Y1 = normalcdf(X, 1000..., 2.5, 1/6√2.5) en Y2 = 0,05
window bijv.  Xmin = 0, Xmax = 5,  Ymin = 0, Ymax = 0,1
intersect geeft X = 2,933 uur.
Dus moet ze tenminste voor 12 kwartieren in de meter doen, en dat is €3,60
7. De kans dat ze een uur géén boete krijgt is 84%
De kans dat de 3 uur géén boete krijgt is 0,843 = 0,592704
De kans dat ze wel een boete krijgt is dan 1 - 0,592704 = 0,407296
8. Snijpunt:  x2 = 3√x  ⇒  x2 - 3√x = 0  ⇒  √x • (x1,5 - 3) = 0  ⇒  √x = 0  ∨  x1,5 = 3
Dat geeft als tweede snijpunt  x = 32/3 (≈ 2,08)

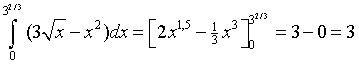
(het mag ook met de GR natuurlijk...)
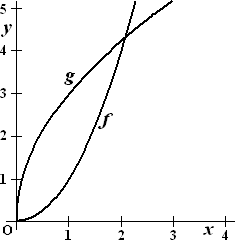
9. B ligt midden tussen A en C als  g(a) = 2 • f(a)
3√a = 2a2  ⇒  9a = 4a4  ⇒  9a - 4a4 = 0  ⇒  a(9 - 4a3 ) = 0  ⇒  a = 0  ∨  a3 = 9/4
Behalve a = 0 is dus een tweede oplossing  a = 2,251/3 (≈ 1,31)
10. De functies raken elkaar als  f ' =  g '
2x = 0,5 • 3 • x-0,5   ⇒  x1,5 = 0,75  ⇒  x = 0,752/3  ≈ 0,83
f(0,83) = 0,6814  en g(0,83) = 2,7256  dus de grafiek van f moet 2,04 omhooggeschoven worden.
11. De afstand tot de assen is gelijk als x = y  of als x = -y

x = y  betekent  cos2t = cos3t  
⇒   2t = 3t (mod 2π)  ∨  2t = 2π - 3t (mod 2π)
⇒   t = 0  (mod 2π)  ∨  t = 2/5π  (mod 2/5π)

x = -y  betekent  cos 2t = -cos3t = cos(π - 3t)
 ⇒  2t = π - 3t  (mod 2π)  ∨  2π - 2t = π - 3t  (mod 2π)
 ⇒  t = 1/5π  (mod 2/5π)  ∨  t = π  (mod 2π)

Na t = 0 is het eerste tijdstip dus t = 1/5π
12. y = 0,5  ⇒  cos3t = 0,5 = cos(1/3π)
⇒  3t = 1/3π  (mod 2π)  ∨  3t = 2π - 1/3π  (mod 2π)
⇒  t = 1/9π   (mod 2/3π )  ∨  t = 5/9π  (mod 2/3π )
Tussen 0 en π geeft dat de oplossingen  t = 1/9π ,  5/9π en 7/9π
Het punt bevindt zich boven de lijn y = 0,5 als x ligt in het interval  [0, 1/9π〉 ∪ 〈5/9π, 7/9π〉
Dat is in totaal 1/3π (de eenheid in onbekend)
13. snelheid v = √((x' )2 + (y ')2 ) = √((-2sin2t)2 + (-3sin3t)2) = √(4sin22t + 9cos2(3t))
plot de grafiek van v
bij t = 0,5π geeft dat v = 3.
maar het maximum zit bij t ≈ 0,56 en t ≈ 2,58 en is gelijk aan ongeveer 3,48
conclusie: de grootste snelheid wordt NIET bereikt voor t = 0,5π.
14. 0,1 = 1,1 • 10-10 • ea/373  ⇒  909090909,1 =  ea/373   ⇒  a/373 = ln 909090909,1 ≈ 20,63
 ⇒  a ≈ 7694,23
g(293) = 1,1 • 10-10 • e7694,23/293 ≈  27,93 en dat is ongeveer 28 jaar.
15.
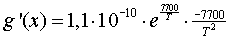
g'(293) ≈ -2,55
16. Voor één chip is de kans normalcdf(0, 5, 8.0, 2.0) = 0,0667755
Dus zullen 0,0667755 • 500 = 33 á 34 chips naar verwachting binnen 5 jaar stukgaan.
17. H0:  μ = 8,0,  σ = 2,0/√50
H1:  μ < 8,0
een eenzijdige toets met α = 0,01
De meting was 7,2 en de overschrijdingskans is dan  normalcdf(0, 7.2, 8.0, 2.0/√50) ≈ 0,0023
Dat is kleiner dan 0,01 dus de meting geeft WEL voldoende aanleiding H0 te verwerpen. 
18.
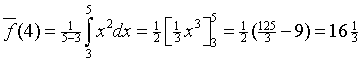
f(4) = 16,  dus dat geeft  161/3 - 16 = 1/3.
19.
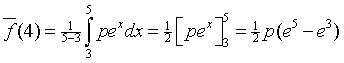
1/2p(e5 - e3 ) = 100  ⇒  64,1638p = 100  ⇒ p ≈ 1,56