VWO WB1,  2003  -  I
Lengte
Uit statistisch onderzoek is gebleken dat de volwassen Nederlandse mannen in 1999 gemiddeld 180,0 cm lang waren, en dat er een standaardafwijking van 12,8 cm was in de lengteverdeling. De normale verdeling met 180,0 als verwachtingswaarde en 12,8 als standaardafwijking past goed bij de werkelijke lengteverdeling. In de volgende vraag werken we met deze normale verdeling.
3p 1. Hoe groot is bij deze verdeling de kans dat vier willekeurig gekozen mannen alle vier korter dan 200 cm zijn?

 
Uit hetzelfde onderzoek bleek dat de volwassen Nederlandse vrouwen in dat jaar een gemiddelde lengte hadden van 167,0 cm. Verder bleek dat 27,8% van deze vrouwen langer was dan 177 cm. Neem aan dat bij de waargenomen lengteverdeling een normale verdeling past met 167,0 als verwachtingswaarde.
4p 2. Hoe moet je de standaardafwijking van deze normale verdeling kiezen om ervoor te zorgen dat de kans op een lengte groter dan 177 cm gelijk is aan  27,8%?

 
Zomertarwe
Een akker wordt op 1 april ingezaaid met zomertarwe. De tarwe wordt geoogst op 30 juli. In de 120 dagen tussen zaaien en oogsten groeien de planten niet steeds even hard. Aanvankelijk groeien de planten steeds sneller. Als de planten groter worden gaan ze elkaar meer hinderen waardoor de groeisnelheid nagenoeg constant wordt. Tegen het einde van het groeiseizoen gaan de tarweplanten steeds langzamer groeien.
Het gewicht van de tarweplanten in kilogrammen noemen we z. De tijd in dagen noemen we t; t = 0 op 1 april,  t = 120 op 30 juli.
z '(t) is de snelheid waarmee z groeit op tijdstip t (in kg/dag). Biologen hanteren voor de drie groeifasen wel het volgende model:
  • fase 1: exponentiële groei.  voor  0 ≤ t < 40  geldt:          z'(t) = 100 • e0,1(t - 40) 
  • fase 2: lineaire groei.          voor  40 ≤ t < 100 geldt          z'(t) = 100
  • fase 3: tanende groei          voor  100 ≤  t < 120  geldt      z'(t) = 100 • e-0,2(t - 100)
In de figuur hieronder staat de grafiek van z'
Bij elk tijdstip t1 in fase 1 is er een tijdstip t3 in fase 3 waarop de tarweplanten even snel groeien als op  t1.
4p 3. Bereken t3 exact als  t1 = 18

 
De hoeveelheid zaaigoed is 30 kg, dus  z(0) = 30

Er zijn getallen a en b, zo dat voor fase 1 geldt:  z(t) = a • e0,1(t - 40) + b
4p 4. Bereken a en b. Rond de waarde van b af op twee decimalen.

 
Op elk tijdstip t is het gewicht te bepalen met 

Er geldt  z(100) » 7011,68
6p 5. Toon dit aan.

 
3p 6. Bereken het gewicht van de tarweplanten op 30 juli.

 
Twee scharnierende vierkanten
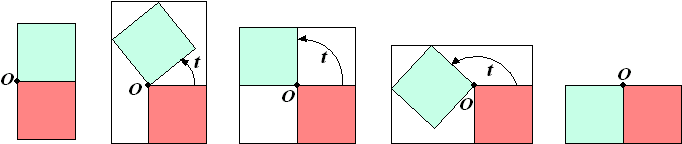
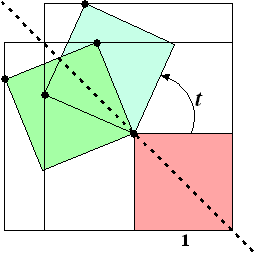
Twee vierkanten, beide met zijde 1, hebben het hoekpunt O gemeenschappelijk. Het onderste vierkant ligt vast. Het bovenste vierkant wordt om O gedraaid; t is de draaihoek in radialen. In de figuur hieronder zijn tussen de begin- en eindstand drie tussenstanden getekend. Om de twee vierkanten is steeds een zo klein mogelijke rechthoek getekend, met twee zijden langs het vaste vierkant.
De oppervlakte R van de omhullende rechthoek is een functie van de draaihoek t.
     
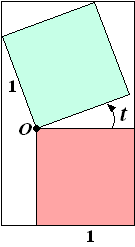
3p 7. Bereken de oppervlakte van R voor  t = 1/4π

 
Voor elke waarde van t tussen 0 en 1/2π geldt:  R(t) = (1 + sint) • (1 + sint + cost)
In de figuur hiernaast is de situatie getekend voor een waarde van t tussen 0 en 1/2π.
4p 8. Toon de juistheid van de formule aan voor elke waarde van t tussen  0 en 1/2π.

 
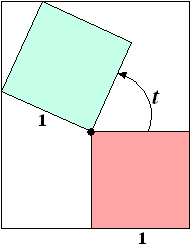
Er zijn tussen de begin- en de eindstand twee posities van de vierkanten waarvoor R(t) maximaal is. In de figuur hieronder is één van die posities getekend.
4p 9. Teken in deze figuur de andere positie van de vierkantjes waarvoor R(t) maximaal is. Licht je werkwijze toe.

 
3p 10. Toon met behulp van differentiëren aan dat  R'(0) = 3

 
Inhoud viervlak
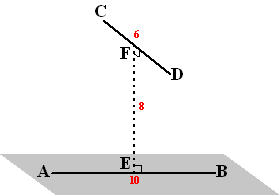
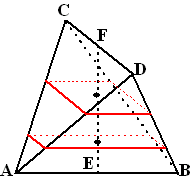
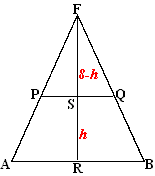
Lijnstuk AB ligt in een horizontaal vlak.
Lijnstuk CD is evenwijdig aan dat vlak, op afstand 8. Lijnstuk AB heeft lengte 10 en lijnstuk CD heeft lengte 6.
De lijnstukken AB en CD staan loodrecht op elkaar. E en F zijn de middens van AB en CD.
EF staat loodrecht op AB en op CD. Zie de figuur hiernaast.
Door de punten A en B te verbinden met de punten C en D ontstaat het viervlak ABCD.
In het viervlak brengen we horizontale doorsneden aan. Omdat AB en CD loodrecht op elkaar staan zijn de doorsneden rechthoeken. In de tweede figuur hiernaast is als voorbeeld op twee hoogten de doorsnede getekend. (De hoogte wordt gemeten langs het lijnstuk EF)
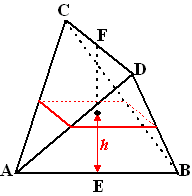
In de onderste figuur hiernaast is zo'n doorsnede op hoogte h boven het horizontale vlak  getekend, met  0 < h < 8.
Met behulp van driehoek ABF kan de lengte van de zijde van de rechthoek die in vlak ABD ligt, in h worden uitgedrukt.

De lengte van deze zijde is gelijk aan  10 - 5/4 • h.
4p 11. Toon dit aan.

 
De lengte van de andere zijde is gelijk aan  3/4 • h
5p 12. Onderzoek door een berekening of de doorsnede met de grootste oppervlakte een vierkant is.

 
Omdat we de oppervlakte van de doorsnede op elke hoogte h kennen, kunnen we met een integraal de inhoud van viervlak ABCD berekenen.
5p 13. Bereken exact de inhoud van het viervlak ABCD

 
Osteoporose
Osteoporose of botontkalking is een kwaal die vooral bij oudere mensen optreedt en verergert naarmate men ouder wordt. Bij het ouder worden maakt het lichaam minder bot aan dan er afgebroken wordt. Het gevolg is dat botten poreuzer worden en de kans op botbreuk dus toeneemt.

In deze opgave beperken we ons tot de risicogroep, personen van 55 jaar en ouder. Onderzoek wijst uit dat 1 op de 4 vrouwen aan osteoporose lijdt.
Bij mannen is dat 1 op de 12.

Bij een controle op osteoporose onder 100 aselect gekozen vrouwen wordt bij een aantal vrouwen osteoporose geconstateerd. 

3p 14. Bereken de kans dat dit aantal 30 is.

 
Bij een controle onder vijf aselect gekozen mannen en vijf aselect gekozen vrouwen wordt bij een aantal van hen osteoporose geconstateerd.
7p 15. Bereken de kans dat dit aantal 2 is.

 
In 1988 bestond in Nederland de risicogroep voor 55,6% uit vrouwen.
4p 16. Bereken hoeveel procent van de osteoporose-patiënten uit de risicogroep vrouw was.

 
Kogelbanen
Vanuit een bepaald punt worden kogels afgeschoten met steeds dezelfde beginsnelheid. De hoek waaronder men de kogels afschiet varieert. Zie de figuur hiernaast.

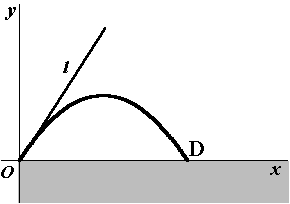
We brengen een assenstelsel aan in het vlak van de kogelbaan, met de x-as horizontaal en de y-as verticaal. De kogels worden afgeschoten in het punt (0,0) en komen neer in een punt D op de x-as. Zie de tweede figuur hiernaast. In deze figuur is behalve de kogelbaan ook de raaklijn l in (0,0) aan deze baan getekend. De kogel wordt weggeschoten in de richting van l.

Uit de mechanica is bekend dat een kogelbaan een deel van een paraboolbaan is.
Een vergelijking van de kogelbaan is:

y = r x - (0,1 + 0,1r2)x2

Hierbij is r een constante die afhangt van de hoek waaronder geschoten wordt.

De richtingscoëfficiënt van l is gelijk aan r.


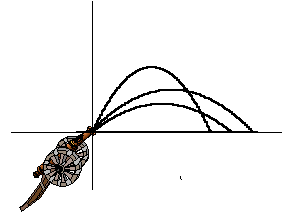4p 17. Toon dit aan.

 
Er geldt:  OD = 10r/(1 + r2)
4p 18. Toon dit aan.

 
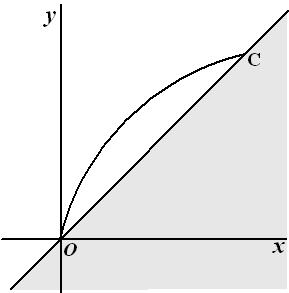Veronderstel dat de kogel niet op een horizontaal terrein wordt afgeschoten, maar op een hellend terrein met richtingscoëfficiënt 1. Zie de figuur hiernaast. Het hangt van r af waar de kogel op het terrein neerkomt. Dit punt noemen we C.

De x - coördinaat van punt C is 

4p 20. Bereken de maximale lengte van OC in twee decimalen nauwkeurig.

 
OPLOSSINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. Voor één willekeurig gekozen man is de kans NORMALCDF(-1E99 , 200 , 180 , 12.8) = 0,9409
Voor vier mannen wordt de kans dan  0,94094 = 0,7838
2. Dan moet gelden  NORMALCDF(177, 1E99 , 167, X) = 0,278
Invoeren in de GR en met INTERSECT oplossen levert X = 17 dus de standaardafwijking is 17
3. 100 • e0,1(18 - 40) = 100 • e-0,2(t - 100) ⇒  0,1(18 - 40) = -0,2(t - 100)
⇒  -2,2 = -0,2t + 20 
⇒  0,2t = 22,2
 ⇒ t = 111
4. De primitieve van z'(t) is  z(t) = 100•e0,1(t - 40) • (1/0,1) + c  =  1000 • e0,1(t - 40) + c
Daaraan is te zien dat moet gelden  a = 1000 en dat de constante gelijk moet zijn aan b.
t = 0 invullen geeft dan  z(0) = 1000 • e 0,1•-40 + b = 18,3156... + b = 30
Daaruit volgt  b= 30 - 18,3156... = 11,6843... Dus b ≈ 11,68
5.
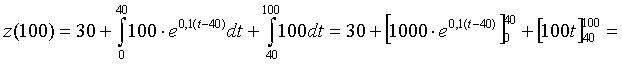= 30 + 1000•e0 - 1000•e-0,1•40 + 100•100 - 100•40 = 30 + 1000 -  18,31...+ 10000 - 4000 = 7011,68
6.
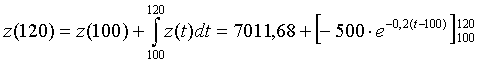
= 7011,68 - 500 • e -4 + 500•e0 = 7011,68 - 9,16 + 500 ≈ 7503
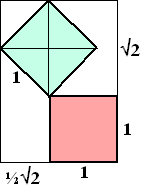
7. De situatie is dan als hiernaast.
De diagonaal van een vierkant met zijde 1 heeft lengte √2
De rechthoek er omheen heeft dan afmetingen  1 + √2  bij  0,5√2 + 1
De omtrek is  (1 + √2)(0,5√2 +1) = 0,5√2 + 1 + 1 + √2 = 2 + 1,5√2
8. In de figuur hiernaast zijn een aantal hulplijnen getrokken.
Daardoor ontstaan drie kleine rechthoekige driehoekjes, waarin we SOS-CAS-TOA mogen toepassen.
cos t = a/1 geeft  a = cos t
sin t = b/1  geeft  b = sin t
 sin t = c/1  geeft  c = sin t
De hoogte van de rechthoek is  1 + a + b, de breedte is  1 + c
De oppervlakte is dan  (1 + a + b) • (1 + c) =
= (1 + cos t + sin t) • (1 + sin t)
En dat is precies de gezochte formule.
9. De figuur hiernaast is op verschillende manieren te verkrijgen:

Spiegelen in de diagonaal van het vierkant.

of

De lengte en breedte van de omschrijvende rechthoek verwisselen.
10. R'(t) = cost • (1 + cos t + sin t) + (1 + sin t) • (cos t - sin t )
R'(0) = cos0 • (1 + cos 0 + sin 0) + (1 + sin 0)(cos 0 - sin 0) = 1 • (1 + 1 + 0) + (1 + 0)(1 - 0) = 2 + 1 = 3
11. In driehoek ABF geldt  SR = h , dus  SF = 8 - h (want  FR = 8)
Driehoek FPQ is gelijkvormig met driehoek FAB
Daarom geldt   FS/PQ = FR/AB  ⇒  (8- h)/PQ = 8/10
Dus  8 • PQ = 10 • (8 - h) = 80 - 10h ⇒  PQ = 10 - 10/8 • h = 10 - 5/4h 
12. De oppervlakte van een rechthoek op hoogte h is  (10 - 5/4h) • 3/4h = 7,5h - 15/16h2
De oppervlakte is maximaal als de afgeleide nul is:  7,5 - 30/16h = 0  ⇒  h =  4.
h = 4 geeft  voor de ene zijde 10 - 5/4h = 5 en de andere zijde 3/4 • 4 = 3
Die zijn ongelijk dus het is geen vierkant.
   
13.
   
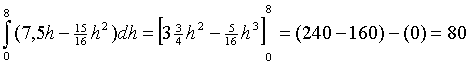
14. Dit is een binomiaal experiment met n = 100,  p = 0,25
P(X = 30) = binompdf(100, 0.25, 30) = 0,04575...

of:  0,2530 • 0,7570 • (100 nCr 30) = 0,04575...
   
15. Er zijn drie mogelijkheden:
2 mannen en 0 vrouwen:  P = binompdf(5,1/12,2) • binompdf(5,0.25,0) = 0,0127
1 man en 1 vrouw:  P = binompdf(5,1/12,1) • binompdf(5,0.25,1) = 0,1164
0 mannen en 2 vrouwen:  P = binompdf(5,1/12,0) • binompdf(5,0.25,2) = 0,1707
Samen geeft dat  0,0127 + 0,1164 + 0,1707 ≈ 0,3
   
16. Kies bijvoorbeeld een groep van 100000 mensen.
Dat zijn dan  55600 vrouwen en 44400 mannen   (55,6% en 44,4%)
Dat geeft  13900 vrouwen met osteoporose en 41700 zonder  (1/4 en 3/4)
Verder geeft het  3700 mannen met osteoporose en  40700 zonder (1/12 en 11/12)
De osteoporose patiënten zijn dus 13900 vrouwen en 3700 mannen; in totaal 17600.
Het percentage vrouw is  13900/17600 • 100% = 79%
   
17. y' = r - 2 • (0,1 + 0,1r2) • x
dus y'(0) = r
   
18. y = 0  geeft  x • {r - (0,1 + 0,1r2)x) = 0  ⇒  x = 0  ∨  r  - (0,1 + 0,1r2)x = 0
De eerste is de oorsprong en de tweede geeft:  r = (0,1 + 0,1r2)x ⇒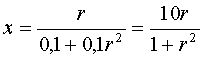
   
19. Dan is de afgeleide nul (met de quotiëntregel):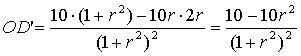

Dat is nul als  10 - 10r2 = 0  ⇒  r2 = 1  ⇒  r = 1  (of r = -1 maar die kan niet)
   
20. Dan is weer de afgeleide nul: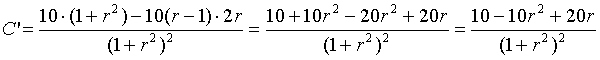

dat is nul als  -10r2 + 20r + 10 = 0
De ABC-formule geeft  r = -0,41  ∨  r = 2,41
De juiste waarde is r = 2,41  en dat geeft een lengte van  C = 3,41