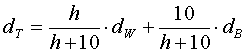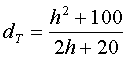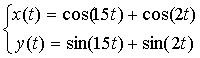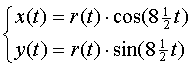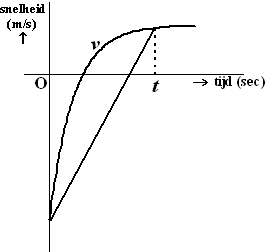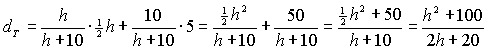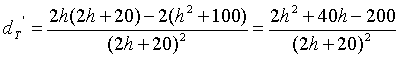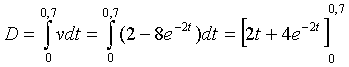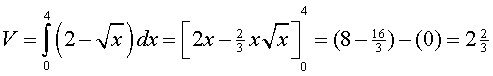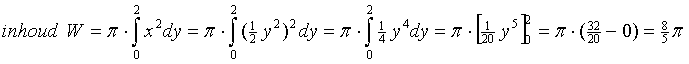VWO WB1,  2002 - I
Verschuivend zwaartepunt.
Een kubusvormige bak met deksel heeft binnenmaten 10 bij 10 bij 10 en weegt 1 kilogram.
Het zwaartepunt B van de bak ligt in het centrum van de bak, dus 5 cm boven het midden van de bodem.

De bak wordt met water gevuld tot een hoogte h cm.
Het zwaartepunt W van het water (de bak niet meegerekend) ligt in het centrum van het water, dus 0,5h cm boven het midden van de bodem.
In de figuur hiernaast is een vooraanzicht van de bak getekend.

Het zwaartepunt van het geheel (bak en water) noemen we T.
Het punt T ligt op het lijnstuk BW.
Er blijkt te gelden:



Hierbij zijn dT, dW en dB de afstand in cm van achtereenvolgens T, W en B tot de bodem.

3p 1. Bereken dT voor h = 3. Geef je antwoord in één decimaal nauwkeurig.

  
4p 2. Toon aan dat voor de afstand van T tot de bodem, uitgedrukt in h geldt:
Als de bak leeg is valt T samen met B. Tijdens het vullen van de bak verschuift de plaats van T eerst omlaag en later weer omhoog. Als de bak vol is valt T weer samen met B.

 
4p 3. Bereken voor welke waarden van h geldt: dT < 4,5. Geef je antwoord in één decimaal nauwkeurig.

 
6p 4. Bereken exact voor welke waarde van h de afstand van T tot de bodem minimaal is.

 
Pestgedrag
Om meer te weten te komen over het pestgedrag op een school wordt er een onderzoek gedaan. Aan elke leerling die aan het onderzoek meedoet wordt de volgende vraag gesteld: pest jij wel eens? Omdat het onderwerp gevoelig ligt zal niet elke pester naar waarheid willen antwoorden.
Daarom laat men de leerlingen antwoorden volgens de methode van randomized response . Deze methode werkt als volgt: er wordt gebruik gemaakt van een kansschijf die verdeeld is in de sectoren ja (15%), nee (15%) en naar waarheid (70%). Zie de figuur hiernaast.
De leerling laat de kansschijf langs de wijzer draaien. Hij komt tot stilstand in een willekeurige positie. Als de wijzer bij de sector naar waarheid staat moet de leerling eerlijk antwoorden. Als de wijzer bij één van de andere sectoren staat moet de leerling verplicht antwoorden wat die sector aangeeft, omgeacht of hij wel of niet pest.
4p 5. Bereken de kans dat van 7 leerlingen er 5 naar waarheid moeten antwoorden en 2 verplicht met "ja". Geef je antwoord in drie decimalen nauwkeurig.

  
Leerlingen die het antwoord "ja" geven doen dat om één van de volgende redenen:
  • de wijzer komt in de sector "ja" dus ze antwoorden verplicht "ja"
  • de wijzer komt in de sector "naar waarheid" en ze pesten wel eens.
Aan het onderzoek doen 900 leerlingen mee.
Neem bij de volgende vraag aan dat 20% van deze leerlingen wel eens pest.
4p 6. Toon aan dat dan naar verwachting 261 leerlingen "ja" zullen antwoorden..

 
Bij de telling blijkt dat 311 leerlingen de vraag met "ja" hebben beantwoord. Dit doet vermoeden dat het percentage leerlingen dat wel eens pest groter is dan 20%.
5p 7. Bereken bij welk percentage leerlingen dat wel een pest het verwachte aantal antwoorden "ja" 311 is.

 
Een beweging door (0,0)
De beweging van een punt in het Oxy vlak wordt voor  0 ≤ t ≤ 2π gegeven door:

In de figuur hiernaast is de baan van het punt getekend.
6p 8. Bereken de exacte snelheid van het punt op het tijdstip t = 0

 
De bewegingsvergelijkingen kunnen herleid worden tot:

met  r(t) = 2 • cos(6,5t)
4p 9. Toon dit aan.

 
Bij het doorlopen van de baan van de figuur hierboven voor  0 ≤ t ≤ 2π passeert het punt een aantal keren (0,0).
6p 10. Bereken dit aantal langs algebraïsche weg.

 
Hoogwater in Groningen
Op 26 oktober 1999 verscheen in het dagblad Trouw een artikel over de waterhoogte in het Verbindingskanaal in Groningen. De aanleiding hiervoor was de waterschade aan het Groninger Museum, dat in dit kanaal staat.
De grafiek hiernaast is ontleend aan dit artikel. Het is de frequentieverdeling van de meetresultaten van 8145 dagen in de jaren 1977 - 1999.

De waterhoogte (in cm boven NAP) in het Verbindingskanaal noemen we X. Op basis van de meetresultaten veronderstellen we dat X normaal verdeeld is met gemiddelde 63,8 cm. Van de 8145 gemeten waterhoogten was 6% onder de 50,0 cm. Hieruit volgt dat de standaardafwijking van X ongeveer 9 cm is.
4p 11. Bereken op grond van bovenstaande gegevens de standaardafwijking van X in één decimaal nauwkeurig.

 
Uit de statistiek is bekend dat het gemiddelde van een steekproef uit deze meetresultaten ook normaal verdeeld is met μ = 63,8 en σ = 9/√n, waarbij n het aantal meetresultaten in de steekproef is.
Lettend op de neerslag en de verdamping is december de natste maand in Groningen. Om te onderzoeken of de waterhoogte in december significant hoger is dan 63,8 berekent men het gemiddelde G van de 22 waterhoogtes op 15 december van de jaren 1977 tot en met 1998.
7p 12. Bereken bij welke gehele waarden van G men bij een significantieniveau van 5% mag concluderen dat de gemiddelde waterhoogte in december groter is dan 63,8.

 
Bal te water
Een bal valt van enige hoogte in het water. Vanaf het moment dat de bal het wateroppervlak raakt wordt hij afgeremd. Door zijn snelheid zal hij nog een stuk onder het wateroppervlak komen. Vervolgens zal de bal weer opstijgen naar het wateroppervlak. Zie de figuur hiernaast.
Voor de snelheid v, in meters per seconde, van een bepaalde bal die in het water valt geldt de formule:

v(t) = 2 - 8 • e-2t

Hierbij is t de tijd in seconden vanaf het moment dat de bal in het water komt; v is positief als de bal omhoog gaat.
Deze formule geldt alleen zolang de bal onder water is. 
Ter vereenvoudiging verwaarlozen we de diameter van de bal.

 
In de onderste figuur hiernaast staat de grafiek van v voor de periode dat de bal onder water is.
De gemiddelde versnelling (in m/s2) van de bal tijdens de eerste t seconden dat hij onder water is, is gelijk aan de helling van het verbindingslijnstuk tussen de punten op de grafiek van v die horen bij de tijdstippen 0 en t. In de figuur is dit lijnstuk voor een waarde van t getekend.
4p 13. Bereken de gemiddelde versnelling in m/s2 gedurende de eerste 2 seconden. Geef je antwoord in twee decimalen nauwkeurig.

 
De bal bereikt het diepste punt na ongeveer 0,7 seconden.
5p 14. Bereken het exacte tijdstip waarop de bal op het diepste punt is.

 
Het aantal meters dat de bal zich op een bepaald tijdstip onder water bevindt kun je berekenen door de snelheid te integreren.
4p 15. Bereken de grootste diepte die de bal bereikt. Geef je antwoord in centimeters nauwkeurig.

 
Een kromme van middens
Gegeven is de functie  f(x) = √x
De lijn y = 2 snijdt de grafiek van f  in punt A en de y-as in punt B. Zie de figuur hiernaast. V is het gebied ingesloten door de grafiek van f, de y-as en de lijn y = 2. In de figuur is V grijs gemaakt.
4p 16. Bereken de oppervlakte van V

 
We bekijken het horizontale verbindingslijnstuk tussen een punt (0, q) en de grafiek van f  met  0 < q ≤ 2
M is het midden van dit lijnstuk. In de figuur hiernaast is dit voor een waarde van q getekend. Hierin is ook de kromme  y = √(2x) getekend.
4p 17. Toon aan dat M op de grafiek van  
y = √(2x) ligt.

 
W is het gebied dat wordt ingesloten door de grafiek van y = √(2x), de y-as en de lijn y = 2.
We wentelen V en W beide om de y-as.
De inhoud van het omwentelingslichaam van V is gelijk aan  32π/5. De inhoud van het omwentelingslichaam van W is een percentage hiervan.
6p 18. Bereken dit percentage exact.

 
OPLOSSINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
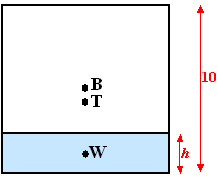
1. dW = 0,3 • 3  = 1,5.
dT = (3/13) • 1,5 + (10/13) • 5 = 4,5 cm.
2. dW = 0,5h geeft:
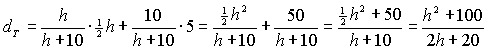
3. 1e opl. (h2 + 100) / (2h + 20) = 4,5  ⇒  h2 + 100 = (2h + 20) • 4,5  ⇒ h2 + 100 = 9h  + 90
 ⇒  h2 - 9h + 10 = 0   en de ABC-formule geeft nu  h = 7,7  of  h = 1,3
Aflezen uit de grafiek of met een tekenbeeld:   dT < 4,5 als  1,3 < h < 7,7
2e opl. Voer de formule voor dT in in de GR bij Y1. Neem Y2 = 4,5 en gebruik INTERSECT om de snijpunten te vinden. Dat geeft x = 7,7 of  x = 1,3. Aflezen uit de grafiek geeft dT < 4,5 als  1,3 < h < 7,7
4. Gebruik de quotiëntregel om de afgeleide functie van dT te vinden:

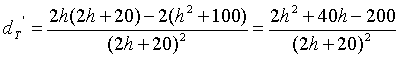
Dit is nul als de teller nul is:  2h2 + 40h- 200 = 0  geeft  met de ABC-formule  h = -10 + √200  of  h = -10 - Ö200
De tweede oplossing valt af, want geeft negatieve h. Dus de oplossing is  h = -10 + √200
5. Een mogelijke serie is  WWWWWJJ en de kans hierop is  0,75 • 0,152
Er zijn  7 nCr 2 zulke series. Dat is 21.
De totale kans wordt dan 21 • 0,75 • 0,152 = 0,079
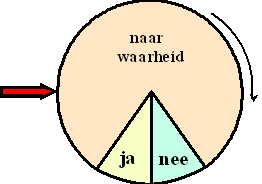
6. Naar verwachting zullen 0,25 • 900 = 135 leerlingenverplicht "ja"  antwoorden.
Naar verwachting zullen  0,7 • 0,2 • 900 = 126 leerlingen naar waarheid "ja" antwoorden
In totaal zullen dus  135 + 126 = 261 leerlingen "ja" antwoorden.
7. Van de 900 leerlingen hebben er naar verwachting 0,15 • 900 = 135 verplicht "ja" geantwoord.
Dus hebben er  311 - 135 = 176 naar waarheid "ja" geantwoord.
In totaal hebben er 0,70 • 900 = 630 leerlingen naar waarheid geantwoord.
Van die 630 zeiden er 176 "ja"  dus dat is  (176/630) • 100% = 28%.
8. x ' (t) = -15sin(15t)- 2sin(2t) dus x'(0) = 0
y'(t) = 15cos(15t) + 2cos(2t) dus y '(0) = 17
De snelheid is √(x'2 + y'2) = √172 = 17
9.
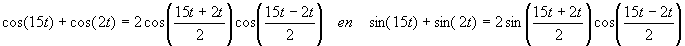
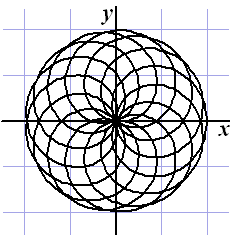
dus  x(t) = 2cos(8,5t)cos(6,5t)  en  y(t) = 2sin(8,5t)cos(6,5t)
Neem r(t) = 2cos(6,5t) dan staat er  x(t) = r(t)•cos(8,5t)  en   y(t) = r(t)•sin(8,5t)
10. In de oorsprong is x(t) = 0  en y(t) = 0
Dat kan alleen als r(t) = 0, want cos(8,5t) en sin(8,5t) kunnen nooit tegelijk nul zijn
cos(6,5t) = 0  geeft  6,5t = 0,5π + k • π
dat geeft  t  = (1/13)π + k •  (2/13)π
tussen 0 en 2p  geeft dat de oplossingen  (1/13)π, (3/13)π, (5/13)π, ... , (25/13)π, en dat zijn er 13.
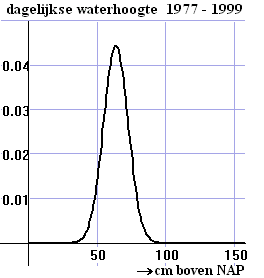
11. NORMALCDF(-1E99 , 50.0 , 63.8 , X) = 0,06
Plot Y1 = NORMALCDF(-1E99 , 50.0 , 63.8 , X)  en Y2 = 0,06
bijv met WINDOW Xmin = 5 , Xmax = 10 , Ymin = 0, Ymax = 0,12
INTERSECT geeft X = 8,87588.... dus s = 8,9
12. H0: G is normaal verdeeld met  μ = 63,8 en σ = 9/√22 = 1,92
De toets is eenzijdig, dus H0 wordt verworpen als geldt:  P(G > g) £ 0,05
Dus NORMALCDF(X , 1E99 , 63.8 , 1.92) £ 0,05
Plot Y1 = NORMALCDF(X , 1E99 , 63.8 , 1.92) en Y2 = 0,05
bijv. met WINDOW  Xmin = 60 , Xmax = 80 , Ymin = 0, Ymax = 0,10
INTERSECT geeft X = 66,7936.... dus voor gehele waarden die groter of gelijk zijn aan 67.
13. gemiddelde versnelling = (v(2) - v(0) )/2 = 3,93
14. 2 - 8e-2t = 0 ⇒ 8e-2t = 2  ⇒  e-2t = 0,25  ⇒  -2t = ln0,25  ⇒  t = -0,5 • ln(0,25)  = ln2
15.
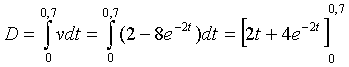
= 2 • 0,7 + 4 • e-1,4 - 0 - 4 • e0 = -1,61361...
De grootste diepte is dus 1,61 meter.
(de integraal mag overigens ook opgelost worden  met CALC - ∫f(x)dx van de GR)
16.
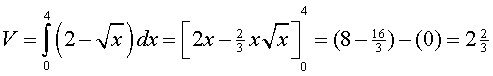
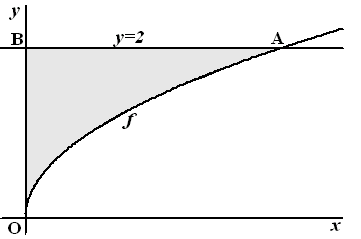
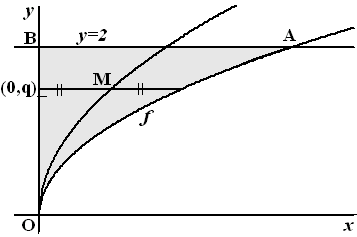
17. 1e opl. Het rechter eindpunt van het verbindingslijnstuk is (q2 , q)
Dus M is (0,5q2 , q)
 √(2 • 0,5q2) = √(q2) = q dus M ligt inderdaad op de tweede grafiek.
2e opl. De grafiek van de middens ontstaat uit de oorspronkelijke grafiek door een vermenigvuldiging t.o.v. de y-as met factor 0,5.
Dat is hetzelfde als in de formule x vervangen door 2x
18.
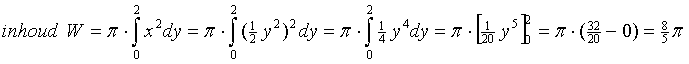
dat is dus 20% van de inhoud van V.