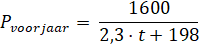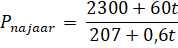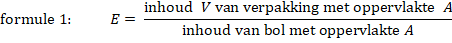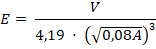| Goudplevieren. | |||
|
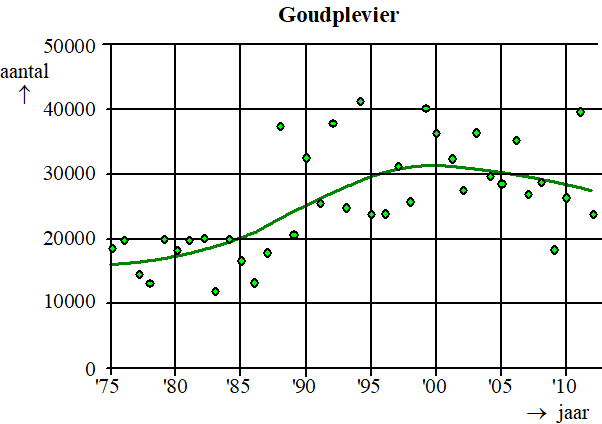
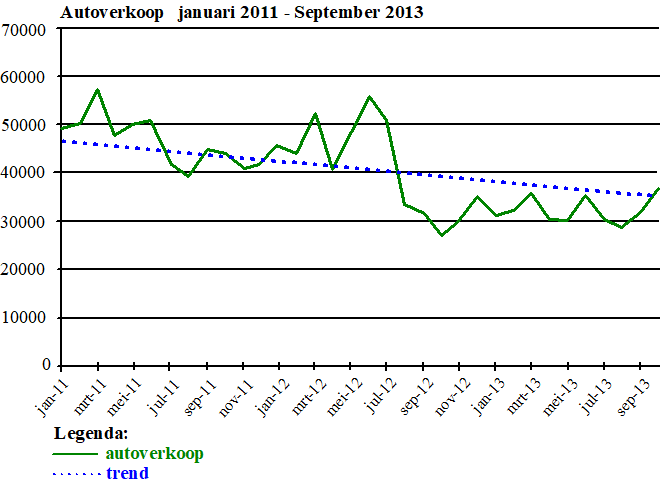
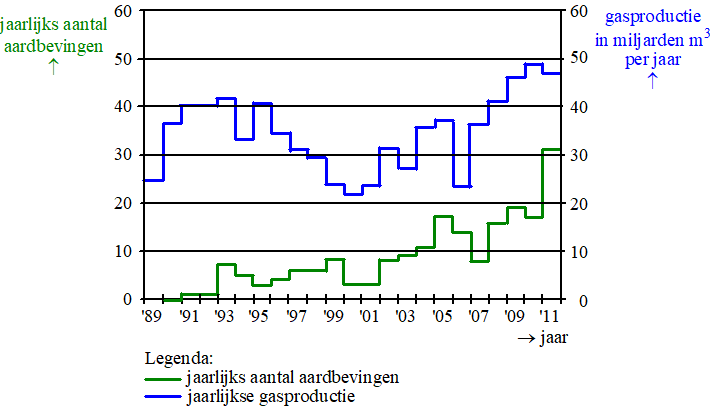
Een goudplevier (zie foto) is een vogel die niet in Nederland broedt, maar tijdens zijn trektochten wel in Nederland te vinden is. Er zijn grote verschillen in aantallen goudplevieren tussen de verschillende jaren. In onderstaande figuur zijn de aantallen goudplevieren in Nederland in de jaren 1975 tot en met 2012 weergegeven als groene stippen. |
 |
||
|
|
|||
|
In deze figuur is ook een kromme getekend die de trend aangeeft. We nemen aan dat vanaf 2003 deze trend een rechte lijn is en dat dit ook na 2012 zo blijft. |
|||
|
4p. |
1. |
Bereken hoeveel goudplevieren er volgens de trendlijn zijn in 2020. Geef je antwoord in gehele duizendtallen. |
|
|
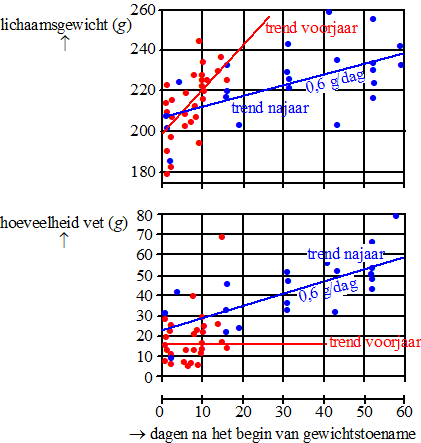
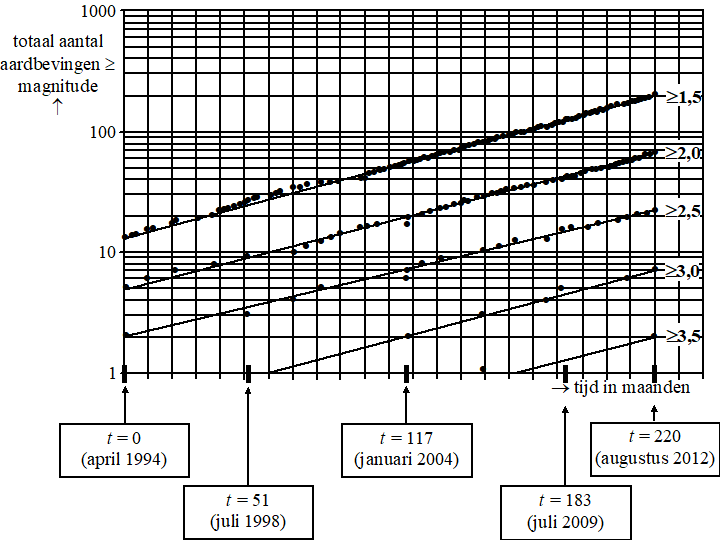
Tijdens hun verblijf in Nederland bouwen de goudplevieren een reserve op voor de komende trektochten. Hierdoor nemen ze toe in gewicht. In onderstaande figuur zie je het resultaat van een onderzoek naar deze gewichtstoename: van een aantal op verschillende tijdstippen gevangen goudplevieren is het gewicht en/of de hoeveelheid vet bepaald. De open stippen horen bij waarnemingen in het najaar en de dichte stippen bij waarnemingen in het voorjaar. Ook zijn de trendlijnen getekend. |
|||
|
|
|||
|
Op grond van specifieke biologische kenmerken kunnen de
onderzoekers bepalen wanneer de gewichtstoename van een goudplevier
begint. |
|||
| I |
In het voorjaar is de gemiddelde gewichtstoename per dag van een goudplevier ongeveer 2 keer zo groot als in het najaar. |
||
| II | De gewichtstoename in het voorjaar bestaat niet uit vet. | ||
|
4p. |
2. |
Onderzoek voor elk van beide stellingen of deze waar is. | |
|
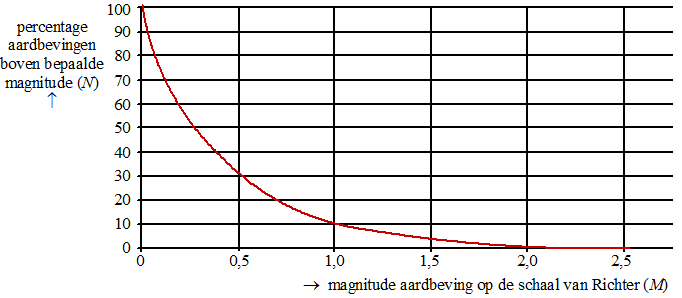
Het vetpercentage van een vogel is de hoeveelheid lichaamsvet als percentage van het totale gewicht van de vogel. Met behulp van de trendlijnen in het voorjaar van zowel lichaamsgewicht als vethoeveelheid leiden de onderzoekers het volgende verband af: |
|||
|
|
|||
|
Hierbij is Pvoorjaar het vetpercentage van de vogel in het voorjaar en t de tijd in dagen na het begin van de gewichtstoename. |
|||
|
5p. |
3. |
Laat zien, gebruikmakend van de punten (0, 198) en (20, 244), hoe deze formule is af te leiden uit de gegevens in de figuur. |
|
|
3p. |
4. |
Beredeneer uitsluitend met behulp van de formule, zonder getallen in te vullen of een schets te maken, of het vetpercentage in het voorjaar toeneemt of juist afneemt. |
|
|
Voor het vetpercentage in het najaar gaan we uit van de volgende formule: |
|||
|
|
|||
|
Hierin is Pnajaar het vetpercentage van de vogel in het najaar en t de tijd in dagen na het begin van de gewichtstoename.Met behulp van de afgeleide van Pnajaar kan men onderzoeken of het vetpercentage Pnajaar afnemend stijgend is. |
|||
|
6p. |
5. |
Stel de formule van de afgeleide van Pnajaar op en onderzoek daarmee of Pnajaar afnemend stijgend is. |
|