Nieuwe pagina 1

KNAB.

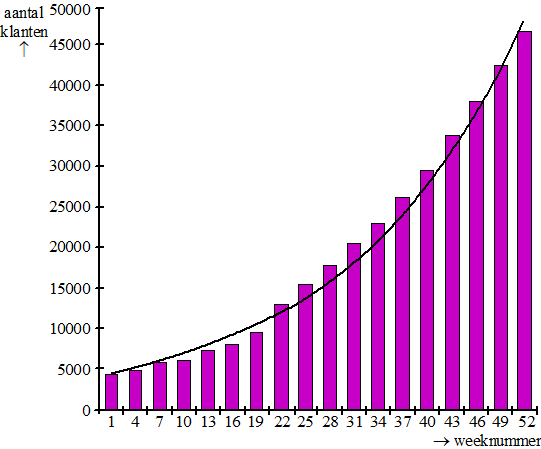
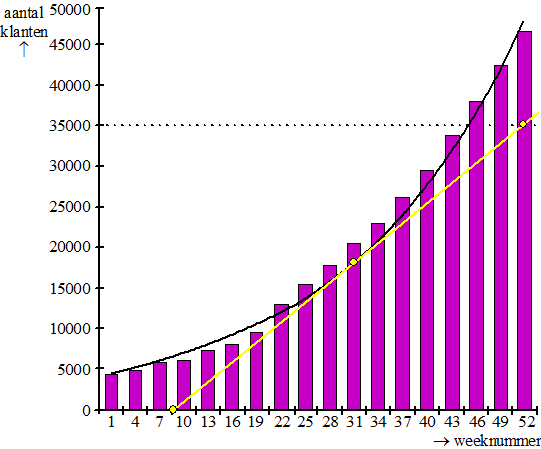
Knab is een tamelijk nieuwe bank, gestart in 2012 als onderdeel van Aegon. In het begin groeide Knab maar langzaam: eind 2013 had de bank nog maar 4500 klanten. Daarom besloot de bank in 2014 de zaken anders aan te pakken. Dit leverde direct resultaat op, want het aantal klanten is in 2014 tien keer zo groot geworden. Zie de figuur.



In de figuur zijn door middel van staven de aantallen klanten om de drie weken weergegeven. Bovendien is de grafiek getekend van een exponentieel model dat de werkelijke aantallen goed benadert. Het exponentiële model wordt gegeven door de formule: N = 4500 • e^{0,0463 •}^t Hierin is t de tijd in weken sinds het begin van 2014 met t = 0 in week 1 en N het aantal klanten. In week 43 lijkt het verschil tussen het aantal klanten volgens het model en het werkelijke aantal klanten het grootst.

3p.	1.	Bereken dit verschil in week 43. Rond je antwoord af op honderdtallen.

Zoals gezegd is het aantal klanten in het jaar 2014 vertienvoudigd. Dat lijkt inderdaad precies een jaar geduurd te hebben.

3p.	2.	Bereken met behulp van de formule het gehele aantal weken dat in het model nodig is voor een vertienvoudiging.

De snelheid waarmee het aantal klanten per week groeit, kun je benaderen door de helling van de grafiek op het betreffende tijdstip te bepalen.

4p.	3.	Benader met behulp van de grafiek in de figuur de snelheid waarmee het aantal klanten per week groeit in week 31 van 2014. Rond je antwoord af op honderdtallen.

Je kunt de formule N = 4500 • e^0,0463•^t zó herschrijven, dat bij een gegeven aantal klanten berekend wordt in welke week dat aantal bereikt wordt. Dat verband is van de vorm: t = a • ln(b • N)

3p.	4.	Bereken a en b. Rond de waarde van a af op twee decimalen en de waarde van b op vijf decimalen.

Blikstapelingen.

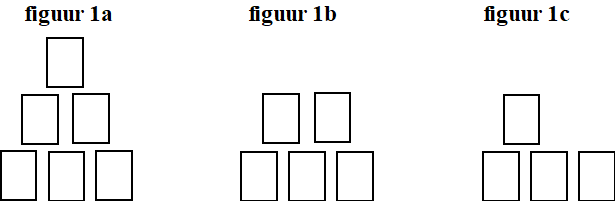
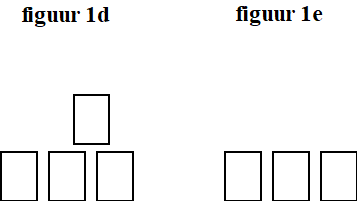
Bij het spel blikgooien krijgt de speler één of meer ballen waarmee hij of zij moet proberen zoveel mogelijk blikken van een toren af te gooien. Zo’n toren is altijd op dezelfde manier opgebouwd: op de onderste laag staat een aantal blikken en op de lagen erboven steeds één minder. Op de foto zie je een toren met zes blikken. We nemen in deze opgave aan dat, als een bal de toren raakt, de onderste laag in zijn geheel blijft staan. Neem aan dat een geraakt blik ook werkelijk van de toren afvalt en nooit “mooi” op een lager gelegen laag terechtkomt en ook dat blikken niet blijven staan als één of meer blikken eronder wegvallen. Lars gooit één bal naar een toren met zes blikken, zoals op de foto. Na zijn worp blijft de onderste laag van drie blikken staan. Er zijn nu vijf mogelijkheden voor de overgebleven toren. Drie van deze mogelijkheden zijn in figuur 1a, 1b en 1c schematisch getekend.



2p.	5.	Teken de andere twee mogelijkheden.

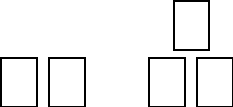
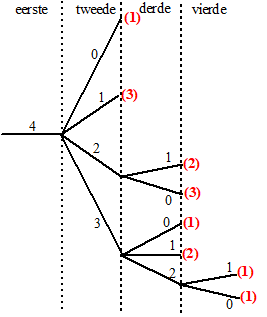
We gaan in deze opgave deze situatie wat theoretischer bekijken. We tellen het aantal mogelijke stapelingen van blikken op een onderste laag van n blikken. Hierbij staat vanaf de tweede laag ieder blik steeds boven op twee onderliggende blikken. We nemen steeds aan dat er één keer gegooid is en dat de hele onderste laag is blijven staan. Voor n = 1 is er maar één blik, dus is er ook één mogelijke stapeling. Voor n = 2 zijn er twee mogelijke stapelingen. Zie de volgende figuur.



Je kunt nu met een redenering nagaan dat het aantal mogelijke stapelingen voor n = 3 gelijk is aan 5. Deze redenering gaat als volgt:
-	Er is één manier met 3 blikken op de onderste laag en 0 blikken op de tweede laag.
-	Er zijn twee manieren met 3 blikken op de onderste laag en 1 blik op de tweede laag.
-	Er is één manier met 3 blikken op de onderste laag en 2 blikken op de tweede laag (figuur 1b).
-	Er is één manier met 3 blikken op de onderste laag, 2 blikken op de tweede laag en 1 blik op de derde laag (figuur 1a).
Dat is samen 1 + 2 + 1 + 1 = 5 mogelijkheden. Voor n = 4 is het aantal mogelijke stapelingen gelijk aan 14.

4p.	6.	Toon dit aan.

De Belgische wiskundige Charles Catalan ontdekte in de 19e eeuw de volgende formule: C_n = C₀ • C_n_-₁ + C₁ • C_n_-₂ + C₂ • C_n_-₃ +...+ C_n_-₂ • C₁ + C_n_-₁ • C₀ met C₀ =1 Hierin is C_n het aantal mogelijke stapelingen met n blikken op de onderste laag.

3p.	7.	Bereken met behulp van bovenstaande formule C₅.

Voor deze rij getallen, de zogenaamde Catalan-getallen, bestaat geen directe formule. Wel bestaat er een formule die voor grote waarden van n de Catalan-getallen benadert. Deze formule is B_n = 0,564 • e^{1,386 • n} • n^-1,5waarbij B_n een benadering is van het n^e Catalan-getal (C_n ). De getallen voor B_n worden snel groter. Hoe snel dit gaat, is te berekenen met behulp van de afgeleide van B_n. Er geldt (bij benadering): B_n' = 0,782 • e^{1,386 • n} • n^-1,5 - 0,846 • e^{1,386 • n} • n^-2,5

4p.	8.	Toon dit aan.

Vanaf een bepaald aantal blikken zal het aantal mogelijke stapelingen met meer dan 500000 toenemen als de onderste laag met één blik toeneemt.

3p.	9.	Onderzoek met behulp van de afgeleide van B_n vanaf welk aantal blikken op de onderste laag dit is.

Kaarten schudden.

Na het schudden begint een kaartspel meestal met het gelijk verdelen van de kaarten onder een aantal spelers. Neem aan dat bij een bepaald spel 16 verschillende kaarten gelijk verdeeld worden onder vier spelers A, B, C en D. Spelers A, B, C en D krijgen ieder dus vier kaarten. We bekijken een stapel kaarten bestaand uit 16 verschillende kaarten. Deze kaarten kunnen op circa 2,1 • 10¹³ verschillende volgordes liggen. Het aantal volgordes waarin de kaarten kunnen liggen, is veel groter dan het aantal mogelijkheden om de kaarten onder de vier spelers A, B, C en D te verdelen.

4p.	10.	Bereken hoeveel keer zo groot dit aantal is. Rond af op tienduizendtallen.

In 1992 publiceerden de Amerikaanse wiskundigen Bayer en Diaconis een artikel over het schudden van kaarten. Voor dit artikel hadden zij de meest gebruikte manier van schudden onderzocht, de zogeheten Riffle Shuffle (zie de foto). Zij kwamen tot de conclusie dat het met deze schudtechniek niet mogelijk is een stapel kaarten écht willekeurig te maken, zoals bijvoorbeeld een computer dat wel kan. Voor het spelen van een kaartspel is het goed genoeg als de kaarten “voldoende willekeurig” geschud zijn.
Bayer en Diaconis ontdekten tijdens hun onderzoek dat het aantal keren dat een stapel kaarten minstens geschud moet worden om als “voldoende willekeurig” bestempeld te worden, kan worden benaderd met de formule:

A = 1,5 • ²log(n)

In deze formule is A het aantal keren dat een stapel van n kaarten minstens geschud moet worden om als “voldoende willekeurig” bestempeld te worden. A wordt naar boven afgerond op een geheel getal. Het kaartspel jokeren wordt gespeeld met twee sets van 52 speelkaarten, aangevuld met in totaal 4 zogeheten jokers.

2p.	11.	Bereken hoe vaak de kaarten bij jokeren minstens geschud moeten worden volgens de formule van Bayer en Diaconis.

Als het aantal te schudden kaarten toeneemt, neemt ook het aantal keren dat er minstens geschud moet worden toe. Dit aantal neemt echter steeds langzamer toe. Je kunt dit zien aan de afgeleide ^dA/_dn

4p.	12.	Stel de formule op van de afgeleide ^dA/_d_n en beredeneer aan de hand van deze formule, dus zonder getallen in te vullen of een schets te maken, dat A afnemend stijgend is.

In de meeste casino’s kun je het spel blackjack spelen. Dat wordt over het algemeen gespeeld met vier spellen kaarten (totaal 208 kaarten). Het aantal keer dat zo’n groot aantal kaarten minstens geschud moet worden is helemaal niet zo groot: volgens de formule van Bayer en Diaconis slechts 12 keer. Dat is maar drie keer schudden meer dan bij één spel kaarten. Volgens de formule van Bayer en Diaconis geldt in het algemeen: als het aantal kaarten vier keer zo groot wordt, hoeft er maar drie keer extra geschud te worden.

4p.	13.	Toon dit aan met behulp van de formule voor A en de rekenregels voor logaritmen zonder gebruik te maken van getallenvoorbeelden.

Zeepbellen.

Op de foto zie je een dubbele zeepbel: twee bolvormige zeepbellen die aan elkaar vastzitten. Beide zeepbellen zijn een deel van een bol. Het scheidingsvlies tussen deze zeepbellen is ook een deel van een bol. Men heeft ontdekt dat voor elke dubbele zeepbel de volgende formule geldt: ¹/_c = ¹/_b - ¹/_a In deze formule is a de straal van de grootste zeepbel, b de straal van de kleinste zeepbel en c de straal van het bolvormige scheidingsvlies. In de figuur is dit schematisch weergegeven.



De dubbele zeepbel op de foto bestaat uit een zeepbel met een straal van 2,5 cm en een zeepbel met een straal van 4 cm.

3p.	14.	Bereken met behulp van bovenstaande formule de straal van het scheidingsvlies. Rond je antwoord af op hele millimeters.

Neem nu aan dat de grootste zeepbel een vaste straal heeft van 3 cm (dus a = 3). We vragen ons af wat er gebeurt als de straal van de kleinste zeepbel steeds kleiner wordt: wordt het scheidingsvlies dan steeds platter of steeds boller? Met andere woorden: neemt c toe of af?

4p.	15.	Beredeneer aan de hand van bovenstaande formule of c toeneemt of afneemt als de straal van de kleinste zeepbel steeds kleiner wordt.

Als de stralen a en b bekend zijn, kun je c snel en rechtstreeks berekenen door de formule ¹/_c = ¹/_b - ¹/_a te herleiden tot



3p.	16.	Geef deze herleiding.

Het antwoord op de vraag of het scheidingsvlies steeds platter of boller wordt als de kleinste zeepbel steeds kleiner wordt, kunnen we ook vinden met behulp van de afgeleide van c. We nemen opnieuw een grootste zeepbel met een vaste straal van 3 cm.


5p.	17.	Stel de afgeleide ^dc/_db van c = ^3b/_{(3 - b)} op en beredeneer aan de hand van de formule van deze afgeleide of c toeneemt of afneemt als de straal van de kleinste zeepbel kleiner wordt.

Schildpadden.

Sommige mensen hebben een schildpad als huisdier. Bepaalde soorten houden onder natuurlijke omstandigheden een winterslaap. De eigenaar kan ervoor kiezen om zijn schildpad ook in winterslaap te laten gaan, omdat hij anders de hele winter extra licht en warmte moet geven aan zijn huisdier. Een schildpad moet een gezond gewicht hebben bij het begin van zijn winterslaap, anders is er een kans dat hij het niet overleeft. Om vast te stellen of de schildpad een gezond gewicht heeft, wordt vaak de Jackson Ratio gebruikt. De Jackson Ratio R wordt berekend met de formule R = ^G/_L_³ Hierin is G het gewicht van de schildpad in gram en L de lengte van het schild van de schildpad in cm. Voor de Griekse landschildpad geldt de volgende vuistregel: een schildpad kan veilig aan een winterslaap beginnen als zijn Jackson Ratio tussen 0,18 en 0,22 ligt. Jesse heeft een Griekse landschildpad met een schildlengte van 15 cm en wil hem een winterslaap laten houden.

3p.	18.	Bereken in hele grammen nauwkeurig tussen welke waarden zijn gewicht dan mag liggen volgens de vuistregel.

De lengte van het schild moet recht gemeten worden, bijvoorbeeld door de schildpad met ingetrokken kop tussen een schuifmaat te zetten (zie foto 1). Veronderstel dat iemand toch de lengte over het schild heen meet (zie foto 2).



3p.	19.	Beredeneer of een schildpad door op die manier te meten een grotere of een kleinere Jackson Ratio krijgt dan hij in werkelijkheid heeft.

Op een Engelse website staat het volgende: als je het gewicht meet in Engelse ponden (lbs) en de schildlengte in inches, kun je de Jackson Ratio berekenen met de formule R = c • ^W/_l³ Hierin is W het gewicht in Engelse ponden en l de schildlengte in inches. 1 Engels pond (lb) ≈ 454 gram en 1 inch = 2,54 cm. De Jackson Ratio moet dan ook weer dezelfde waarde opleveren.

3p.	20.	Bereken de waarde van c in deze formule. Rond je antwoord af op één decimaal.

Een andere manier om te bepalen of een Griekse landschildpad veilig aan een winterslaap kan beginnen, is met behulp van de grafiek in onderstaande figuur. De grafiek geeft het gewicht van gezonde schildpadden als functie van de schildlengte. Als een schildpad met zijn lengte en gewicht in de buurt van deze grafiek zit, is het veilig om hem in winterslaap te laten gaan.



We vragen ons af of de grafiek van de figuur bij benadering overeenstemt met de eerder genoemde vuistregel. Om dit te onderzoeken kunnen we in de figuur de grafieken tekenen van de onder- en de bovengrens die horen bij de eerder genoemde vuistregel en vervolgens het gebied dat hoort bij die vuistregel in de figuur aangeven.

6p.	21.	Geef in de figuur het gebied aan waarin een schildpad zich volgens de vuistregel met zijn schildlengte en gewicht moet bevinden om veilig aan een winterslaap te kunnen beginnen.

Grotere windmolens.

Met behulp van windmolens wordt windenergie omgezet in elektriciteit. De afgelopen tientallen jaren zijn steeds grotere windmolens geplaatst, want hoe groter een windmolen, hoe groter de elektriciteitproductie door die windmolen. In deze opgave kijken we naar de toenemende opbrengst van windmolens bij toenemende grootte.

In de figuur zie je een schematische tekening van een windmolen met hierin aangegeven de ashoogte h en de ‘rotordiameter’ D. De maximale hoeveelheid elektriciteit die men met een windmolen kan produceren, noemt men het vermogen van de windmolen. Dit vermogen P wordt uitgedrukt in MW (megawatt). Het vermogen van een windmolen hangt onder andere af van de ashoogte. Doordat er op grotere hoogte meer wind is en doordat de wind daar constanter is, neemt het vermogen voor elke meter extra ashoogte met een bepaald percentage toe. Er geldt: bij gelijkblijvende rotordiameter neemt voor elke meter extra ashoogte het vermogen met 0,68% toe.
Het vermogen van een windmolen hangt naast de ashoogte ook af van de rotordiameter. Deze twee factoren spelen tegelijkertijd een rol. Dat komt tot uiting in de formule voor het vermogen:

P = 2,21 • 10^-4 • g^h • D²

Hierin is P het vermogen in MW, g de groeifactor per extra meter ashoogte, h de ashoogte in meter en D de rotordiameter in meter. In een windmolenpark staan 40 windmolens met elk een vermogen van 0,75 MW. De molens hebben een rotordiameter van 50 meter en een ashoogte van 45 meter. De windmolens in dit park zijn aan vervanging toe. Men wil deze windmolens vervangen door tien gelijke windmolens van een groter type. Men hanteert als vuistregel dat een windmolen van dit type € 25 000,- per meter ashoogte kost. Bij de huidige windmolens is de verhouding tussen ashoogte en rotordiameter gelijk aan ⁴⁵/₅₀ = 0,9 Deze verhouding zal ook gelden voor het grotere type windmolen, dus voor dit type geldt: h = 0,9D . Het totale vermogen van het park moet met de nieuwe windmolens minstens even groot worden als het met de huidige windmolens is.

7p.	22.	Bereken de minimale investering die gedaan zal moeten worden voor de bouw van de nieuwe windmolens. Rond je antwoord af op miljoenen euro’s.

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

1.	aflezen uit de figuur: een week 43 is het aantal ongeveer 34000 t = 0 in week 1, dus t = 42 in week 43. N = 4500 • e^{0,0463 • 42} = 31459 Dat scheelt 2500

2.	N = 4500 • e^{0,0463 •}^t t = 0 geeft de beginwaarde N = 4500 Als het moet vertiebvoudigen dan is de eindwaarde N = 45000 45000 = 4500 • e^{0,0463 •}^t e^{0,0463 •}^t = 10 0,0463t = ln10 t = ^ln(10)/_0,0463 = 49,73.... Dat is dus na 50 weken.

3.
	De raaklijn bij weeknummer 31 is getekend. Die gaat door bijv. (8.5, 0) en (52, 35000) De r.c. is dan ^{(35000 - 0)}/_{(52 - 8,5)} = 805 dat is ongeveer 800 klanten per week.

4.	N = 4500 • e^{0,0463 •}^t (¹/₄₅₀₀)N = e^{0,0463 •}^t ln( (¹/₄₅₀₀)N ) = 0,0463t t = (¹/_0,0463) • ln( (¹/₄₅₀₀)N ) t = 21,598... • ln(0,000222N) dus a = 21,60 en b = 0,00022

5.

6.	in onderstaand boomdiagram staan in het zwart de aantallen blikken op de lagen één, twee, drie en vier. In het rood staat het aantal manieren waarop die tak kan voorkomen.

	de rode getallen zijn 1 + 3 + 2 + 3 + 1 + 2 + 1 + 1 = 14

7.	C₅ = C₀C₄ + C₁C₃ + C₂C₂ + C₃C₁ + C₄C₀ = 1 • 14 + 1 • 5 + 1 • 1 + 5 • 1 + 14 • 1 = 42

8.	B_n = 0,564 • e^{1,386 • n} • n^-1,5 daar staat f • g met f = 0,564 • e^{1,386 • n} en g = n^-1,5 f ' = 0,564 • e^1,386n • 1,386 = 0,781704e^1,386n (met de kettingregel) g '= -1,5 • n^-2,5 gebruik de productregel: B ' = 0,782e^1,386n • n^-1,5+ 0,564 • e^{1,386 • n} • -1,5 • n^-2,5Dat geeft de gevraagde formule.

9.	de afgeleide moet gelijk zijn aan 500000 Y1 = 0,782 * e^(1,386X) • X^(-1,5)- 0,846 • e^(1,386 * X) • X^-2,5Y2 = 500000 Intersect geeft X = n = 12,439.... dat is dus vanaf 13 blikken.

10.	geef speler A 4 kaarten uit de 16: kan op 16 nCr 4 = 1820 manieren geef speler B 4 kaarten uit de resterende 12: kan op 12 nCr 4 = 495 manieren geef speler C 4 kaarten uit de resterende 8: kan op 8 nCr 4 = 70 manieren de laatste 4 zijn nu voor speler D in totaal 1820 • 495 • 70 • 1 = 63063000 manieren 2,1 • 10¹³ / _63063000= 333000,333... keer zo groot. Dat is ongeveer 330000 keer zo groot.

11.	A = 1,5 • ²log(108) = 1,5 • log(108)/log(2) = 10,13....... 11 keer schudden dus.

12.	^dA/_dn = 1,5 • ¹/_(nln2) n is positief, dus dA/dn ook (alles is positief) dus A stijgt als n groter wordt, dan wordt de noemer van A' groter, dus dan wordt A' zelf kleiner. Dus de stijging van A is afnemend.

13.	A = 1,5 • ²log(n) vervang nu n door 4n: A_nieuw= 1,5 • ²log(4n) = 1,5 • (²log4 + ²logn) = 1,5 • ²log4 + 1,5 • ²logn = 3 + 1,5 • ²logn = 3 + A_oud.Dus drie keer extra schudden.

14.	a = 4 en b = 2,5 invullen: ¹/_c = ¹/_2,5 - ¹/₄ ¹/_c = 0,15 c = ¹/_0,15 =6,666 cm = 67 mm

15.	¹/_c = ¹/_b - ¹/₃ Als b kleiner wordt, dan wordt ¹/_b groter Dan wordt ¹/_b - ¹/₃ ook groter dus wordt ¹/_c groter Maar dan wordt c dus kleiner. Als de straal van de kleinste zeepbel steeds kleiner wordt neemt c dus af.

16.

17.
	c ' is altijd positief (want de noemer is een kwadraat en dat is altijd positief, en de teller is ook een positief getal) Dat betekent dat de grafiek van c(b) altijd stijgt. Als b dus kleiner wordt, wordt c ook kleiner.

18.	^G/₁₅_³= 0,18 geeft G = 0,18 • 15³ = 607,5 ^G/₁₅_³= 0,22 geeft G = 0,22 • 15³ = 742,5 dus G moet liggen tussen 607 en 743

19.	Door deze manier van meten wordt L groter. G verandert niet, dus de noemer van R wordt groter terwijl de teller gelijk blijft. Dan wordt R kleiner. Dus de schildpad krijgt een kleinere Jackson Ratio

20.	G = 454W en L = 2,54l

	Dus c = 27,7

21.
	De grafiek G/L³ = 0,18 is dezelfde als G = 0,18L³ en dat is de onderste rode lijn in de figuur De grafiek G/L³ = 0,22 is dezelfde als G = 0,22L³ en dat is de bovenste rode lijn in de figuur Het bedoelde gebied is het gele gebied daartussen.

22.	Het totale vermogen van het windpark is 40 • 0,75 = 30 MW Er zijn 10 windmolens, dus een nieuwe windmolen moet een vermogen van (minstens) 3 (MW) hebben P = 2,21 • 10^-4 • g^h • D² g = 1,0068 dus P = 2,21 • 10^-4 • 1,0068^h • D² h = 0,9D dus P = 2,21 • 10^-4 • 1,0068^0,9D • D² P moet gelijk zijn aan 3. 3 = 2,21 • 10^-4 • 1,0068^0,9D • D² Y1 = 3 en Y2 = 2,21 • 10^-4 • 1,0068^(0,9X) • X² intersect levert X = D = 88,8....m De minimale ashoogte is h = 0,9 • 88,8... = 79,9...m dat kost 10 • 79,9... • 25000 = 19992347,... dus de gevraagde investering is 20 miljoen euro

VWO WA, 2018 - II