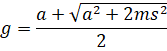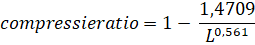VWO WA, 2018 - I     Bezem

 

Bedreigde vogels.
       

In Nederland worden veel soorten weidevogels in hun bestaan bedreigd. In de figuur staat een grafiek van de ontwikkeling van de aantallen broedende grutto-paren sinds 1964.

Bij deze grafiek heeft men gebruik gemaakt van indexcijfers: men kiest een basisjaar en geeft de aantallen broedende grutto-paren in elk ander jaar als percentage van het aantal broedende grutto-paren in het basisjaar. Als basisjaar is 1964 genomen.

In 1964 waren er ongeveer 126000 broedende grutto-paren in Nederland.
     

3p.

1.

Bereken met behulp van de grafiek het aantal broedende grutto-paren in 2005. Rond je antwoord af op duizendtallen.
       

Als de populatie van een bepaald soort vogels elk jaar afneemt, is de jaarlijkse groeifactor kleiner dan 1, waardoor deze soort op den duur met uitsterven bedreigd wordt.

Volgens Nederlandse onderzoekers hangt de groeifactor g voor veel vogelsoorten af van de volgende gegevens:
-

a,  de overlevingskans per jaar van nog niet broedrijpe vogels  (0 < a ≤ 1)
- s, de overlevingskans per jaar van broedvogels ( 0 < s ≤ 1)
- m, het gemiddeld aantal jongen per broedpaar per jaar.
De onderzoekers werken met het model:

       
Voor een vogelsoort in een bepaald gebied geldt: a = 0,81 en s = 0,81.
       

4p.

2.

Bereken vanaf welke waarde van m de populatie niet met uitsterven bedreigd wordt. Rond je antwoord af op 2 decimalen.
       

Volgens sommige onderzoekers is het voor het voortbestaan van een soort voldoende als broedparen gemiddeld per jaar 2 jongen hebben, dus als m = 2 .
We vragen ons af of er waarden van a en s zijn waarbij m = 2 niet voldoende is om er voor te zorgen dat g ≥ 1.
       

3p.

3.

 Onderzoek of er zulke waarden voor a en s zijn.
       

Zolang g = 1 geldt, wordt een vogelsoort nog net niet met uitsterven bedreigd. Als dan ook m = 1 geldt, kan het model herschreven worden tot:   s = √(2 - 2a)

Een bioloog beweert dat dit betekent dat bij g = 1 en m = 1 een toename van a een afname van s tot gevolg heeft.
       

4p.

4.

 Onderzoek of dit juist is met behulp van de afgeleide functie van s.
       
Bridgedrive.
       

Bridge is een kaartspel waarbij een team van twee spelers tegen een ander team van twee spelers speelt. Zo’n team van twee spelers heet een paar. De Oldenzaalse Bridge Club organiseert ieder jaar een bridgedrive (een toernooi) waar een groot aantal paren aan deelneemt.
Aan de bridgedrive van 2008 namen 192 paren deel. Elk paar speelde acht rondes waarin ze in elke ronde vier spellen speelden. Nadat elk paar deze 32 spellen had gespeeld werden de eindscores bepaald. Het paar met de hoogste eindscore werd de winnaar.
       

3p.

5.

Bereken hoeveel keer er tijdens deze bridgedrive een spelletje bridge werd gespeeld.
       

De bridgedrive wordt gespeeld op 16 verschillende horecalocaties in Oldenzaal. Op elke locatie spelen evenveel paren. Na vier spellen wisselen de paren van locatie volgens een schema dat de spelers van tevoren niet bekend is.

Het paar Hendriks-Hendriks zit klaar voor de eerste ronde. Zij vragen zich af of het paar Van Zomeren-Zenderink tijdens de eerste ronde op dezelfde locatie speelt.
       

3p.

6.

Bereken de kans dat het paar Van Zomeren-Zenderink de eerste ronde op dezelfde locatie speelt als het paar Hendriks-Hendriks.
       

Per spel krijgt elk paar een score op een schaal van 0 tot en met 100. Na afloop van de drive wordt voor elk paar de totale score gedeeld door het aantal gespeelde spellen. Dit geeft een eindscore die wordt afgerond op twee decimalen. Het paar met de hoogste eindscore krijgt positie 1 en wint de hoofdprijs.

We nemen aan dat in 2008 de eindscores normaal verdeeld waren met gemiddelde 50,00 en standaardafwijking 7,12. Het paar Hendriks- Hendriks had een eindscore van 54,66.
       

4p.

7.

 Bereken op grond hiervan de positie van dit paar in de eindklassering.
       

In 2007 namen 190 paren deel aan de drive. Hun eindscores staan in deze tabel. Het gemiddelde van deze eindscores is 49,93 en de standaardafwijking is 7,07.

Men vraagt zich af of deze scores ook bij benadering normaal verdeeld zijn. Dit is te onderzoeken door te controleren of deze gegevens in overeenstemming zijn met onder andere de volgende drie regels voor de normale verdeling:
1.  de 68%-vuistregel;
2.  de 95%-vuistregel;
3.  de mediaan is gelijk aan het gemiddelde.

Aan de eerste regel (de 68%-vuistregel) is voldaan.
       

5p.

8.

Onderzoek of de scores in deze tabel ook aan elk van de andere twee regels voldoen.
       

Het paar Fussel-Stoffer neemt voor het eerst deel. Gezien hun grote ervaring bij andere bridgetoernooien verwachten zij zelf een hoge klassering. “Tegen zulke tegenstanders hebben wij in ieder spel 80% kans op een score van 60 punten of meer”, zo menen zij.  Een toeschouwer vindt dit paar niet zo sterk en twijfelt aan deze uitspraak. Zij volgt de eerste 16 spellen. Op die spellen blijkt het paar 10 keer een score van 60 punten of meer gehaald te hebben.
       

6p.

9.

Formuleer een hypothesetoets en onderzoek of dit resultaat voldoende reden geeft om de toeschouwer gelijk te geven. Neem een significantieniveau van 5%.
       
Talen.
       

De wereldbevolking bedroeg in 2010 ongeveer 6800 miljoen (6,8 miljard) mensen. Volgens schattingen uit dat jaar werden er toen op de wereld ruim 500 talen gesproken.
In deze opgave verstaan we onder sprekers van een taal alleen de mensen voor wie deze taal hun moedertaal is.
Sommige talen worden door meer dan 100 miljoen mensen gesproken, maar er zijn ook talen die nog slechts door enkele tientallen mensen gesproken worden.

Hoe meer mensen een taal spreken, hoe groter we die taal noemen.
Alle aantallen in deze opgave hebben betrekking op het jaar 2010 en zijn benaderingen op grond van schattingen.
De grootste taal is het Mandarijn met 800 miljoen sprekers. De kans dat van 6 willekeurig gekozen mensen uit de totale
wereldbevolking er minstens één Mandarijn spreekt, is groter dan 0,5.
       

4p.

10.

 Bereken deze kans in drie decimalen nauwkeurig.
       

Van alle gesproken talen is er een ranglijst waar de talen op volgorde van veel naar weinig sprekers staan. De top-15 van de meest gesproken talen in 2010 staat in onderstaande tabel.
       
Mandarijn 800000000
Spaans 358000000
Engels 350000000
Hindi/Urdu 240000000
Bengaals 170000000
Russisch 160000000
Portugees 150000000
Arabisch 150000000
Japans 126000000
Duits 100000000
Wu 90000000
Javaans 70000000
Punjab 70000000
Frans 70000000
Telugu 70000000
       

Deze 15 talen hebben samen 2974 miljoen sprekers. Van de ruim 500 talen zijn er 86 talen met 10 miljoen of meer sprekers. Op de 44e plaats staat het Nederlands met 20 miljoen sprekers. Hieruit kun je concluderen dat de talen op de plaatsen 45 tot en met 86 elk minstens 10 miljoen en hoogstens 20 miljoen sprekers hebben.

Met deze gegevens kun je niet het exacte totaal aantal sprekers van de 86 talen met meer dan 10 miljoen sprekers berekenen. Wel is het mogelijk om een onder- en een bovengrens van dit aantal te berekenen.
       

4p.

11.

Laat zien dat het mogelijk is dat het totaal aantal sprekers van de eerste 86 talen groter is dan 5,7 miljard.
       

Onderzoekers willen een formule opstellen waarmee het totaal aantal sprekers van de n grootste talen berekend kan worden als n gegeven is.
Neem aan dat geen enkel tweetal talen precies hetzelfde aantal sprekers heeft.
       

3p.

12.

Beredeneer dat de grafiek van het totaal aantal sprekers afnemend stijgend is.
       

We ordenen de talen van groot naar klein en maken een staafdiagram met cumulatieve totalen. In onderstaande figuur is het staafdiagram weergegeven met op de horizontale as het plaatsnummer n van de 30 meest gesproken talen en op de verticale as het totaal aantal sprekers A in miljarden van de n grootste talen.
       
       

De 15e staaf in deze figuur geeft aan dat het totaal aantal sprekers van de 15 grootste talen 2974 miljoen (2,974 miljard) is.

De bovenkanten van de staven kunnen worden benaderd met een kromme die het verband tussen het totaal aantal sprekers A van de n grootste talen en n weergeeft. Een benadering van de kromme door de bovenkanten van de staven wordt gegeven door de formule:

A = 0,92 • n0,43

Hierbij is n het plaatsnummer van een taal en A het totaal aantal sprekers in miljarden van de n grootste talen.
       

4p.

13.

Toon met behulp van de afgeleide functie aan dat de grafiek van A inderdaad afnemend stijgend is.
       

De formule A = 0,92 • n0,43 kan ook gebruikt worden om te berekenen hoeveel talen er ten minste nodig zijn om een bepaald aantal mensen in hun eigen taal te kunnen bereiken. De formule kan hiervoor herleid worden tot de vorm:

n = b • Ac
       

4p.

14.

 Bereken b en c. Rond je antwoorden af op twee decimalen.
     

De formule A = 0,92 • n0,43 geeft voor kleine waarden van n een redelijke benadering van A. Een nadeel van deze formule is dat voor grote waarden van n het totaal aantal sprekers A groter wordt dan de totale wereldbevolking. Onderzoekers willen daarom een formule gebruiken waarin de waarde van A niet groter wordt dan 6,8. Daarom stelden zij voor een formule te gebruiken van de vorm:

A = 6,8(1 - gn)

Ook in deze formule is n het plaatsnummer van een taal en A het totaal aantal sprekers in miljarden van de n grootste talen.

Er is een waarde van g, waarbij deze nieuwe formule voor de 15 grootste talen het aantal van 2,974 miljard sprekers oplevert.
     

4p.

15.

 Bereken deze waarde van g in twee decimalen nauwkeurig.
       
Benzineverbruik.
       

Op sommige stukken snelweg staat een bord met de aansporing ‘Rij schoner, rij 80 in z’n 5.’
Naar aanleiding hiervan onderzocht een journalist hoe het benzineverbruik van een auto afhangt van de snelheid en de versnelling waarin de auto rijdt.

De journalist reed ’s nachts 6 keer een afstand van 10 km op een recht stuk snelweg. Met behulp van cruise control reed hij eerst met 80 km per uur in de derde, vierde en vijfde versnelling en vervolgens met 90 km per uur in de derde, vierde en vijfde versnelling.

De gemiddelde snelheid van de journalist over de 60 km was niet 85 km per uur.
       

4p.

16.

Toon aan dat de gemiddelde snelheid afgerond op één decimaal 84,7 km per uur is.
       

In de vijfde versnelling is de auto steeds het zuinigst. In de tabel staat de literafstand L (het aantal kilometer dat je per liter benzine kunt rijden) van de auto in de vijfde versnelling bij verschillende snelheden. In de tabel kun je bijvoorbeeld zien dat de literafstand van de auto bij een snelheid van 80 km per uur 21,62 km is. Dat betekent dat je bij deze snelheid 21,62 km kunt rijden met 1 liter benzine.
       
literafstand en de bijbehorende snelheid in de vijfde versnelling
snelheid v  (km/uur) 80 90 100 110
literafstand L (km) 21,62 19,88 17,82 15,95
       

De journalist stelde dat er tot een snelheid van 110 km per uur bij benadering sprake was van een lineair verband tussen de literafstand L en de snelheid v.
       

4p.

17.

Bereken met behulp van dit lineaire verband de literafstand bij een snelheid van 127 km per uur. Rond je antwoord af op één decimaal.
       

Het verband tussen de literafstand L en de snelheid v blijkt bij een snelheid boven 110 km per uur niet lineair te zijn.
In een voorlichtingsfolder over zuinig rijden lezen we: ‘Een zuinige snelheid is 90 km per uur. Als je 120 km per uur rijdt, dan neemt de literafstand met 30% af. Rijd je 140 km per uur, dan is de literafstand al met 48% afgenomen.’

Je kunt met bovenstaande gegevens berekenen met hoeveel procent de literafstand afneemt als de snelheid toeneemt van 120 km per uur naar 140 km per uur.
       

4p.

18.

 Bereken dit percentage.
       

 

Compressie.
       

Zonder dat je het merkt, heb je regelmatig te maken met gecomprimeerde computerbestanden. Daardoor passen er heel veel nummers op een iPod en past een hele film op een dvd. We bekijken in deze opgave een vereenvoudigde compressiemethode.

De rij 000000001111110000001 kan met deze methode gecomprimeerd worden tot 80616011. In de nieuwe rij wordt elk teken voorafgegaan door het aantal keren dat het voorkomt: 8 keer een 0, 6 keer een 1, 6 keer een 0 en nog één 1.
De oorspronkelijke rij van 21 tekens is zo teruggebracht tot 8 tekens. Als het aantal tekens na compressie kleiner is geworden, noemen we de compressie voordelig.
Voor deze rij is de compressieratio 0,62. De compressieratio kunnen we als volgt berekenen:
       

       

Bekijk de rij 001100110011000111000. Op deze rij wordt bovenstaande compressiemethode toegepast.
       

3p.

19.

Bereken de compressieratio van deze rij en geef aan of de compressie voordelig is.
       

Een rij met veel dezelfde tekens achter elkaar is natuurlijk beter te comprimeren dan een rij waarin de tekens vaak wisselen.
Bij een rij waarin de tekens vaak wisselen kan de compressieratio zelfs negatief worden. Het aantal tekens is dan na compressie groter dan ervoor.
       

3p.

20.

Onderzoek wat de kleinste waarde is die de compressieratio volgens de formule kan aannemen.
       

Omdat computerbestanden bestaan uit rijen tekens kunnen we hiervan ook de compressieratio berekenen.
Voor grote bestanden is er een verband tussen de compressieratio en het gemiddelde aantal gelijke tekens achter elkaar (de gemiddelde serielengte). Het verband hiertussen is in de figuur weergegeven.
       

       
Bij deze grafiek past de volgende formule:

       

Hierin is L de gemiddelde serielengte.

De compressieratio van een bestand is 0,40.
       

3p.

21.

Bereken met de formule de gemiddelde serielengte van dit bestand. Geef je antwoord in twee decimalen nauwkeurig.
       

Informatici doen veel onderzoek naar de compressie van grote bestanden. Zij genereren met behulp van een toevalsgenerator rijen enen en nullen om te onderzoeken onder welke omstandigheden compressie voordelig is.
Als de toevalsgenerator zo wordt ingesteld dat de kans op een 0 gelijk is aan 0,8 en de kans op een 1 gelijk is aan 0,2, dan zal er een behoorlijke kans zijn dat het begin van een rij uit 3 of meer dezelfde tekens bestaat.
       

4p.

22.

 Bereken deze kans.
       

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
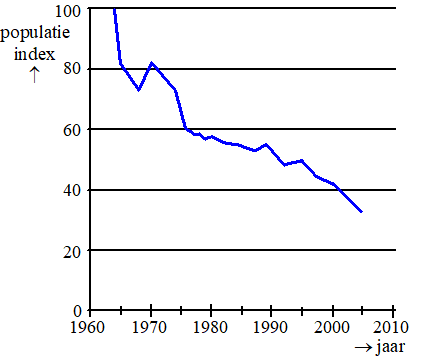
1. aflezen uit de grafiek:  in 2005 was het indexcijfer ongeveer 33.
indexcijfer 100 hoort bij 126000 grutto's
verhoudingstabel:
 
100 33
126000 ??
  ?? = 33 • 126000/100 = 41580
afgerond op duizendtallen is dat 42000.
   
2. de grenswaarde voor uitsterven is g = 1.
1 = (0,81 + √(0,6561 + 1,3122m)/2
2 = 0,81 + √(0,6561 + 1,3122m
1,19 = √(0,6561 + 1,3122m)
1,4161 = 0,6561 + 1,3122m
0,76 = 1,3122m
m = 0,5791...
afgerond  m = 0,58 
   
3. m = 2 en g = 1  geeft 1 = (a + √(a² + 4s²))/2 

Door a en s klein genoeg te nemen moet je onder de 1 kunnen komen.
bijv.  a = 0,01 en s = 0,01  geeft  g = 0,016
zulke waarden van a en s bestaan dus WEL.
   
4. s = √(2 - 2a) = (2 - 2a)0,5
s ' =  0,5(2 - 2a)-0,5 • -2
s ' =  -1/√(2 - 2a) 
omdat die wortel altijd een positief getal is, is s' altijd negatief.
dus de grafiek daalt, dus een toename van a geeft een afname van s
de bewering is juist.
   
5. bij 8 rondes van 4 spellen speelt elk paar 32 spellen
bij 192 paren zijn dat 32 • 192 = 6144 spellen
maar nu is elk spel dubbel geteld (want aan een spel doen 2 paren mee)
dus er zijn 6144/2 = 3072 spellen gespeeld.
   
6. op elke locatie spelen 192/16 = 12 paren.
behalve het paar Hendriks-Hendriks spelen er dus nog 11 andere paren op deze locatie.
In totaal zijn er 191 andere paren.
De kans dat Van Zomeren-Zenderink ook op deze locatie speelt is dus  11/191
   
7. De kans dat een willekeurig paar een hogere score haalt is   P( X > 54,66 met μ = 50,00 en σ = 7,12)
P(X > 54,66) = 1 - P(X < 54,66) = 1 - normalcdf(0, 54.66, 50.00, 7.12) = 0,2564
Dus naar verwachting zullen er 0,2564 • 192 = 49,2... paren hoger eindigen
De verwachte positie is dus plaats 50.
   
8. μ + 2σ = 49,93 + 2 • 7,07 = 64,07
μ - 2σ = 49,93 - 2 • 7,07 = 35,79
en de tabel vallen de nummers  1 tm 4 en 186 tm 190 daarbuiten
Dat zijn er 4 + 5 = 9  en dat is  9/190 • 100% = 4,7%
Dus ertussen valt 95,3% en dat klopt aardig met regel 2.

de mediaan is nummer  (190 + 1)/2 = 95,5  dus tussen de nummers 95 en 96
Dat is (50,35 + 50,34)/2 = 50,345
dat is niet gelijk aan het gemiddelde (49,93) dus aan de derde regel is niet voldaan.
   
9. H0:  p(60 punten of meer) = 0,80
H1:  p < 0,80
meting is 10 van de 16
overschrijdingskans = P(X ≤ 10) = binomcdf(16, 0.80, 10) = 0,082
dat is groter dan 0,05 dus er is NIET voldoende reden om de toeschouwer gelijk te geven (H0 aannemen).
   
10. de kans dat een willekeurig persoon Mandarijn spreekt is 800/6800 = 0,1176
omdat de wereldbevolking nogal groot is mag je dit beschouwen als een experiment met terugleggen, dus binomiaal.
n =  6,  p = 0,1176
P(minstens één) = 1 - P(geen) = 1 - binomcdf(6, 0.1176, 0) = 0,528
dat is inderdaad meer dan 50%

OF
P(mandarijn) = 0,1176 dus P(geen mandarijn) = 0,8824
P(6 keer niet) = 0,88246 = 0,4720
P(minstens één wel) = 1 - 0,4720 = 0,528
   
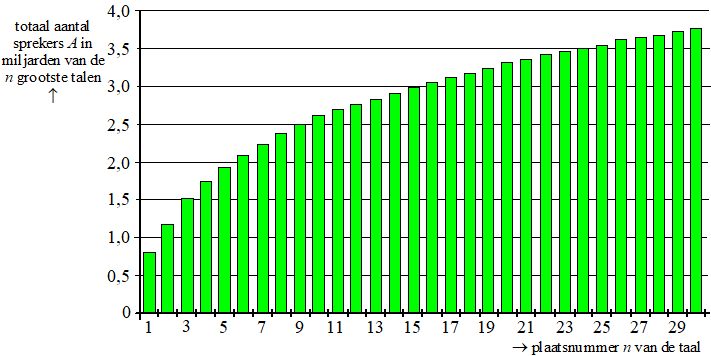
11. de eerste 15 talen hebben samen 2974 miljoen sprekers.

nrs.  16 tm 44 hebben tussen de  70 miljoen en 20 miljoen sprekers
dat zijn 29 talen, met in totaal tussen de 29 • 70 = 2030 miljoen en 29 • 20 = 580 miljoen sprekers.

nrs. 45 tot en met 86 hebben elk minstens 10 miljoen en hoogstens 20 miljoen sprekers.
Dat zijn 42 talen met in totaal tussen de 42 • 10 = 420 miljoen en 42 • 20 = 840 miljoen sprekers.

meer dan 10 miljoen ligt tussen de 2974 + 580 + 420 = 3974 miljoen sprekers en  2974 + 2030 + 840 = 5844 miljoen sprekers.

5,7 miljard is  5700 miljoen, dus dat is inderdaad mogelijk.
   
12. er komt van een nummer naar het volgende steeds iets bij dus de grafiek stijgt.

omdat de talen op volorde van klein naar groot staan wordt  de hoeveelheid die erbij komt steeds kleiner, dus de grafiek is afnemend stijgend.
   
13. A = 0,92 • n0,43 
A' = 0,43 • 0,92 • n-0,57  = 0,3956/n0,57 

de afgeleide is altijd positief, dus de grafiek van A is stijgend.

als n groter wordt, dan wordt n0,57 ook groter dus dan wordt van de afgeleide de noemer groter.
dan wordt de afgeleide zelf kleiner
dus wordt de stijging van A kleiner als n groter wordt.
   
14. A = 0,92 • n0,43
  1/0,92  A = n0,43
1,08...•A = n0,43
n = (1,08... • A)1/0,43
n = 1,08...1/0,43 • A1/0,43
n = 1,08...2,32... • A2,33
n = 1,21 • A2,33
dus b = 1,21 en c = 2,33
   
15. A = 6,8(1 - gn)
n = 15 geeft A = 2974
2,974 = 6,8(1 - g15)
0,437... = 1 - g15
g15 = 0,562...
g = 0,562...1/15 = 0,96
   
16. Hij reed 30 km met 80 km/uur en 30 km met 90 km/uur
30 km met 80 km/uur kost  30/80 uur
30 km met 90 km/uur kost  30/90 uur
In totaal kostte het rijden dus  30/80 + 30/90 = 0,7083... uur
De afstand was 60 km, dus de snelheid gemiddeld  60/0,7083... = 84,7 km/uur.
   
17. lijn door (80, 21.62) en  (110, 15.95)
a = (15.95 - 21.62)/(110 - 80) = -0,189
L = -0,189v + b
21.62 = -0,189 • 80 + b  geeft  b = 36,74 
dus L = -0,189v + 36,74
v = 127 geeft dan  L = 12,7 km
   
18. v = 90  geeft  L = 19,88
v = 120 geeft 30% afname dus L = 0,7 • 19,88 = 13,916 km
v = 140 geeft 48% afname, dus L = 0,52 • 19,88 = 10,3376
De afname tussen 120 en 140 is van  13,916 naar  10,3376
Dat is een verschil van 3,5784 en dat is  3,5784/13,916 • 100% = 25,7%
   
19. 001100110011000111000 dus voor compressie zijn er 21 tekens
compressie geeft de rij 202120212021303130  en dat zijn 18 tekens
compressieratio = (21 - 18)/21 = 0,1428...
de compressie is voordelig want het aantal tekens na compressie is kleiner dan het aantal voor compressie.
   
20. de compressie is het kleinst als er na iedere teken wisseling is.
bijv. de rij 1010101010101...  wordt  1110111011101110.... en dat is dubbel zoveel tekens.
dus aantal na compressie  = 2 • aantal voor compressie.
Stel dat er X tekens voor compressie zijn.
compressieratio = (X - 2X)/X = -1
   
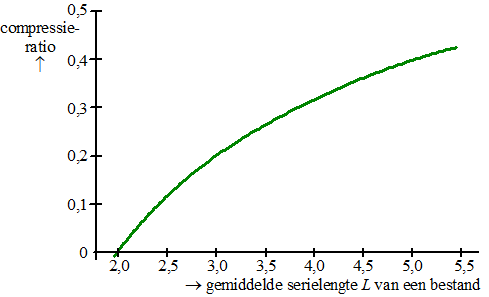
21. 0,4 = 1 - 1,4709/L0,561 
1,4709/L0,561 = 0,6
L0,561 = 1,4709/0,6 = 2,4515
L = 2,45151/0,561  = 4,95
   
22. P(3 of meer dezelfde tekens) = P(000... of 111....) =  P(000....) + P(111....)
= 0,83 + 0,23
= 0,52