VWO WA, 2018 - I

 

Windenergie.
       

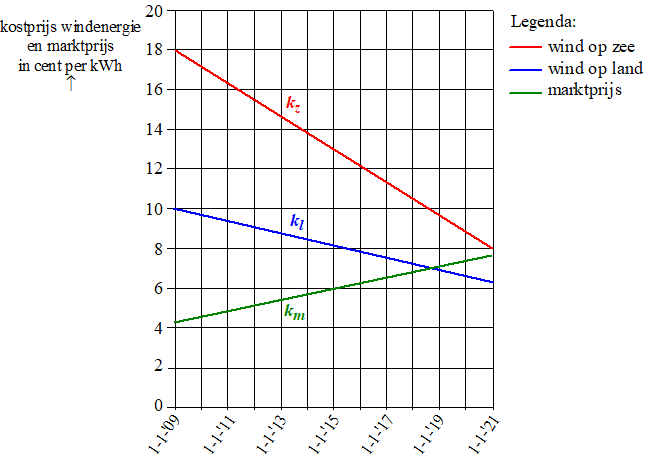
In een krant stond eind 2013 bij een artikel over de toekomst van windenergie de onderstaande figuur. In de figuur wordt de kostprijs voor het produceren van windenergie vergeleken met de kosten voor het produceren van energie in een traditionele kolencentrale (de marktprijs).
       

       

De grafieken zijn gebaseerd op een model van de werkelijkheid. Met behulp van dit model is het mogelijk om op ieder willekeurig tijdstip de kostprijs van energie uit te rekenen.

De formule voor de marktprijs km luidt:

km = 0,28 • t + 4,3

De formule voor de kostprijs van windenergie kl  van windmolens op land luidt:

kl = -0,31 • t + 10,0

Voor beide formules geldt: k is de prijs in cent per kWh (kilowattuur) en t is de tijd in jaren met t = 0 op 1 januari 2009.

We nemen in deze opgave aan dat de prijzen zich ook na 2020 volgens deze lineaire verbanden blijven ontwikkelen.
Door de duurdere windmolens op zee is de kostprijs van windenergie van die windmolens op dit moment nog steeds hoger dan die van windmolens op land. Maar door de voortdurende innovaties gaat dat veranderen.
       

5p.

1.

Stel met behulp van de figuur een formule op voor de kostprijs kz  van windenergie van windmolens op zee en bereken daarmee in welk jaar de windenergie van land en die van zee evenveel kosten.
       

Rond 2011 was de kostprijs van windenergie van windmolens op land nog tweemaal zo hoog als de marktprijs.
       

4p.

2.

Bereken in welk jaar de marktprijs tweemaal zo hoog zal zijn als de kostprijs van windenergie van windmolens op land.
       

In 2009 werd er in totaal 23,4 miljoen MWh energie door kolencentrales geproduceerd (1 MWh is 1 megawattuur, dat is 1000 kWh). De overheid heeft als doelstelling dat op den duur alle energie duurzaam moet worden geproduceerd. Energie die in kolencentrales wordt geproduceerd valt niet onder duurzaam geproduceerde energie.

We willen nu een model maken voor de totale kosten TK van de door kolencentrales geproduceerde energie in de jaren 2009-2050. Daarvoor doen we twee aannames:
1.

De totale hoeveelheid energie TE die per jaar door kolencentrales geproduceerd wordt, neemt lineair af van 23,4 miljoen MWh in 2009 tot 0 MWh in 2050. Er geldt dan:
 

 

In deze formule is TE in miljoenen MWh en j in jaren met j = 0 het jaar 2009. Bovendien is j een geheel getal.
2.

Om de totale kosten TK van energie te berekenen in een bepaald jaar, gebruiken we de gemiddelde marktprijs gm in euro per MWh in dat jaar. Er geldt:

gm = 2,8 •  j + 44,4

In deze formule is gm in euro per MWh en j in jaren met j = 0 het jaar 2009. Ook nu is j een geheel getal.
       

De totale kosten TK in een bepaald jaar zijn te berekenen door de door kolencentrales geproduceerde energie te vermenigvuldigen met de gemiddelde marktprijs in dat jaar. De formule voor TK is te schrijven als

TK = a • j2  + b • j + c .

In deze formule is TK in miljoenen euro’s en j in jaren met j = 0 het jaar 2009 en is j een geheel getal.
       

4p.

3.

Bereken de waarden van a, b en c in deze formule. Rond je antwoorden af op één decimaal.
       
Shannon-index.
       

De Shannon-index H is een maat voor de diversiteit (verscheidenheid) van een dieren- of plantenpopulatie in een gebied. Hoe hoger de Shannon-index, hoe groter de diversiteit.
We kijken naar een gebied met twee soorten bomen. De formule voor de Shannon-index is dan:

H = - ( p1 ln( p1) + p2 ln( p2 ))

waarin p1 en p2 de aandelen van elke soort binnen het gebied zijn. Er geldt bijvoorbeeld dat p1 = 0,37 als 37% van de bomen uit soort 1 bestaat.

Bos A bestaat voor 70% uit eiken en voor 30% uit beuken en bos B bestaat voor 90% uit eiken en voor 10% uit beuken.
       

3p.

4.

Onderzoek met de formule voor H van welk van beide bossen de Shannon-index het grootst is.
       

In een bos met twee soorten bomen, eiken en beuken, geldt: als p het aandeel eiken is, is het aandeel beuken gelijk
aan 1 – p. De formule voor de Shannon-index kan dan geschreven worden als:

H = - (pln( p) + (1 - p)ln(1 - p))
       

3p.

5.

Onderzoek met de grafische rekenmachine tot welke waarde de Shannonindex nadert als het aandeel eiken in het bos steeds kleiner wordt.
       

Met behulp van de afgeleide van H kunnen we onderzoeken bij welke verhouding eiken en beuken de Shannon-index maximaal is. Er geldt:

       

4p.

6.

Bereken met behulp van  dH/dp voor welke percentages eiken en beuken de Shannon-index H van het bos maximaal is.
       
Bitcoins.
       

De bitcoin is een digitale munteenheid die alleen online bestaat. Hij bestaat sinds 1 januari 2009 en kan worden gebruikt om te betalen in webwinkels of voor andere online diensten.

Bitcoins worden niet, zoals normaal geld, door een centrale bank in omloop gebracht. In plaats daarvan zijn alle bitcoins die in omloop zijn, gecreëerd door computers mee te laten werken aan oplossingen van geselecteerde wiskundige problemen. Dat werkt als volgt:
Iedereen kan op zijn of haar computer speciale software laten draaien die meewerkt aan het oplossen van zo'n wiskundig probleem. De eigenaar van de computer die de oplossing voor een probleem vindt, krijgt daarvoor 25 (nieuw gecreëerde) bitcoins als beloning. Omdat er in 2014 iedere 10 minuten zo'n probleem werd opgelost, werden er op deze manier iedere 10 minuten 25 bitcoins in omloop gebracht.

Op 1 januari 2014 waren er (ongeveer) 12,2 miljoen bitcoins in omloop.
       

3p.

7.

Bereken uitgaande hiervan in welk jaar het aantal bitcoins in omloop boven de 18 miljoen uitstijgt als de snelheid waarmee bitcoins in omloop gebracht worden niet verandert.
       

In werkelijkheid blijft de snelheid waarmee bitcoins in omloop worden gebracht niet gelijk aan 25 bitcoins per 10 minuten. Deze snelheid neemt namelijk af. Gedurende de eerste vier jaar, van 1 januari 2009 tot 1 januari 2013, was de beloning per oplossing nog 50 bitcoins. De beloning voor het vinden van een oplossing wordt elke vier jaar gehalveerd: van 1 januari 2013 tot 1 januari 2017 is de beloning per oplossing 25 bitcoins, voor de vier jaar erna 12,5 bitcoins per oplossing enzovoorts.
       

4p.

8.

Bereken vanaf welk jaar de beloning per oplossing minder dan één bitcoin zal zijn.
       

Het totale aantal bitcoins dat in omloop gebracht kan worden, is begrensd.
Dat is een gevolg van (onder andere) het feit dat de beloning per oplossing steeds gehalveerd wordt. Het totale aantal bitcoins dat in omloop is, kan worden benaderd met de formule:

C = 21 -  21 • 0,50,25 • t

Hierin is C het totale aantal bitcoins in miljoenen en t de tijd in jaren met t = 0 op 1 januari 2009.
       

3p.

9.

Bepaal met behulp van een redenering aan de hand van de formule de grenswaarde van het totale aantal bitcoins dat in omloop is.
       

Om het totale aantal bitcoins dat in omloop is te reguleren, wordt niet alleen het aantal bitcoins per oplossing kleiner gemaakt, maar wordt ook de moeilijkheidsgraad van de wiskundige problemen steeds groter gemaakt. Er zijn namelijk steeds meer mensen die hun computers mee laten rekenen.

De moeilijkheidsgraad van de problemen stijgt exponentieel volgens de formule D = 3,65• e0,533•t .

Hierin is D een maat voor de moeilijkheidsgraad en t de tijd in maanden met t = 0 op 1 januari 2013. Hierbij geldt dat hoe groter D is, hoe moeilijker het op te lossen probleem is.
       

4p.

10.

Stel de formule van de afgeleide van D op en beredeneer hoe je aan deze formule kunt zien dat de grafiek van D toenemend stijgend is.
       

De formule kan zó worden herschreven dat je een moeilijkheidsgraad kunt invullen en zo de tijd in maanden kunt berekenen die nodig is om die moeilijkheidsgraad te bereiken.
       

4p.

11.

 Herschrijf de formule D = 3,65 • e0,533•t  zó dat t wordt uitgedrukt in D.
       
Jaarringen.
       

Op de foto zie je een doorgezaagde boomstam. Hierin zijn zogenaamde jaarringen te zien. Deze ontstaan doordat de boom in de zomer snel groeit: dan wordt er licht gekleurd hout gevormd.
In de winter groeit de boom langzaam en wordt er donker gekleurd hout gevormd. Zo komt er elk jaar een ring bij, die uit een licht en een donker gedeelte bestaat: een jaarring.

In deze opgave kijken we eerst naar de groeisnelheid van de diameter (G) van een grove den. Omdat een boom afwisselend snel en langzaam groeit, kun je deze groeisnelheid modelleren met behulp van sinusoïden.

       

Voor de groeisnelheid van de diameter van een grove den gelden de volgende eigenschappen:
-

de groeisnelheid is drie maanden na het ontkiemen van het zaadje maximaal;
-

de groeisnelheid is negen maanden na het ontkiemen minimaal;
-

dit patroon herhaalt zich elk jaar;
-

de maximale groeisnelheid is 2,1 cm per jaar;
-

de minimale groeisnelheid is 0,3 cm per jaar.
       

Voor de groeisnelheid van de grove den kun je op basis van deze eigenschappen een formule opstellen van de vorm
G = a + bsin(c(t - d)) .

Hierin is G de groeisnelheid in cm per jaar en t de tijd in jaren na het ontkiemen.
       

4p.

12.

Bereken de waarden van a, b, c en d in deze formule. Licht je antwoord toe.
       

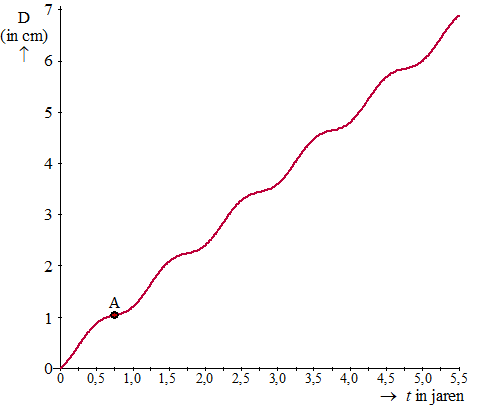
Nu bekijken we de diameter van de stam van deze grove den. Daarbij kan de volgende formule worden opgesteld:

D =1,2t + 0,14 + 0,14sin(2π(t - 0,25))

Hierin is D de diameter van de stam in cm en t de tijd in jaren na het ontkiemen met t = 0 op het moment van ontkiemen.
De grafiek van D is in de figuur getekend.
       

       

3p.

13.

Bereken met behulp van de formule op welk tijdstip de diameter een dikte van 5 cm bereikt. Rond je antwoord af op hele maanden.
       

In de grafiek is te zien dat de diameter schommelt rondom een lijn. De formule van deze lijn is T = 1,2t + 0,14.

In plaats van de diameter te berekenen met de formule voor D is deze ook te benaderen met behulp van de formule van de lijn. Deze benadering zal in de meeste gevallen iets afwijken van de diameter volgens de formule van D.
       

3p.

14.

 Onderzoek hoe groot deze afwijking maximaal kan zijn.
       

De diameter van de grove den groeit in de eerste zes maanden na het ontkiemen meer dan in de tweede zes maanden na het ontkiemen. Dat wisselen van groeisnelheid herhaalt zich zo in de jaren daarna.
       

3p.

15.

Bereken met behulp van de formule van D hoeveel procent van de jaarlijkse groei in de eerste helft van het jaar plaatsvindt. Rond je antwoord af op gehele procenten.
       

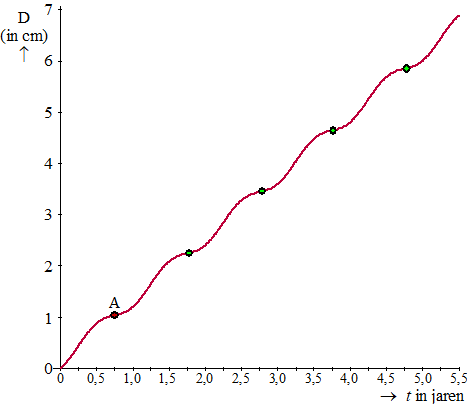
In het begin van deze opgave staat vermeld dat de groeisnelheid van de diameter G na negen maanden ( t = 0,75 ) minimaal is, namelijk 0,3 cm per jaar. De minimale groeisnelheid bij t = 0,75 die met de formule van D berekend wordt (zie punt A in de grafiek), is niet precies gelijk aan 0,3 cm per jaar.
       

3p.

16.

Geef in de grafiek van D nog een ander punt A aan waar de groeisnelheid volgens de formule van D minimaal is en bereken de minimale groeisnelheid in cm/jaar met de grafische rekenmachine. Rond je antwoord af op twee decimalen.
       
Toren van achtvlakken.
       

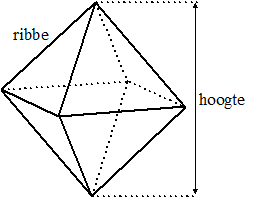
Op de afbeelding zie je een kunstwerk van Elt de Boer: een toren van regelmatige achtvlakken op een voet. Het bovenste deel van de voet is de helft van een regelmatig achtvlak met daaronder een kubus waarvan de ribbe dezelfde lengte heeft als die van het halve achtvlak. Daarboven zie je negen hele achtvlakken die naar boven toe steeds kleiner worden.

De kunstenaar maakt de voet zwart en van de 9 achtvlakken maakt hij 3 achtvlakken rood, 3 oranje en 3 geel.

 
     

4p.

17.

Bereken op hoeveel manieren de kunstenaar dit kan doen.

Een regelmatig achtvlak, zie de figuur, heeft 12 ribben die allemaal even lang zijn. De ribbe van de voet is 20 cm en die van het bovenste achtvlak is 4 cm.

De achtvlakken worden naar boven toe steeds kleiner. De kunstenaar kan ervoor kiezen de ribbe van de achtvlakken steeds met een vaste factor r te vermenigvuldigen. Afgerond op twee decimalen geldt dan:

r = 0,84

       

3p.

18.

 Bereken de waarde van r in drie decimalen nauwkeurig.
       

De kunstenaar had er ook voor kunnen kiezen om de ribbe met een vaste lengte te laten afnemen. De lengten van de ribben van de opeenvolgende achtvlakken vormen dan een rekenkundige rij. Deze rij kan benaderd worden met de directe formule in de vorm van een lineaire formule:   un = 20 -1,78n

Hierin is n het nummer van het achtvlak. In de formule is un de lengte in cm van de ribbe van het n-de achtvlak. Bij n = 0 hoort de lengte van de ribbe van de voet.
       

3p.

19.

Laat zien hoe de lineaire formule un = 20 - 1,78n afgeleid kan worden uit de gegevens.
       

De twee methoden zullen in het algemeen verschillende lengtes geven voor de ribben van de achtvlakken uit de serie.
       

4p.

20.

Onderzoek bij welk achtvlak uit de serie dit verschil maximaal is en geef ook aan hoe groot dat verschil is. Rond je antwoord af op gehele millimeters.
       
Sprinttrein.
       

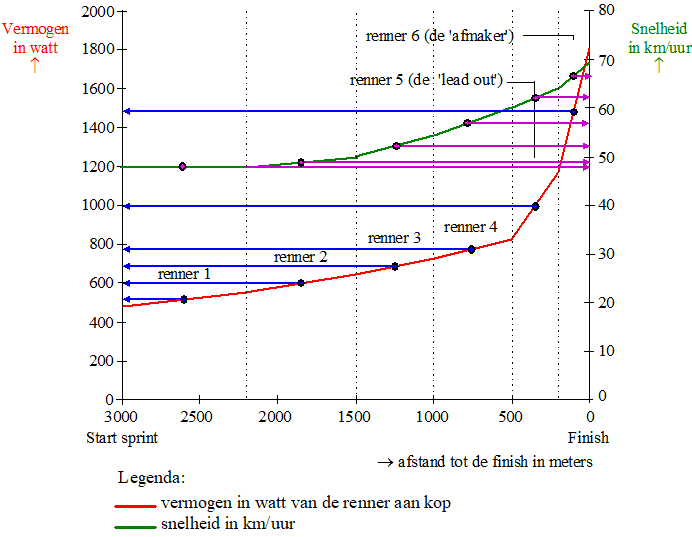
Veel wielerwedstrijden worden beslist in een massasprint. Er zijn ploegen die zich hierin hebben gespecialiseerd. Zij stellen een zogenaamde sprinttrein van zes wielrenners samen, die ervoor moet zorgen dat hun ploeg de wedstrijd wint.

De ploeg Giant-Shimano, met de Duitse sprinter Marcel Kittel, heeft op deze wijze een aantal etappes gewonnen in de Tour de France van 2014.

Een sprinttrein werkt als volgt: vanaf drie kilometer voor de finish gaan zes renners van de ploeg om beurten aan kop rijden. Daarbij voeren ze geleidelijk de snelheid op, waarna de zesde renner de taak heeft de massasprint te winnen.

In een krant stond de volgende figuur. Hierin is weergegeven welk vermogen en welke snelheid de renners bereiken wanneer zij aan kop rijden.
       

       

Met de gegevens uit de figuur is voor iedere renner de geleverde arbeid te berekenen. De arbeid van een renner is gelijk aan het vermogen vermenigvuldigd met de tijdsduur in seconden.
Een wielerliefhebber wil onderzoeken of een renner aan kop aan het eind van de sprint meer, dezelfde of minder arbeid levert dan een renner aan kop aan het begin van de sprint.
       

7p.

21.

Voer dit onderzoek uit door vermogens en snelheden te kiezen bij de door jou gekozen renners en maak daarbij gebruik van de figuur.
       

 

 

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. in 2009 is de prijs 18, en in 2021 is de prijs 8
Dat geeft de punten  (0, 18) en (12, 8)
a = (8 - 18)/(12 - 0) = -10/12 = -5/6
b = 18 want de lijn gaat door (0, 18)
De formule is  kz = -5/6 • t + 18
Als ze evenveel kosten moet gelden  -5/6t + 18 = -0,31t + 10,0
-0,5233...t = -8
t = 15,28....
Dat is in het jaar 2024.   
   
2. km = 2 • kl
0,28t + 4,3 = 2 • (-0,31t + 10,0)
0,28t + 4,3 = -0,62t + 20,0
0,90t = 15,7
t = 15,7/0,90 = 17,44....
Dat is dus in het jaar 2026.
   
3. TK = TE • gm
TK = (23,4 - 23,4/41 • j) • (2,8j + 44,4)
TK = (23,4 - 0,57.. • j) • (2,8j + 44,4)
TK = 23,4 • 2,8j + 23,4 • 44,4 - 0,57j • 2,8j - 0,57j• 44,4
TK = 65,52j + 1038,96 - 1,598..• j2 - 25,34...• j
TK = -1,6j2 + 40,2j + 1039,0

a = -1,6
b = 40,2
c = 1039,0 
   
4. HA = -(0,7ln(0,7) + 0,3ln(0,3)) = 0,61
HB = -(0,9ln(0,9) + 0,1ln(0,1)) = 0,33
Dus de Shannon-index van bos A is het grootst.
   
5. Als het aandeel eiken steeds kleiner wordt gaat p naar nul toe.
p = 0,1 geeft H = 0,33
p = 0,01 geeft  H = 0,056
p = 0,001  geeft  H = 0,0079
p = 0,0001 geeft  H = 0,0010
Dat nadert tot nul.
   
6. Voor het maximum moet gelden  H ' = 0
-lnp + ln(1 - p) = 0
lnp = ln(1 - p)
p = 1- p
2p = 1
p = 0,5
Dus 50% eiken en 50% beuken.
   
7. 25 bitcoins per 10 minuten is 150 bitcoins per uur
Dat is 150 • 24 = 3600 bitcoins per dag.
Er moeten nog 18 - 12,2 = 5,8 miljoen bitcoins komen.
Dat duurt dus  5800000/3600 = 1611,11... dagen
Dat is 1611,11/365 = 4,41 jaar
In 2018 zal het aantal boven de 18 miljoen uitkomen.
   
8. in 2009 was het 50, maar elke 4 jaar wordt het gehalveerd.
Hoe vaak moet je 50 halveren om 1 te krijgen?
50 - 25 - 12,5 - 6,25 - 3,125 - 1,5625 - 0,78125
50 moet zes keer gehalveerd worden.
Dat duurt dus 6 periodes van 4 jaar, en dat zal zijn in 2009 + 6 • 4 = 2033
   
9. C = 21 -  21 • 0,50,25 • t
als t steeds groter wordt, wordt 0,25t ook steeds groter
dan wordt  0,50,25t  steeds kleiner:  het gaat naar nul toe.
dan gaat 21 • 0,50,25t ook naar nul
dan gaat C naar 21 toe.
De grenswaarde is dus 21 miljoen.
   
10. D = 3,65• e0,533•t
D' = 3,65 • e0,533t • 0,533

t is positief, dus e0,533t is ook positief.
Dus de hele afgeleide is positief dus D stijgt.

als t groter wordt, dan wordt  0,533t ook groter
dan wordt  e0,533t ook groter, dus wordt de afgeleide ook groter.
Dus de stijging is toenemend.
   
11. D = 3,65• e0,533•t
e0,533t = D/3,65
e0,533t = D/3,65
ln(e0,533t) = ln( D/3,65)
0,533t = ln( D/3,65)
t = 1/0,533 • ln( D/3,65)
   
12. de snelheid varieert tussen 2,1 en 0,3 dus de evenwichtsstand is (2,1 + 0,3)/2 = 1,2 = a
de amplitude is de afstand van evenwichtslijn tot maximum dus 2,1 - 1,2 = 0,9 = b
de periode is 1 jaar, dus  c = 2π/1 = 2π
het maximum zit bij 3 maanden en dat is 0,25 jaar, de grafiek gaat een kwart periode daarvóór door de evenwichtsstand omhoog, dus dat is bij  t = 0,  dus  d = 0.
   
13. Y1 = 5
Y2 = 1,2X + 0,14 + 0,14*sin(2π * (X - 0,25))
(denk erom dat de GR op radialen staat!)
intersect geeft dan  t= 4,12....
4,12... • 12  is na 50 maanden.
   
14. De afwijking is het verschil tussen T en D dus dat is T - D
Y2 als in vraag 13.
Y1 = Y2 - (1,2X + 0,14)    (Y2 vind je bij VARS - YVARS - Function)
calc - maximum geeft dan  0,14.

OF
Het verschil tussen beide formules is alleen dat sinusdeel, en dat is maximaal 0,14 (want dat is de amplitude ervan)
   
15. Y1 =1,2X + 0,14 + 0,14sin(2π(X - 0,25))
TABLE  (TBLSET  met TBLStart = 0 en ΔTbl = 0,5)
D(0) = 0
D(0,5) = 0,88
D(1) = 1,2
dat is  0,88/1,2 • 100% = 73%
   
16.
  Zie de groene punten in bovenstaande figuur
Y1 = 1,2X + 0,14 + 0,14sin(2π(X - 0,25))
calc - 6:dy/dx  en dan  X =  0,75  geeft helling  ongeveer 0,32 cm/jaar
   
17. Het is een rijtje letters RRROOOGGG
Voor de drie RRR zijn er  9 nCr 3 = 84 mogelijkheden
Voor de drie OOO daarna nog  6 nCr 3 = 20 mogelijkheden
(de drie GGG liggen daarna vast)
In totaal zijn dat 20 • 84 = 1680 mogelijkheden.
   
18. In negen stapjes wordt het verkleind van 20 naar 4
Dat is een factor  4/20 = 0,2
Per stapje is dat 0,21/9 = 0,836 
   
19. De lengte van de ribbe neemt regelmatig af van 20 tot 4
Dat is afname 16 in 9 stappen
Per stap is dat 16/9 = -1,78
De beginwaarde is u0 = 20
Dat verklaart de formule.
   
20. exponentieel:  u = 20 • 0,84n
lineair  u = 20 - 1,78n

Y1 = 20 * 0,84^X
Y2 = 20 - 1,78X
Y3 = Y1 - Y2   (Y1 en Y2 vind je bij VARS - YVARS - Function)
Kijk in de TABLE waar Y3 maximaal is  (positief of negatief)
Dat is bij n = 4 en daar is het verschil 29 mm
   
21.
   
 
renner gem. snelheid
(zie figuur)		 gem. vermogen
(zie figuur)		 afstand tijd
=afst./snelh.		 arbeid
= tijd • gem. vermogen
1 48 km/u = 13,33 m/s 510 3000-2200 = 800 60,0 60,0 • 510 = 30600
2 49 km/u = 13,61 m/s 600 2200-1500 = 700 51,4 51,4 • 600 = 30840
3 52 km/u = 14,44 m/s 690 1500-1000 = 500 34,6 34,6 • 690 = 23874
4 57 km/u = 15,83 m/s 780 1000-500 = 500 31,6 31,6 • 780 = 24648
5 62 km/u = 17,22 m/s 1000 500 - 200 = 300 17,4 17,4 • 1000 = 17400
6 66 km/u = 18,33 m/s 1490 200 - 0 = 200 10,9 10,9 • 1490 = 16241
   
  (de m/s zijn gevonden door de km/uur te delen door 3,6)
conclusie: renners aan het eind aan kop  leveren minder arbeid dan renners aan het begin aan kop