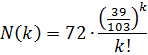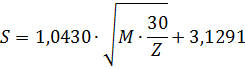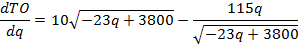VWO WA, 2016 - II

 

Hittegolven in Nederland
       

In Nederland is er sprake van een hittegolf als de maximumtemperatuur in De Bilt gedurende minstens 5 opeenvolgende dagen 25 °C of hoger is en bovendien op minstens 3 van deze dagen de maximumtemperatuur 30 °C of hoger is.

In deze tabel staat een overzicht van alle 39 hittegolven in Nederland in de periode 1911-2013.

Van elke hittegolf is het aantal dagen aangegeven in de tabel.
Volgens Joost heeft een willekeurig gekozen dag uit de periode 1911-2013 (dus inclusief de wintermaanden) een kans van ongeveer 1% om in een hittegolf voor te komen.
       

3p.

1.

Onderzoek of dit juist is. Hierbij hoef je geen rekening te houden met schrikkeljaren.
     

 

Er zijn jaren waarin er geen of precies één hittegolf voorkomt. Er zijn ook jaren waarin er twee of nog meer hittegolven voorkomen, bijvoorbeeld 1911.
Een wiskundige heeft op basis van deze periode van 103 jaar een model opgesteld voor het aantal jaren waarin k hittegolven in één jaar voorkomen (met k = 0,1, 2, 3, 4 ).

Bij dit model hoort de volgende formule:

       

De afgeronde waarde van N is het aantal jaren dat er naar verwachting k hittegolven in één jaar voorkomen.
       

5p.

2.

Onderzoek of er waarden van k zijn waarbij dit model meer dan 1 afwijkt van het werkelijke aantal jaren in de periode 1911-2013 dat er k hittegolven in één jaar voorkomen. Licht je antwoord toe.
     

 

In deze tabel zijn de maximumtemperaturen van elk van deze 39 hittegolven vermeld. Joost vermoedt dat de maximumtemperaturen van hittegolven normaal verdeeld zijn.
       

6p.

3.

Onderzoek met behulp van normaal-waarschijnlijkheidspapier of de maximumtemperaturen van de 39 hittegolven in deze tabel aanleiding zijn om Joost gelijk te geven. Neem de eerste klasse van 30 tot en met 31, dus de klasse 〈30,31] .
     

 
SMOG - index
       

Er is veel onderzoek gedaan naar de moeilijkheidsgraad van teksten. Er zijn dan ook verschillende manieren om die in een getal uit te drukken. Deze opgave gaat over één van die manieren.

Begin 2014 publiceerde NRC Handelsblad het volgende fragment uit een artikel over de gebruiksvoorwaarden van Googlesoftware.
       
Fragment.

Google’s gebruiksvoorwaarden worden met argusogen gevolgd door privacywaakhonden als Bits of Freedom en het College Bescherming Persoonsgegevens. Ze hebben het vaak over de inhoud van zulke teksten, maar hoe zit het met de moeilijkheidsgraad van de teksten? Die is hoog bij Google’s privacyvoorwaarden, volgens SMOG, de methode waarmee de moeilijkheidsgraad van een tekst berekend wordt aan de hand van woordlengte en zinlengte (hoe langer, hoe moeilijker).
       

De SMOG-index van een tekst geeft het aantal jaar opleiding aan dat nodig is om de tekst te kunnen begrijpen. Je berekent de SMOG-index (S) met de formule:
       

       

Hierin is M het aantal woorden van drie of meer lettergrepen en Z het aantal zinnen.
Voor bovenstaand fragment geldt dat M = 14.
       

3p.

4.

Bereken de SMOG-index van de tekst in het fragment. Rond je antwoord af op een geheel getal.
   

 

Als de SMOG-index van een tekst te hoog is, kun je de tekst herschrijven. Als je bij het herschrijven van een tekst 15% minder woorden met drie of meer lettergrepen gebruikt, wordt S kleiner. Maar die verkleining van S had je ook kunnen bereiken door de tekst alleen te herschrijven in meer zinnen.
       

4p.

5.

Bereken hoeveel procent meer zinnen die nieuwe tekst moet hebben om een even grote afname in de moeilijkheidsgraad op te leveren.
   

 

Van een bepaald artikel is de SMOG-index gelijk aan 17. Als we de waarden van M en Z willen variëren zonder dat daarbij de SMOG-index verandert, dan is er een recht evenredig verband tussen M en Z, oftewel: M = p • Z
       

5p.

6.

Bereken de waarde van p in één decimaal nauwkeurig voor het geval dat S = 17.
   

 

Door een tekst te herschrijven in een tekst met meer zinnen, kun je S kleiner maken. Als we ervan uitgaan dat van een tekst het aantal woorden met drie of meer lettergrepen 75 is en blijft, dan kun je de formule van S herschrijven als

S = 1,0430 • √75 • √30 • Z -0,5  + 3,1291

en dus als

S = 49,47 • Z-0,5 + 3,1291

Die laatste formule kun je vervolgens differentiëren.
       

4p.

7.

Geef de formule van de afgeleide  dS/dZ en leg met behulp van deze afgeleide uit dat S afnemend daalt als de hoeveelheid zinnen groter wordt.
   

 

 

Buisfolie.
       

Een bedrijf produceert plastic verpakkingsmateriaal. Men maakt er onder andere buisfolie. Buisfolie wordt verwerkt tot plastic zakken. Bij de productie van de buisfoliezakken moet de breedte binnen nauwe grenzen blijven. De streefwaarde is 715 mm.
Om het risico te beperken dat de zakken te smal zijn, wordt de gemiddelde breedte ingesteld op 715,6 mm. Neem aan dat de breedte normaal verdeeld is met σ = 0,5 mm.

Bij de productie van buisfoliezakken voor een bepaalde afnemer is vastgelegd dat het tolerantiegebied het gebied is waar de breedte van de zakken maximaal 1 mm van de streefwaarde van 715 mm afwijkt.
       

3p.

8.

Bereken het percentage van de partij zakken dat buiten dit tolerantiegebied ligt.
     

 

Men vindt het productieproces voor een andere afnemer van buisfoliezakken acceptabel als hoogstens 2,5% van de zakken breder is dan 716 mm. Hiervoor moet de standaardafwijking wel veranderen. Het is mogelijk de machine zo in te stellen dat de gemiddelde breedte niet verandert maar de standaardafwijking wel.
       

2p.

9.

Beredeneer of de standaardafwijking dan kleiner of groter dan 0,5 moet zijn.
     

 

De bedrijfsleiding streeft naar een weekproductie van 26 000 kg buisfolie.
In 2013 beweerden de technici van het bedrijf dat in 2014 voor elk van de 48 gewone werkweken de kans minstens 75% zou zijn dat die weekproductie van 26 000 kg (of meer) gerealiseerd kon worden.

Later bleek echter dat die weekproductie van 26 000 kg (of meer) in 2014 slechts in 27 van de 48 gewone werkweken gehaald was.
       

6p.

10.

Onderzoek met behulp van een hypothesetoets of er reden is om de bewering van de technici in twijfel te trekken. Neem daarbij een significantieniveau van 1%.
     

 

Bij het bedrijf komt het verzoek binnen om een spoedorder te verwerken van 23750 kg buisfolie. Deze bestelling moet binnen een week geleverd worden.

Op basis van eerdere gegevens gaat de leiding ervan uit dat het gewicht in kg van de buisfolie die per week geproduceerd wordt normaal verdeeld is met μ = 28000 en σ = 3300.
       

3p.

11.

Toon hiermee aan dat de kans dat het bedrijf de weekproductie van 23750 kg niet haalt ongeveer 9,9% is.
     

 

Er bestaat dus een kans van 9,9% dat het bedrijf de weekproductie niet haalt. Het bedrijf kan zodoende met 90,1% zekerheid de spoedorder uitvoeren.
Voor die spoedorder van 23750 kg buisfolie wordt een prijs van €2,15 per kg gerekend als deze binnen die week geleverd wordt. Als dit echter niet lukt dan haakt de klant af en kan het bedrijf een boete van €50000,- verwachten. De partij buisfolie kan dan nog wel te zijner tijd afgemaakt worden en aan een andere klant worden verkocht voor €0,50 per kg. Het is nu de taak van het management om de risico’s af te wegen en een keuze te maken of men deze spoedorder al dan niet zal accepteren.
       

4p.

12.

Bereken de verwachtingswaarde van de opbrengst voor het bedrijf als men deze spoedorder accepteert.
     

 

 

Tarwe.
       

Tarwe is één van de belangrijkste granen. Van tarwe wordt bloem gemalen en brood gemaakt. Aan het begin van iedere week wordt op de groothandelsbeurs van Rotterdam de actuele marktprijs van tarwe (in euro per 1000 kg) bekendgemaakt. Op de site productschapakkerbouw.nl zijn voor de eerste weken van 2014 deze marktprijzen door middel van stippen in een figuur gezet. De stippen zijn met lijnstukjes verbonden. Zie onderstaande figuur.
       

       

In de figuur zie je dat de marktprijs van week 3 naar week 4 gedaald is. Ook van week 13 naar week 14 is een daling te zien.
       

3p.

13.

Beredeneer, zonder berekening, in welk van beide perioden de procentuele daling van de marktprijs van tarwe het grootst is.
     

 

Er is een verband tussen de vraag naar tarwe en de prijs van tarwe. In het boek ‘Wiskunde voor economie’ wordt daarvoor de volgende prijs-vraag-formule vermeld:

       

Hierin is p de prijs in euro per 1000 kg en q de vraag in 1000 kg per maand.
       

3p.

14.

Bereken de grootste gehele waarde van q waarvoor deze prijs-vraag-formule nog betekenis heeft.
     

 

Op een bepaald moment wordt tarwe verhandeld voor 232 euro per 1000 kg.
       

4p.

15.

Bereken, uitgaande van de formule, met hoeveel kg per maand de vraag afneemt als de prijs toeneemt van 232 euro per 1000 kg naar 238 euro per 1000 kg. Rond je antwoord af op tientallen kilo’s.
     

 
Voor de totale maandopbrengst van tarwe TO geldt de formule:

       

3p.

16.

De eenheid van TO is euro per maand. Toon dit aan en bereken bij q = 100 de totale maandopbrengst.
     

 
De afgeleide van TO is:

       

4p.

17.

Onderzoek met behulp van   dTO/dq  of TO een maximum heeft.
     

 

 

Prille groei
       

Gemiddeld duurt een zwangerschap bij de mens 38 weken. Een ongeboren kind van 8 weken of ouder wordt een foetus genoemd.
In de volgende tabel staat het (gemiddelde) lichaamsgewicht G in gram van een foetus bij een leeftijd van t weken.
       
Leeftijd t in weken Lichaamsgewicht G in gram
8 4,7
10 21
15 160
20 480
25 990
30 1700
35 2700
38 3500
       

In deze opgave willen we onderzoeken welk model er bij deze tabel zou kunnen passen.
Het eerste model dat we bekijken is dat van exponentiële groei:

G = b • at  met a en b constanten.

Veronderstel dat de groei tussen week 8 en week 10 inderdaad exponentieel verloopt.
       

3p.

18.

Bereken met hoeveel procent per week het gewicht van de foetus dan toeneemt in die periode.
     

 

Exponentiële groei is echter geen goed model voor de groei van de foetus in de gehele periode van 8 tot 38 weken. Dit kun je afleiden uit de tabel.
       

3p.

19.

 Laat dat met een berekening zien.
     

 

Om een beter model voor de groei van de foetus te maken, berekenen we de logaritmes van de getallen in de vorige tabel.
We bekijken dus de waarden van M = log (G) ten opzichte van L = log (t) . Zie de volgende tabel en de bijbehorende punten in de figuur ernaast.
       

       

De punten in de figuur liggen bij benadering op een bergparabool. Deze parabool is in de figuur getekend. Bij deze parabool hoort de volgende formule:

M = −7,131+11,305 • L − 2,892 • L2

Het gewicht van een foetus van 30 weken kan met deze formule worden berekend: bij t = 30 hoort L = log(30) ≈1,48 . Met de formule kun je de waarde van M en daarna de bijbehorende waarde van G berekenen.
Die waarde wijkt af van de waarde volgens de eerste tabel uit deze opgave.
       

3p.

20.

 Bereken hoeveel deze afwijking bedraagt.
     

 

Als de parabool van de figuur de groei goed beschrijft, dan zou de grafiek moeten stijgen gedurende de hele zwangerschap.
       

4p.

21.

Bereken met behulp van de afgeleide functie M' de waarde van t waar de grafiek van M weer gaat dalen en leg uit dat dit voor het model geen bezwaar is.
     

 

Voor een foetus van 20 weken en ouder blijkt een rechte lijn nog beter bij de punten in de figuur te passen dan de parabool van zojuist. Deze lijn is in onderstaande figuur getekend.
       

       

De vergelijking van deze lijn is:

M = −1,314 + 3,075 • L

Omdat geldt M = log (G) en L = log (t) is deze vergelijking te schrijven als

log(G) = −1,314 + 3,075 • log(t)   (formule 1)

Deze formule 1 is te herschrijven tot formule 2:

G = 0,0485 • t3,075  (formule 2)
       

4p.

22.

Laat zien hoe je formule 1 kunt herleiden tot formule 2 of hoe je formule 2 kunt herleiden tot formule 1.
     

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
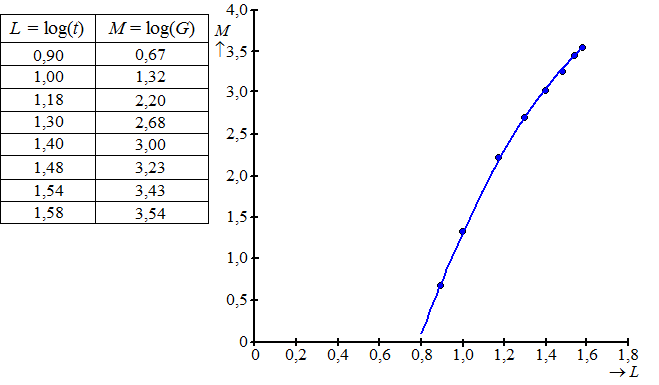
1. In de tabel staan 354 hittegolfdagen
De periode 1911 - 2013 bestaat uit 103 jaar van 365 dagen, dus dat zijn 37595 dagen.
De kans is dan  354/37595 = 0,0094 dus dat is 0,9%
Het is inderdaad ongeveer gelijk aan 1%.
   
2. invullen in de formule geeft de volgende waarden:
 
k 0 1 2 3 4
N(k) 72 27 5 1 0
aantal in de tabel 71 27 4 0 1

Het wijkt nergens meer dan één af, dus die waarden zijn er niet.
   
3.
klasse á30, 31] á31, 32] á32, 33] á33, 34] á34, 35] á35, 36] á37, 38]
aantal 1 7 14 6 7 3 1
cumulatief 1 8 22 28 35 38 39
cumulatief % 2,5 20,5 56,4 71,8 89,7 97,4 100
   
 

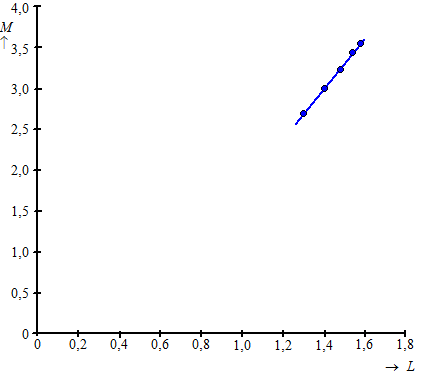
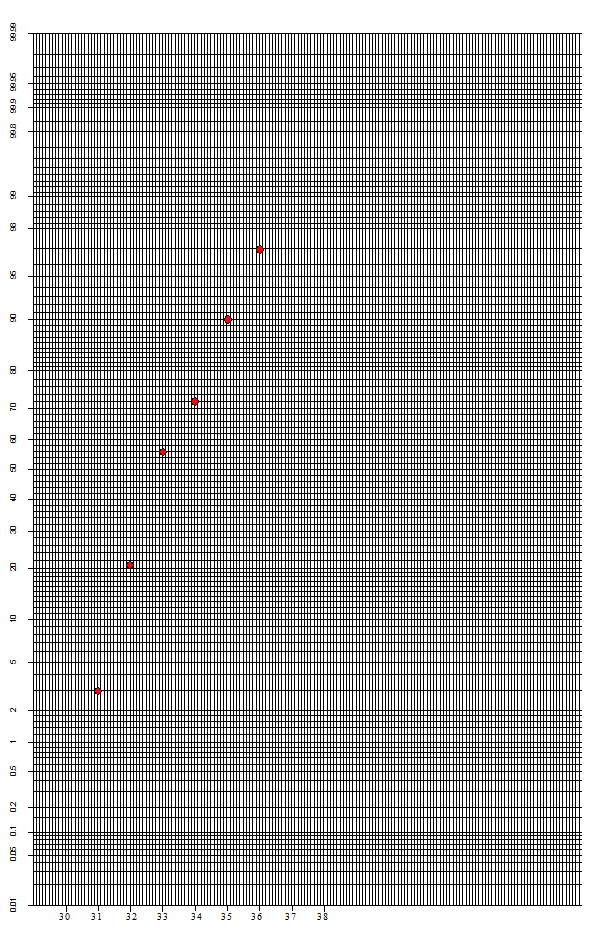
  De punten liggen redelijk op een rechte lijn dus het is ongeveer normaal verdeeld.
   
4. De tekst bestaat uit drie zinnen, dus Z = 3
S = 1,0430 • √(14 • 30/3) + 3,1291 = 1,0430 • √140 + 3,1291 = 15,47
Afgerond is S = 15
   
5. als M 15% kleiner wordt is de nieuwe M dus gelijk aan 0,85M
Dan staat er onder de wortel  0,85M • 30/Z
Als je Z verandert in X dan staat er onder de wortel   M • 30/X

Die twee moeten gelijk zijn:    0,85M • 30/Z  =   M • 30/X 
0,85/Z = 1/X    geeft   Z = 0,85X  dus  X = 1/0,85 • Z = 1,18Z
Dat is dus 18% meer
   
6. 17 =  1,0430 • √(M • 30/Z) + 3,1291
13,8709 = 1,0430 • √(M • 30/Z)
13,299 = √(M • 30/Z)
176,864 = M • 30/Z  =  M/Z • 30
5,895 = M/Z
M = 5,9Z
   
7. S' = -0,5 • 49,47Z-1,5 
S' = -24,735 • Z-1,5
S' = -24,735/Z1,5

Omdat Z > 0  is dit altijd negatief dus is S dalend.
Als Z groter wordt, dan wordt Z1,5 ook groter dus wordt S' kleiner (negatief), en dat betekent dat de daling afneemt, dus dat S afnemend dalend is.
   
8. 1 mm afwijking betekent een waarde tussen 714 en 716
binnen het interval:  normalcdf(714, 716, 715.6, 0.5) = 0,7875
buiten het interval  1 - 0,7875 = 0,2125  dus dat is  21,25%
   
9. Als de standaardafwijking kleiner wordt, liggen er meer waarden dichter bij het gemiddelde 715,6.
Dat moet ook, dus moet de standaardafwijking kleiner worden.
   
10. H0:  p = 0,75
H1:  p < 0,75
De meting was 27 van de 48
Overschrijdingskans:   P(X ≤ 27)  met n = 48 en p = 0,75
P(X ≥ 27)  = binomcdf(48, 0.75, 26) = 0,0014
Dat is minder dan 0,01 dus H0 mag worden verworpen
Er is dus WEL reden om de bewering van de technici in twijfel te trekken.
   
11. Het wordt niet gehaald als de productie kleiner is dan 23750 kg.
normalcdf(0, 23750, 28000, 3300) = 0,09889
Dat is 9,889% dus dat is inderdaad ongeveer 9,9%
   
12. Als het wel lukt is de opbrengst 2,15 • 23750 = 51062,50  met kans  0,901
Als het niet lukt is de opbrengst 0,50 • 23750 - 50000 = -38125  met kans 0,099

De verwachtingswaarde is  51062,50 • 0,901 - 0,099 • 38125 = €42232,94
   
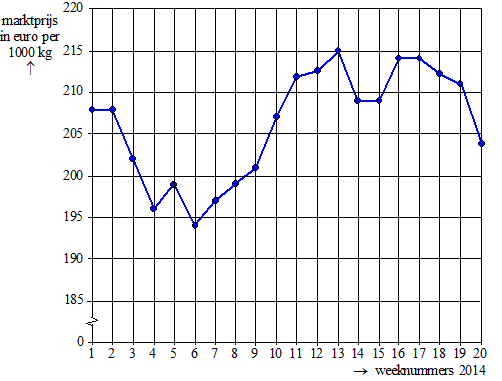
13. De daling is in beide perioden gelijk want de lijntjes lopen even steil omlaag
Maar dan is dat in procenten tussen week 3 en 4 in procenten groter want daar is de marktprijs lager.
   
14. De formule heeft betekenis zolang het deel onder de wortel groter dan nul is.
-23q + 3800 = 0
23q = 3800
q = 165,22
   
15. 232 = 10√(-23q + 3800)
23,2 = √(-23q + 3800)
538,24 = -23q + 3800
23q = 3261,76
q = 141,8157

238 = 10√(-23q + 3800)
23,8 = √(-23q + 3800)
566,44 = -23q + 3800
23q = 3233,56
q = 140,5896

Dat is een afname van 1,2261 duizend kilo, dus ongeveer 1230 kg 
   
16. De eenheid van p is  euro/1000 kg
De eenheid van q is  1000 kg/maand
De eenheid van p • q  is   euro/1000 kg • 1000 kg/maand  =  euro/maand.  
q = 100 geeft  TO = 10 • Ö(-23 • 100 + 3800) • 100  =  10 • Ö1500 • 100 = 38729,83  euro/maand
   
17. Voor een maximum moet  dTO/dq gelijk zijn aan nul.
 
  vermenigvuldig met √(-23q + 3800):     10(-23q + 3800) - 115q = 0
-230q + 38000 - 115q = 0
345q = 38000
q = 110,14
(het mag ook met de  via calc - ZERO)
voor q < 110 is  dTO/dq groter dan nul en voor q > 110 is dTO/dq kleiner dan nul.
De grafiek van TO gaat bij q = 110 dus van stijgend naar dalend dus heeft daar een maximum.
   
18. in twee weken is de groeifactor  21/4,7 = 4,468
voor de g per week geldt dus  g2 = 4,468  dus  g = 4,4680,5 = 2,11
dat is een toename van 111% per week
   
19. bijvoorbeeld:
tussen week 10 en 15 is de groeifactor  160/21 = 7,62
tussen week 30 en 35 is de groeifactor 2700/1700 = 1,59
Dat is niet gelijk, terwijl de tijdsverschillen wel gelijk zijn (5 weken) dus de groei is niet exponentieel.
   
20. L = 1,48 geeft  M = -7,131 + 11,305 • 1,48 - 2,892 • 1,482 = 3,27
log(G) = 3,27 geeft  G = 103,27 = 1862 gram
In de tabel staat 1700 gram dus dat scheelt 162 gram.
   
21. de grafiek gaat weer dalen als M' = 0
M' =  11,305 - 5,784 • L = 0
5,784L =  11,305
L = 1,95
Dan is  log(t) = 1,95  dus  t = 101,95 ≈ 89  weken.
Maar zo lang duurt een zwangerschap nooit.
   
22. van 1 naar 2:
log(G)( = -1,314 + 3,075  log(t)
10log(G) = 10-1,314 + 3,075log(t)
G = 10-1,314 • 103,075log(t)
G = 0,0485 • (10log(t))3,075 
G =  0,0485 • t3,075  

van 2 naar 1:
G = 0,0485 • t3,075
log(G) = log(0,0485 • t3,075)
log(G) = log(0,0485) + log(t3,075)
log(G) = -1,314 + 3,075 • log(t)