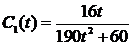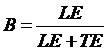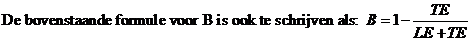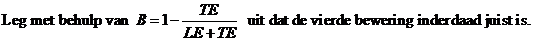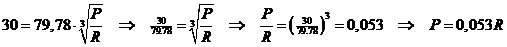| Schroefas. | |||
|
Een belangrijk onderdeel van een boot is de schroefas. Deze as wordt door de motor in beweging gebracht. Daardoor gaat de schroef van het schip draaien en dan kan de boot varen. De motor, de schroefas en de schroef samen noemen we hier het aandrijfsysteem van de boot. |
|||
|
|
|||
|
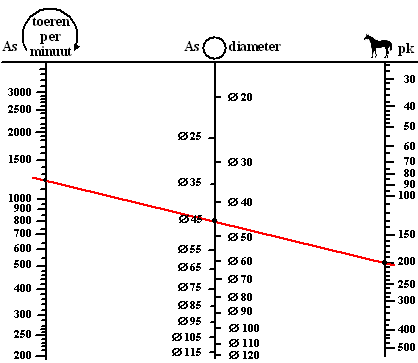
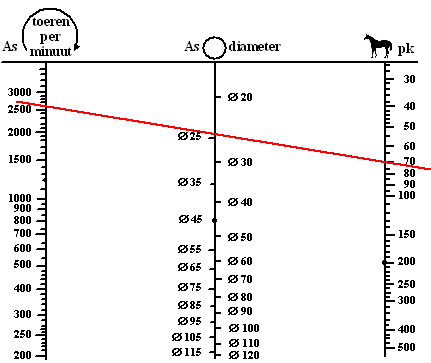
De minimale diameter van de schroefas die nodig is, hangt af van de prestaties die de motor van deze boot kan leveren. In onderstaande figuur zie je een grafiek om de minimale diameter van de as vast te stellen. In dit zogenoemde nomogram zie je drie schalen: • de middelste schaal: de diameter van de schroefas, gemeten in mm; • de rechterschaal: het vermogen, uitgedrukt in paardenkracht (pk). Zoals je kunt zien, is elk van de drie schalen niet-lineair. |
|||
|
|
|||
|
Wanneer je een lijn trekt door de drie schalen kun je een van de drie waarden bepalen als je de andere twee weet. Zo hoort volgens de figuur bij een motor van 200 pk en 1200 tpm een asdiameter van (ten minste) 45 mm. Python-Drive is een bedrijf dat aandrijfsystemen maakt. Op hun website staat dat alle systemen van het type P60-K (70 pk, 2600 tpm) een asdiameter hebben tussen 30 en 40 mm. |
|||
| 3p. | 1. |
Onderzoek met behulp van de figuur of de asdiameter van dit type groot genoeg is. |
|
|
In het voorbeeld in de figuur zie je een motor van 200 pk en 1200 tpm met een bijbehorende asdiameter van 45 mm. Er zijn ook wel motoren te vinden met een ander vermogen en een ander toerental waarbij dezelfde asdiameter van 45 mm hoort. Dan valt op dat een groter vermogen een hoger toerental oplevert. |
|||
| 3p. | 2. | Leg uit hoe je dat in de figuur kunt zien. | |
|
Lloyd’s is een organisatie die zich bezighoudt met het opstellen van regels voor de controle op de zeewaardigheid van schepen. Volgens een van deze regels moet de diameter D van de schroefas voldoen aan de volgende formule: |
|||
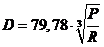 |
|||
|
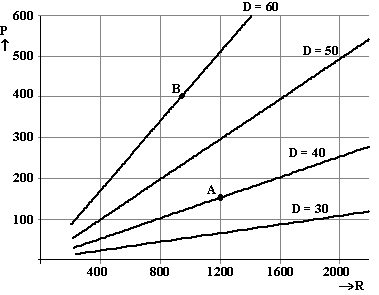
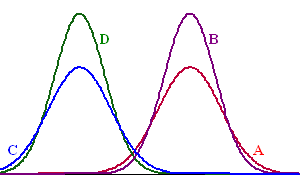
In deze formule is D uitgedrukt in mm, het vermogen P uitgedrukt in pk en het toerental R in tpm.In een tijdschrift dat gaat over aandrijfsystemen kun je onderstaande figuur tegenkomen. In deze figuur zie je voor enkele waarden van D het verband getekend tussen de bijbehorende waarden van P en R. |
|||
|
|
|||
|
In zo’n figuur kan elk aandrijfsysteem met een punt worden weergegeven. Zo hoort het punt A bij het aandrijfsysteem met waarden (1200, 150, 40).In deze figuur is punt B aangegeven. Bij dit aandrijfsysteem is het vermogen goed af te lezen. De waarde van het toerental is echter niet nauwkeurig af te lezen, maar met behulp van de formule kunnen we deze wel berekenen. |
|||
| 4p. | 3. |
Bereken met behulp van de formule het toerental dat bij dit aandrijfsysteem hoort. |
|
|
In enkele gevallen komt het voor dat de asdiameter al bekend is, bijvoorbeeld wanneer alleen de motor moet worden vervangen. We gaan uit van een asdiameter van 30 mm. |
|||
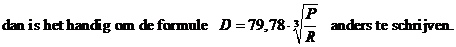 |
|||
| 4p. | 4. |
Herschrijf de formule hierboven zo dat je een formule krijgt waarin P uitgedrukt wordt in R. |
|