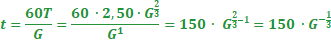Nieuwe pagina 1

VWO WA12, 2010 - I Bezem.

Marathonloopsters

De Olympische hardloopwedstrijd met de grootste lengte is de marathon: ruim 42 kilometer, om precies te zijn 42195 meter. De marathon wordt zowel door mannen als door vrouwen gelopen. In deze opgave concentreren we ons op de marathonloopsters. De prestatie van een loopster geeft men in krantenberichten meestal weer door de tijd waarin de marathon is afgelegd, maar een even duidelijke maat is de gemiddelde snelheid over het gehele parcours. Dit noemen we kortweg de snelheid. Deze snelheid drukken we uit in m/s (meters per seconde). Een marathonloopster legt de marathon af in 2 uur, 43 minuten en 32 seconden.

3p.	1.	Bereken haar snelheid in m/s.

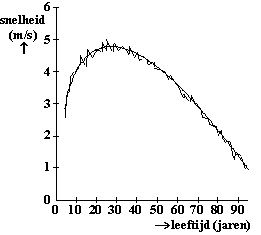
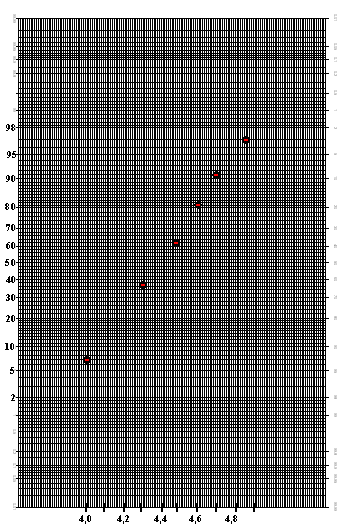
Elmer Sterken van de Rijksuniversiteit Groningen heeft onderzoek gedaan naar het verband tussen de snelheid van Amerikaanse marathonloopsters en hun leeftijden. De figuur hieronder is afkomstig uit het rapport dat hij daarover geschreven heeft. In onderstaande figuur is voor iedere leeftijd weergegeven de hoogste snelheid ooit gelopen door een Amerikaanse (zie de ‘zigzaglijn’). De geregistreerde leeftijden lopen van 6 tot en met 90 jaar1).



	noot 1: Deze figuur is ontstaan door allerlei gegevens van verschillende loopafstanden (op verantwoorde manier) om te zetten naar de marathonlengte. Hierdoor zijn in deze figuur ook voor een marathon onwaarschijnlijk jonge leeftijden vermeld.

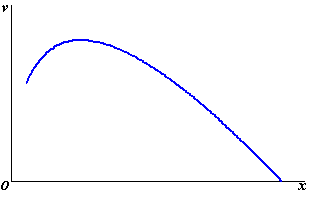
De ‘zigzaglijn’ is in deze figuur benaderd door de grafiek met de formule: v = 2,836 • x^0,665 −1,390• x^0,818 Hierin is v de hoogste snelheid in m/s van marathonloopsters met een leeftijd van x jaar. In de figuur hieronder is de grafiek van v weergegeven.



In het vervolg van deze opgave beschouwen we deze laatste grafiek en de formule voor v als een wiskundig model van de werkelijkheid. Petra loopt vaker een marathon en hoopt binnenkort de marathon binnen 3 uur te volbrengen. Petra is 52 jaar.

3p.	2.	Kan een 52-jarige marathonloopster volgens dit model de marathon binnen 3 uur lopen? Licht je antwoord toe.

De grafiek van v heeft een maximum. Volgens het model is er dus blijkbaar een leeftijd waarop marathonloopsters (gemiddeld) het beste presteren.

5p.	3.	Stel de afgeleide van v op en bereken hiermee deze leeftijd.

Stoppen met roken.

Veel mensen beginnen op jonge leeftijd met roken en proberen daar op latere leeftijd weer mee op te houden. Dat lukt niet altijd.
Het Centraal Bureau voor de Statistiek (CBS) publiceert regelmatig cijfers waarmee het rookgedrag van Nederlanders kan worden bestudeerd. In de volgende tabel vind je enkele getallen.

rokers en aantallen sigaretten
jaar	2001	2005
aantal Nederlanders, in miljoenen	16,0	16,3
percentage rokers	33,3%	29,5%
gemiddeld aantal sigaretten per roker per jaar	4526	4271

4p.

Bereken met hoeveel procent het totale aantal gerookte sigaretten in 2005 is afgenomen ten opzichte van 2001.

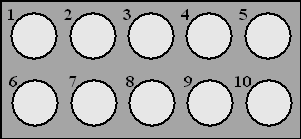
Er zijn veel hulpmiddelen om minder te gaan roken of er zelfs helemaal mee te stoppen. Eén daarvan is het gebruik van tabletten van het merk Fumostop.
Om na te gaan of Fumostop een middel is dat inderdaad helpt, wordt het volgende onderzoek uitgevoerd.
Uit alle zware rokers wordt aselect een groep van 18 proefpersonen gekozen. Elke proefpersoon krijgt 10 tabletten die uiterlijk niet van elkaar verschillen. De tabletten zijn verpakt in doordrukstrips met bij elk tablet een nummer. Zie de figuur.

Elke proefpersoon moet 10 dagen lang iedere dag bij het opstaan één willekeurig gekozen tablet innemen, het nummer van dat tablet noteren en bijhouden hoeveel sigaretten hij die dag rookt.
Wat de proefpersonen niet weten maar de onderzoekers wel, is dat 5 van de tabletten inderdaad van het merk Fumostop zijn. De andere 5 tabletten bevatten geen enkele werkzame stof. We geven de ‘echte’ tabletten aan met F en de andere tabletten met NF. Aan de genoteerde tabletnummers kunnen de onderzoekers zien wanneer de F- en de NF-tabletten ingenomen zijn.
Nico is één van de 18 proefpersonen. De mogelijkheid bestaat dat hij om de dag een F-tablet inneemt, waarmee bedoeld wordt dat hij de ene dag een F-tablet en de andere dag een NF-tablet inneemt.

4p.

Bereken de kans dat hij om de dag een F-tablet inneemt.

De proefpersonen kiezen hun tabletten iedere dag dus volledig aselect. Het kan dus gebeuren dat een proefpersoon de eerste dag een van de tabletten met nummer 1 of nummer 2 kiest.

4p.

Bereken hoe groot de kans is dat 6 of meer proefpersonen op de eerste dag van het onderzoek een van de tabletten met nummer 1 of 2 kiezen.

De onderzoekers vermoeden dat het gebruik van F-tabletten leidt tot het roken van minder sigaretten. Om dat na te gaan, wordt van elke proefpersoon bijgehouden hoeveel sigaretten hij in totaal heeft gerookt op de vijf dagen met een F-tablet en op de vijf dagen met een NF-tablet. Het resultaat vind je in de volgende tabel.

proefpersoon	1	2	3	4	5	6	7	8	9
bij gebruik van F-tabletten	106	90	109	72	103	118	124	103	89
bij gebruik van NF-tabletten	112	108	132	92	96	120	145	129	101

proefpersoon	10	11	12	13	14	15	16	17	18
bij gebruik van F-tabletten	87	92	145	101	100	97	112	104	101
bij gebruik van NF-tabletten	104	127	138	124	121	139	100	93	118

6p.

Onderzoek met behulp van een tekentoets of er voldoende aanleiding is om het vermoeden van de onderzoekers te bevestigen. Neem hierbij als significantieniveau 5%.

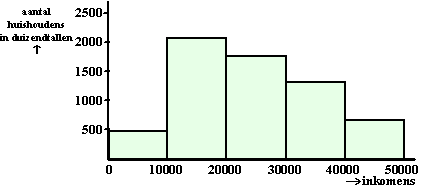
Van de mensen die in 2006 rookten, rookte 24,5% per dag 20 sigaretten of meer. Rokers rookten toen gemiddeld 11,4 sigaretten per dag. Tine wil onderzoeken of het aantal sigaretten per dag normaal verdeeld zou kunnen zijn.
Ze bedenkt de volgende aanpak: “Als er sprake is van een normale verdeling, dan kan ik de bijbehorende standaardafwijking berekenen. Daarna kan ik nagaan of die waarde – in combinatie met dat gemiddelde 11,4 – tot een conclusie leidt.”

4p.

Bereken die standaardafwijking en toon daarmee aan dat het aantal sigaretten dat een roker per dag in 2006 rookte, niet normaal verdeeld kan zijn.

Contributie.

Bij veel sportverenigingen moet je contributie betalen. Met dit geld kunnen de kosten van de vereniging betaald worden. Voorbeelden van deze kosten zijn zaalhuur en trainers.

De contributie voor een squashclub was in 1995 €180,- per jaar. De contributie wordt elk jaar met 3,5% verhoogd.
Martin is al vanaf 1 januari 1995 lid van deze squashclub.
De ontwikkeling van de contributie kun je beschrijven met een discreet model.

Een recursieve formule voor dit model is: C(t +1) = C(t) • 1,035 met C(0) =180 . Hierin is C(t) de contributie op tijdstip t met t in jaren en t = 0 in 1995.

Met een directe formule kun je de hoogte van de contributie op elk tijdstip t rechtstreeks berekenen. Je hoeft dan niet eerst de contributie van het voorgaande jaar te kennen of te berekenen.

3p.

Stel een directe formule op en bereken hoeveel contributie Martin in 2010 moet betalen aan de squashclub.

3p.

10.

Bereken hoeveel contributie Martin vanaf 1 januari 1995 tot en met 31 december 2010 in totaal heeft betaald aan de squashclub.

In 1995 bestond de squashclub uit 850 leden. Dit ledenaantal is in de loop der jaren constant gebleven.
Niet al het contributiegeld wordt direct besteed. Met een jaarbedrag van 150 euro per lid kunnen jaarlijks alle kosten van de vereniging betaald worden.
Het geld dat jaarlijks extra binnen komt, wordt gereserveerd voor een verbouwing van de kleedkamers. Dit geld wordt vanaf 1995 eerst op een spaarrekening gezet. De jaarlijkse rente is 7%. Zie de volgende tabel.

jaar	1995	1996	1997
extra bedrag per lid	€30	€36,30	€42,82
toename reserve	€25500	€30855
totaal bank inclusief rente op einde van het jaar	€25500	€58140

In 1995 betaalt elk lid dus 180 euro en wordt er 850·30 = 25500 euro op de spaarrekening gezet.
De kosten van de verbouwing van de kleedkamers worden geschat op 206000 euro.

6p.

11.

Onderzoek of de squashclub die verbouwing kan betalen met het bedrag dat in 1999 op het einde van het jaar op de spaarrekening staat.

Na de verbouwing van de kleedkamers verwacht de squashclub een lichte groei van het aantal leden. Een geschikt model dat bij deze groei past is het volgende:

L(t +1) = 2,015 • L(t) − 0,000812 • (L(t))²

Hierbij is L(0) = 850 en t = 0 in het jaar van de verbouwing.

4p.

12.

Bereken de grenswaarde van het aantal leden van de squashclub.

Klokken.

Grote klokken zoals kerkklokken worden gemaakt van brons. De kosten die gemoeid zijn met het vervaardigen van klokken hangen dus onder andere af van de prijs van het brons. In de volgende figuur zie je een grafiek van de bronsprijs door de eeuwen heen. Op de verticale as is een logaritmische schaalverdeling gebruikt.



Op de verticale as zie je de prijs van brons in stuivers per pond (1 pond is 500 gram). Eeuwen geleden was de stuiver een gangbaar betaalmiddel. Aan de grafiek in deze figuur zie je dat de prijs van brons in 2000 flink groter is dan in 1550.

3p.	13.	Bepaal aan de hand van de grafiek hoeveel keer zo groot de prijs in 2000 is als in 1550.

Bronzen klokken worden gegoten. De kosten van het gieten, de bronsprijs, het arbeidsloon, enzovoort, dragen allemaal bij aan de prijs van een klok. In de periode 1550-1600 is de prijs van een klok bij benadering exponentieel toegenomen. In 1600 was de prijs van een klok ongeveer 6 keer zo groot als in 1550. Op grond hiervan kun je een schatting maken van de prijsstijging per jaar in die periode.

4p.	14.	Bereken hoeveel procent de jaarlijkse prijsstijging bedroeg in de periode 1550-1600.

In de 17e en 18e eeuw was het gieten van een klok handwerk. Het gieten van een grote klok kost meer tijd dan het gieten van een kleine klok. Volgens een theoretisch model is er het volgende verband tussen het gewicht van een klok en de tijd die nodig is om de klok te gieten: T = c • G^2/3 Hierin is G het gewicht van de klok in ponden en T de benodigde tijd in uren. Het getal c is een constante. Alleen voor de volgende vraag nemen we c = 2,6. De bijbehorende formule is dan T = 2,6 • G^2/3

3p.	15.	Bereken hoeveel keer zo lang het duurt om een klok van 4200 pond te gieten als een klok van 700 pond.

Voor het bepalen van de waarde van de constante c moet men zich baseren op historische bronnen. In een van die bronnen wordt verteld dat klokkengieter Jean Petit in 1750 voor het gieten van een klok van 5006 pond én een klok van 3500 pond in totaal 1340 uren nodig had. Met deze gegevens kan c worden berekend.

4p.	16.	Bereken c in drie decimalen nauwkeurig op basis van de gegevens in deze bron.

Op basis van andere bronnen heeft men uiteindelijk bepaald dat voor c de waarde 2,50 het beste past. Het verband tussen het gewicht G van de klok in ponden en de tijd T in uren is dan T = 2,50 • G^2/3 Omdat het klokkengieten zoveel tijd kost, is men ook geïnteresseerd in een formule voor de tijd per pond. We noemen de tijd per pond t. Omdat de tijd per pond t meestal minder is dan een uur, wordt deze uitgedrukt in minuten.

4p.	17.	Geef het verband tussen de tijd t (in minuten per pond) en het gewicht G (in ponden) van een klok.

Inkomen.

Het CBS (Centraal Bureau voor de Statistiek) besteedt elk jaar aandacht aan de verdeling van de inkomens van huishoudens in Nederland. In de volgende tabel is voor het jaar 2004 weergegeven hoeveel huishoudens in een bepaalde inkomensklasse zaten.

besteedbaar inkomen in euro's	aantal huishoudens in duizendtallen
0 - 10000	490
10000 - 20000	2057
20000 - 30000	1777
30000 - 40000	1309
40000 - 50000	687
50000 - 70000	460
meer dan 70000	197

Met behulp van lineair interpoleren kun je een schatting maken van het percentage huishoudens met een besteedbaar inkomen van ten hoogste 27000 euro.

5p.

18.

Schat dat percentage huishoudens met behulp van lineair interpoleren.

De verdeling van de inkomens is geen normale verdeling, zelfs niet bij benadering.
Dat kun je bijvoorbeeld zien door het histogram (Een histogram wordt ook wel staafdiagram genoemd) te tekenen voor de inkomensklassen 0 – 10000 tot en met 40000 – 50000.

4p.

19.

Teken dit histogram en leg met behulp daarvan uit dat deze frequentieverdeling niet kan worden benaderd met een normale verdeling.

Toch is er wel een manier om de tabel in verband te brengen met een normale verdeling. Dat gaat als volgt:
We geven de inkomens aan met X en berekenen van alle inkomens de logaritme. Die noemen we L, dus L = log(X ) . We krijgen dan voor L een klassenindeling met andere grenzen. Omdat log(0) niet bestaat, nemen we bij de eerste klasse als linkergrens log(1) .
Deze klassenindeling levert wel (bij benadering) een normale verdeling op.

6p.

20.

Maak de frequentieverdeling die bij L hoort en toon met behulp van normaal waarschijnlijkheidspapier aan dat deze frequentieverdeling bij benadering normaal verdeeld is (hier kun je een velletje vinden).

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

2 uur en 43 minuten en 32 seconden is 2 • 3600 + 43 • 60 + 32 = 9812 seconden
De snelheid is dan ⁴²¹⁹⁵/₉₈₁₂ = 4,3 m/s

x = 52 geeft v = 2,836 • 52^0,665 - 1,390 • 52^0,818 = 4,0376
dan is de tijd ⁴²¹⁹⁵/_4,0376 = 10451 seconden en dat is minder dan 3 uur (3 uur is 10800 seconden)
Dus het kan volgens dit model WEL.
(opm.: volgens het model kan het eigenlijk altijd wel, want het model zegt iets over gemiddelden en niets over individuen)

de afgeleide: v' = 0,665 • 2,836 • x^-0,335 - 0,818 • 1,390 • x^-0,182 =
Dat moet nul zijn voor het minimum.
Voer in de GR in Y1 = 0,665 • 2,836 • x^-0,335 - 0,818 • 1,390 • x^-0,182
Gebruik dan calc - minimum en dat levert x ≈ 27 jaar

in 2001 waren er 0,333 • 16,0 = 5,328 miljoen rokers die elk 4526 sigaretten rookten.
Dat zijn in totaal 24114,528 miljoen sigaretten

in 2005 waren er 0,295 • 16,3 = 4,8085 miljoen rokers in Nederland die elk 4271 sigaretten rookten
Dat zijn in totaal 20537,1035 miljoen sigaretten.

de afname is 24114,528 - 20537,1035 = 3577,4245 miljoen sigaretten
Dat is 3577,4245/24114,528 • 100% = 14,8%

Er zijn twee mogelijkheden:
F, NF, F, NF, F, NF, F, NF, F, NF en NF, F, NF, F, NF, F, NF, F, NF, F
De kans op beiden is gelijk, en die is ⁵/₁₀ • ⁴/₉ • ⁴/₈ • ⁴/₇ • ³/₆ • ³/₅ • ²/₄ • ²/₃ • ¹/₂ • 1 = ¹/₂₅₂
De totale kans is daarom 2 • ¹/₂₅₂ = ¹/₁₂₆ ≈ 0,008

(of: er zijn 10 nCr 5 = 252 mogelijkheden, waarvan 2 gunstig, dus de kans is ²/₂₅₂)

Voor één persoon is die kans 0,2.
Het aantal proefpersonen dat de eerste dag tablet 1 of 2 kiest is binomiaal verdeeld.
Het aantal experimenten is n = 18.
De kans op succes (1 of 2 kiezen) per keer is 0,2
Het gaat om 6 of meer successen, dus P(X ≥ 6) = 1 - P(X ≤ 5) = 1 - binomcdf(18, 0.2, 5) = 0,133

Stel p de kans dat het aantal sigaretten bij gebruik van NF-tabletten groter is dan bij gebruik van F-tabletten.
H₀: er is geen verschil, p = 0,5
H₁: bij F-tabletten minder, p > 0,5
De tabel geeft in 14 van de 18 gevallen en lager aantal
De overschrijdingskans is P(X ³ 14) met de binomiale verdeling n = 18 en p = 0,5
P(X ≥ 14) = 1 - P(X ≤ 13) = 1 - binomcdf(18, 0.5, 13) = 0,01544
Dat is minder dan 5% dus H0 moet worden verworpen.
Er is dus WEL voldoende aanleiding om het vermoeden van de onderzoekers te bevestigen.

20 of meer betekent in de klokvorm de oppervlakte vanaf 19,5. (continuïteitscorrectie)
normalcdf(19,5, 10000..., 11.4, X) = 0,245
voer in de GR in: Y1 = normalcdf(19,5, 100000, 11.4, X) en Y2 = 0,245
intersect geeft X = σ = 11,7
Als het gemiddelde 11,4 is, dan kan de standaardafwijking nooit 11,7 zijn, want dat zou betekenen dat een aantal rokers minder dan nul sigaretten per dag zou roken!
Daarom zal het aantal sigaretten niet normaal verdeeld zijn.

Omdat C elke keer met 1,035 (een constant getal) wordt vermenigvuldigd is de directe formule een exponentiële formule met groeifactor 1,035.
De beginwaarde is 180 dus dat geeft de formule C(t) = 180 • 1,035^t
In 2010 is t = 15 dus C = 180 • 1,035¹⁵ = €301,56

10.

C(0) + C(1) + C(2) + .... + C(15)
Som van een meetkundige rij: ^{(volgende - eerste)}/_{(reden
-1)}
C(16) = 180 • 1,035¹⁶ = 312,12
Som = ^{(312,12 - 180)}/_{(1,035 - 1)} = €3774,86

11.

jaar	1995	1996	1997	1998	1999
contributie	€180	€186,30	€192,82	€199,57	€206,55
extra bedrag per lid	€30	€36,30	€42,82	€49,57	€56,55
toename reserve	€25500	€30855	€36397	€42134,5	€48067,5
totaal bank inclusief rente op einde van het jaar	€25500	€58140	€98606,80	€147643,78	€206046,34

Die laatste rij krijg je door 1,07 • het bedrag links ervan + het bedrag erboven
Dus JA; de club kan het betalen.

12.

Voor de grenswaarde geldt: G = L(t) = L(t + 1)
Dus G = 2,015 • G − 0,000812 • G²0,000812G² - 1,015G = 0
G(0,000812G - 1,015) = 0
G = 0 ∨ 0,000812G- 1,015 = 0
G = ^1,015/_0,000812 = 1250

13.

Aflezen in 1550: ongeveer 2,3 stuivers per pond
Aflezen in 2000: ongeveer 70 stuivers per pond
Dat is ongeveer ⁷⁰/_2,3 = 30 keer zo groot.

14.

in 50 jaar groeit het met een factor 6.
Dat betekent dat g⁵⁰ = 6
Dan is g = 6^1/50 = 1,0365
Dat is ongeveer 3,6% per jaar.

15.

T = 2,6 • 700^2/3 = 204,977...
T = 2,6 • 4200^2/3 = 676,819...
De verhouding is ^676,819../_204,977... = 3,302
Het duurt ongeveer 3,3 keer zo lang.

16.

De eerste klok kost c • 5006^2/3 uren
De tweede klok kost c • 3500^2/3 uren
Sa men kost dat c • 5006^2/3 + c • 3500^2/3 uren
1340 = c • 5006^2/3 + c • 3500^2/3
1340 = c • 292,635... + c • 230,521...
1340 = c • 523,157...
c = 1340/ 523,157... = 2,561

17.

De tijd per pond is ^T/_G uren
De tijd per pond is ^T/_G • 60 = ^60T/_G minuten

18.

Het totaal aantal huishoudens is 6977 (duizend); tel de tweede kolom op.

het zijn in ieder geval alle huishoudens uit de eerste twee klassen en dat zijn er al 490 + 2057 = 2547
de klasse 20000 - 30000 heeft klassebreedte 10000
20000 - 27000 heeft breedte 7000 dus dat is ⁷/₁₀ deel daarvan
Dan zal het aantal huishoudens ook ⁷/₁₀ deel zijn: ⁷/₁₀ • 1777 = 1244 (afgerond)
In totaal zijn er dan 2547 + 1244 = 3791 duizend huishoudens onder de 27000 euro.
Dat is ³⁷⁹¹/₆₉₇₇ • 100% = 54,3%

19.

Een normale verdeling is symmetrisch dit histogram duidelijk niet. Daarom zal het geen normale verdeling zijn.

20.

Dat geeft de volgende tabel:

inkomensklasse	rechtergrens	log(L)	frequentie	cumulatieve frequentie	cum. freq. in procenten
0 - 10000	10000	4,00	490	490	7,0
10000 - 20000	20000	4,30	2057	2547	36,5
20000 - 30000	30000	4,48	1777	4324	62,0
30000 - 40000	40000	4,60	1309	5633	80,7
40000 - 50000	50000	4,70	687	6320	90,6
50000 - 70000	70000	4,85	460	6780	97,2

Op normaalpapier ziet dat er zó uit: