| VWO WA12, 2007 - I | ||
| Rijexamen | |||
|
Door het CBR (Centraal Bureau Rijvaardigheidsbewijzen) worden jaarlijks ruim 400 000 examens voor een rijbewijs voor personenauto’s afgenomen. Dit examen bestaat uit twee delen: een theorie-examen en een praktijkexamen. Je moet eerst geslaagd zijn voor het theorie-examen voordat je mag deelnemen aan het praktijkexamen.
|
|
||
| Vóór 1 oktober 2002 bestond het theorie-examen uit 50 ja/nee-vragen. Een kandidaat was geslaagd voor het theorie-examen als ten minste 45 ja/nee-vragen goed werden beantwoord. Hannie Samson wist, tijdens haar theorie-examen, van 41 ja/nee-vragen het goede antwoord. Door de overige 9 ja/nee-vragen te gokken, had Hannie Samson toch een kans om te slagen. | |||
| 5p | 5. | Bereken deze kans. Geef je antwoord in 2 decimalen nauwkeurig. | |
|
Sinds 1 oktober 2002 is het theorie-examen vernieuwd. In het nieuwe theorieexamen zitten bij de 50 vragen niet alleen ja/nee-vragen maar ook andersoortige vragen zoals open vragen en/of driekeuzevragen. Ook nu is een kandidaat geslaagd voor het theorie-examen als ten minste 45 vragen goed worden beantwoord. Herman Spiering doet een theorie-examen dat bestaat uit 40 ja/nee-vragen en 7 driekeuzevragen en 3 open vragen. Hij weet alleen het goede antwoord van 36 ja/nee-vragen en 6 driekeuzevragen. De 3 open vragen heeft hij in ieder geval fout. Van de resterende vragen moet Herman het antwoord gokken. Herman kan nog slagen voor dit examen. Dan moet hij ten minste drie van de vier resterende ja/nee-vragen goed gokken of hij moet twee van de vier resterende ja/nee-vragen én de resterende driekeuzevraag goed gokken. |
|||
| 4p | 6. |
Bereken de kans dat Herman zal slagen voor dit theorie-examen. Geef je antwoord in 2 decimalen nauwkeurig. |
|
|
Als je slaagt voor het theorie-examen mag je praktijkexamen doen. Als je zakt voor je praktijkexamen, kun je enige maanden later opnieuw praktijkexamen doen. Sommige kandidaten zakken meerdere keren voor het praktijkexamen. Het CBR houdt gegevens bij over de slaag- en zakcijfers van de kandidaten die opgaan voor het rijexamen. Uit de gegevens van het CBR blijkt dat een kandidaat steeds dezelfde kans heeft om te slagen voor het praktijkexamen. Hierbij speelt het dus geen rol of die kandidaat voor de eerste keer examen doet of al één of meer keren gezakt is. Verder blijkt dat 11% van alle kandidaten na 4 keer nog steeds niet is geslaagd voor het praktijkexamen. Op basis van deze gegevens kun je nu berekenen hoe groot de kans is dat iemand de eerste keer al slaagt voor het praktijkexamen. |
|||
| 4p | 7. | Bereken deze kans. Geef je antwoord in 2 decimalen nauwkeurig. | |
|
Bij het CBR bestaat het rijexamen voor de motor ook uit een theorie-examen en een praktijkexamen. Volgens de gegevens van het CBR slaagt landelijk 65,5% van alle kandidaten bij de eerste keer voor het praktijkexamen voor de motor. Onlangs is een rijschool gestart die gespecialiseerd is in motorrijlessen. Van de eerste 20 cursisten die de rijschool heeft opgeleid, zijn er 17 de eerste keer geslaagd voor hun praktijkexamen. De rijschoolhouder vraagt zich af of dit een significant beter resultaat is dan het landelijke slagingspercentage |
|||
| 6p | 8. |
Onderzoek of de rijschoolhouder mag concluderen dat zijn rijschool een significant beter resultaat heeft behaald, vergeleken met het landelijke cijfer. Gebruik daarbij een significantieniveau van 1%. |
|
| Gevoelstemperatuur | |||
|
Wanneer de temperatuur buiten 19 °C is en er geen wind staat, dan ervaren we dat als een lekkere temperatuur. Als er echter bij een temperatuur van 19 °C een flinke wind staat, dan vinden we het helemaal niet meer behaaglijk. Door de wind koelt het lichaam sneller af waardoor je het gevoel krijgt dat het kouder is dan in werkelijkheid: de gevoelstemperatuur is in dat geval lager dan de werkelijke temperatuur. De gevoelstemperatuur wordt lager naarmate de windsnelheid toeneemt. In deze opgave bekijken we een tweetal modellen waarbij de gevoelstemperatuur wordt bepaald aan de hand van de werkelijke temperatuur en de windsnelheid. Het ene model is in 1948 gemaakt door de meteoroloog Court. De formule die bij dit model hoort is als volgt: |
|||
|
|||
|
In deze formule is GC de gevoelstemperatuur in °C, T de werkelijke temperatuur in °C en w de windsnelheid in m/s. De formule is geldig voor windsnelheden groter dan 1,8 m/s en voor werkelijke temperaturen beneden 33 °C. Bij een werkelijke temperatuur van 20 °C en een windsnelheid van 12 m/s hoort een bepaalde gevoelstemperatuur. Die gevoelstemperatuur is gelijk aan de gevoelstemperatuur die hoort bij een werkelijke temperatuur van 16 °C en een lagere windsnelheid. |
|||
| 5p | 9. | Bereken die lagere windsnelheid. | |
|
Het model van Court is niet het eerste model in formulevorm. In 1945 maakten de wetenschappers Siple en Passel al een ander model. Bij hun model hoort de volgende formule: |
|||
|
|||
|
Hierin is GS&P de gevoelstemperatuur in °C volgens het model van Siple en Passel; de betekenis van de overige letters is hetzelfde als bij de formule van Court. Ook de formule van Siple en Passel is geldig voor windsnelheden groter dan 1,8 m/s en temperaturen beneden 33 °C. We willen weten in hoeverre de formule van Court nu eigenlijk verschilt van die van Siple en Passel. In deze opgave beperken we dit onderzoek tot de situatie waarbij de werkelijke temperatuur 0 °C is. In dat geval wordt het verband tussen de windsnelheid en gevoelstemperatuur volgens Siple en Passel gegeven door: |
|||
|
|||
|
Volgens Court wordt in dat geval het verband tussen de windsnelheid en de gevoelstemperatuur gegeven door: |
|||
|
|||
|
Om een indruk te krijgen zijn in de figuur hieronder de grafieken afgebeeld die bij deze formules horen. |
|||
|
|
|||
|
Je kunt zien dat de formule van Siple en Passel en de formule van Court voor windsnelheden kleiner dan 6 m/s ongeveer dezelfde gevoelstemperatuur opleveren. |
|||
| 3p | 10. |
Bereken bij welke windsnelheid de laatste twee formules precies dezelfde gevoelstemperatuur geven. Geef je antwoord in twee decimalen nauwkeurig. |
|
|
Je kunt in de figuur hierboven aan de vorm van de grafiek van de formule van Court zien dat deze formule boven een bepaalde windsnelheid niet meer realistisch kan zijn. |
|||
| 6p | 11. |
Bereken met behulp van de afgeleide functie vanaf welke windsnelheid de formule van Court (bij een temperatuur van 0 °C) in elk geval niet meer realistisch is. Geef je antwoord in twee decimalen nauwkeurig. |
|
| Honingbijen | |||||
|
Biologen verrichten veel onderzoek bij diverse diersoorten. Vaak maken zij gebruik van wiskundige modellen om het gedrag van de betreffende diersoort te beschrijven. Daarover gaat deze opgave. Dansende
bijen |
|||||
|
|
|||||
|
Honingbijen geven elkaar informatie over de afstand tot de voedselbron door zogenoemde kwispeldansen uit te voeren. Het aantal kwispeldansen dat een honingbij per minuut maakt is een maat voor de afstand. Voor afstanden tussen de 300 en 2700 meter geldt ruwweg de volgende formule:
Hierin is x de afstand tot de voedselbron in kilometers en y het aantal kwispeldansen per minuut. Een honingbij die een nieuwe voedselbron heeft ontdekt, maakt 16 kwispeldansen per minuut. |
|||||
| 3p | 12. | Bereken de afstand tot deze voedselbron in meters nauwkeurig. | |||
|
Een honingbij heeft een voedselbron ontdekt en maakt kwispeldansen om andere honingbijen te informeren over de afstand. Een andere honingbij heeft een andere voedselbron ontdekt die 1 kilometer dichterbij is. Deze honingbij maakt per minuut 40% meer kwispeldansen dan de eerste honingbij. Met behulp van de formule kun je berekenen om welke twee afstanden het hier gaat. |
|||||
| 5p | 13. | Bereken deze twee afstanden. | |||
|
Tastende bijen Na 5
minuten wordt het voorwerp weer teruggeplaatst: de 1e
conditionering.
Hierin is P(n) het percentage bijen dat tijdens de n-de conditionering een strekbeweging maakt. |
|||||
| 4p | 14. |
Bereken met de recurrente betrekking hoeveel procent van de honingbijen tijdens de 5e conditionering een strekbeweging maakt. |
|||
|
Uit experimenten blijkt dat lang niet alle bijen de strekbeweging zullen gaan maken. Daarom zal de bovenstaande recurrente betrekking een grenswaarde moeten hebben die kleiner is dan 100. |
|||||
| 4p | 15. |
Onderzoek of dit zo is door de grenswaarde van de recurrente betrekking te berekenen. |
|||
|
Nadat de bijen aan 15 conditioneringen zijn onderworpen, wordt het experiment vervolgd met conditioneringen zonder beloning. De aangeleerde neiging om een strekbeweging te maken, neemt dan af. Deze afname tijdens de conditioneringen zonder beloning (dus voor n = 16, 17, 18, enzovoort) blijkt exponentieel te verlopen en wel zodanig dat per 7 conditioneringen het aantal bijen dat nog reageert met een strekbeweging halveert. Dit betekent dat het verloop van het percentage honingbijen dat nog een strekbeweging maakt, geschreven kan worden in de vorm van een recurrente betrekking: P(n + 1) = a • P(n) met n ≥ 16. Hierin is a een constant (dus vast) getal. |
|||||
| 4p | 16. | Bereken a in twee decimalen nauwkeurig. | |||
| IQ | ||
|
Een maat voor iemands intelligentie is het zogenaamde IQ (Intelligentie Quotiënt). Hoe intelligenter een persoon is, hoe hoger zijn/haar IQ is. Het IQ is bij benadering normaal verdeeld. In deze opgave nemen we aan dat het IQ van een Nederlander normaal verdeeld is met een gemiddelde waarde van 100 en een standaardafwijking van 15.
|
||
|
Van een groot aantal mensen in 25 verschillende beroepsgroepen is het IQ gemeten. Voor elke beroepsgroep is vervolgens het gemiddelde IQ en de standaardafwijking bepaald. Deze waarden zijn uitgezet met stippen in de grafiek van de figuur hieronder. Bij elke beroepsgroep hoort dus een stip. |
||
|
|
||
|
We nemen aan dat binnen elke beroepsgroep het IQ van een persoon uit die beroepsgroep normaal verdeeld is. In de figuur hierboven is duidelijk te zien dat naarmate het gemiddelde IQ van een beroepsgroep groter is, de standaardafwijking kleiner is. Door de puntenwolk in de grafiek van deze figuur kan een zo goed mogelijk passende rechte lijn worden getrokken. De formule voor deze lijn luidt: s = 45,5 – 0,272 • m. Hierin is s de standaardafwijking en m het gemiddelde IQ van een beroepsgroep. Twee beroepsgroepen blijken een gemiddeld IQ van 110,6 en 115,3 te hebben. Beide beroepsgroepen zijn niet opgenomen in de figuur hierboven. We veronderstellen echter dat ook voor deze beroepsgroepen de formule van de lijn gebruikt mag worden. |
||
| 3p | 17. |
Bereken hoeveel de bijbehorende standaardafwijkingen volgens de formule van de lijn van elkaar verschillen. |
|
In het vervolg van de opgave gaan we er omwille van de eenvoud vanuit dat de formule σ = 45,5 – 0,272 • μ exact klopt voor waarden van μ tussen 80 en 140. Uitgaande van de normale verdeling kunnen we met deze formule voor elke waarde van het gemiddelde μ berekenen hoe groot de kans is dat een persoon uit een beroepsgroep met dat gemiddelde een IQ heeft dat groter is dan 80, 85, 90, …, 135, 140. Het resultaat van deze berekeningen is grafisch weergegeven in de volgende figuur:. |
||
|
|
||
|
Bij punt A lezen we af dat de kans ongeveer 0,7 is dat een persoon uit een beroepsgroep met gemiddeld IQ van 122 een IQ heeft dat groter is dan 115. Ofwel in formulevorm: P(IQ > 115) ≈ 0,7, waarbij μ = 122. Uitgaande van het verband σ = 45,5 – 0,272 • μ kunnen we deze kans nauwkeuriger berekenen. |
||
| 4p | 18. | Bereken deze kans. Geef je antwoord in 3 decimalen nauwkeurig. |
|
Uit een grote beroepsgroep met een gemiddeld IQ van 110 worden willekeurig vier personen geselecteerd. We willen de kans weten dat alle vier personen een IQ hebben dat groter is dan 120. Deze kans kun je berekenen als je de kans weet dat één willekeurig persoon uit deze beroepsgroep een IQ groter dan 120 heeft. Deze laatste kans kun je aflezen uit de figuur hierboven. |
||
| 3p | 19. |
Bereken op bovenstaande wijze de kans dat alle vier personen een IQ hebben groter dan 120. |
|
Een vuistregel van de normale verdeling zegt dat 68% van de gegevens ligt tussen de waarde μ – σ en de waarde μ + σ. Deze vuistregel zou ook in de figuur hierboven terug te vinden moeten zijn. |
||
| 5p | 20. |
Laat zien dat deze vuistregel is terug te vinden in de grafieken van de figuur hierboven Doe dit voor personen uit een beroepsgroep met een gemiddeld IQ van 120. Licht je werkwijze toe. |
| UITWERKING | |
| Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten. | |
| 1. | Tel de gezamenlijke
stemmen: 15329 + 9080 + 8751 = 33160 Het totaal aantal stemmen was 67787, en 33160 is minder dan de helft daarvan. Tel de zetels: 10 + 5 + 5 = 20 Het totaal aantal zetels was 39, en 20 is meer dan de helft daarvan. |
| 2. | De kiesdeler is aantal stemmen/aantal zetels = 67787/39 ≈ 1738,128 |
| 3. | Bekijk de partijen
die een restzetel kregen: PvdA, CDA, GroenLinks, GPV en SP PvdA: 15329/9 = 1703, CDA: 12584/8 = 1573, GroenLinks: 5150/3 = 1717, GPV: 3399/2 = 1700, SP: 1549/1 = 1549 GroenLinks heeft het grootste gemiddelde. |
| 4. | Stel dat x
mensen van PvdA overgaan naar VVD. Dan stemmen 15329 - x op de PvdA en 9080 + x op VVD. De gemiddelde worden dan (15329 - x)/10 en (9180 + x)/6 Los op: (15329 - x)/10 = (9180 + x)/6 dat geeft het grensgeval. Dat mag met de GR, maar kan ook zó: vermenigvuldig met 6 en met 10, dat geeft: 6 • (15329 - x) = 10 • (9080 + x) ⇒ 91974 - 6x = 90800 + 10x ⇒ 1174 = 16x ⇒ x = 73,375 Dus vanaf 74 mensen zou de laatste zetel bij de VVD komen. |
| 5. | Ze moet nog minstens
4 van de 9 goed hebben. Dat is binomiaal met n = 9, p = 0,5 P(X ≥ 4) = 1 - P(X ≤ 3) = 1 - binomcdf(9, 0.5, 3) ≈ 0,75 |
| 6. | P(4 ja/nee vragen
goed) = 0,54 = 0,0625 P(3 ja/nee vragen goed) = 0,53 • 0,5 • (4 nCr 3) = 0,25 P(2 ja/nee vragen goed + 1 driekeuzevraag) = 0,52 • 0,52 • (4 nCr 2) • 1/3 = 0,125 Totale kans 0,0625 + 0,25 + 0,125 = 0,4375 ≈ 0,44 |
| 7. | Stel dat de kans op
zakken gelijk is aan p De kans op vier keer zakken is dan p4 p4 = 0,11 ⇒ p = 0,111/4 ≈ 0,5759 P(slagen) = 1 - 0,5759 ≈ 0,42 |
| 8. | H0: Het
is hetzelfde als in de rest van het land: p = 0,655 H1: Het is een beter resultaat: p > 0,655 Het is een éénzijdige toets met α = 0,01 P(X ≥ 17) = 1 - P(X ≤ 16) = 1 - binomcdf(20, 0.655, 16) = 0,0488 Dat is groter dan 0,01, dus H0 mag niet verworpen worden. Dus dat is NIET een significant beter resultaat. |
| 9. | T = 20 en w =
12 geeft (invullen) GC = 14,1535 Dat geeft bij T = 16: 14,1535 = 33 + (16 - 33) • (0,550 - 0,0454 • w + 0,417 • √w) in de GR: Y1 = 14,1535 en Y2 = 33 + (16 - 33) • (0,550 - 0,0454 • X + 0,417 • √X) window bijv. Xmin = 0, Xmax = 5, Ymin = 0, Ymax = 20 intersect levert w ≈ 2,65 m/s |
| 10. | makkie: beide formules invoeren in de GR en dan intersect: w ≈ 4,22 m/s |
| 11. | De formule is niet
meer realistisch als de gevoelstemperatuur gaat stijgen terwijl de
windsnelheid toeneemt. Dat is dus vanaf het minimum van de grafiek. Dat
vinden we door te stellen afgeleide = 0. GC = 33 - 33 • (0,550 - 0,0454w + 0,417 • w0,5) GC' = -33 • (-0,0454 + 0,417 • 0,5 • w-0,5) = 0. Vanaf hier mag het met intersect van de GR. Ook kan: ⇒ -0,0454 + 0,2085 • w-0,5 = 0 ⇒ 0,2085 • w-0,5 = 0,0454 ⇒ w-0,5 = 0,2177 ⇒ w = 0,21771/-0,5 ≈ 21,09 m/s |
| 12. | 16 = 36/(x
+ 1) ⇒ 16(x + 1) = 36 ⇒ 16x + 16 = 36 ⇒ 16x = 20 ⇒ x = 20/16 = 1,25 Dat is een afstand van 1250 m. |
| 13. | Noem de bijen 1 en
2. x2 = x1 - 1 y2 = 1,4y1 
twee vergelijkingen met twee onbekenden: vul de eerste y1 in in de tweede formule: 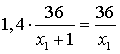
vanaf hier kan het (intersect) met de GR. Algebraïsch is natuurlijk veel leuker: breng x1 + 1 en x1 naar de andere kant: 1,4 • 36 • x1 = 36(x1 + 1) 50,4x1 = 36x1 + 36 ⇒ 14,4x1 = 36 ⇒ x1 = 2,5 km De andere afstand is dan x2 = 1,5 km |
| 14. | GR: MODE - Seq
en dan Y= nMin = 0 u(n) = 4,0 + 1,6 • u(n−1) − 0,012 • (u(n−1))2 u(nMin) = 0 TABLE levert dan P(5) = 41,342 |
| 15. | Kijk in de tabel uit
de vorige opgave bij hele grote n Dan zie je dat de waarde van P naar 56% toegaat. Dat is inderdaad kleiner dan 100% |
| 16. | Als het aantal elke
keer met factor a wordt vermenigvuldigd, dan wordt het in 7 keer
met a7 vermenigvuldigd. Dat moet dus gelijk zijn aan 0,5 want het halveert in 7 keer. a7 = 0,5 ⇒ a = 0,51/7 ≈ 0,91 |
| 17. |
σ1
= 45,5 - 0,272 • 110,6
≈ 15,417 σ2 = 45,5 - 0,272 • 115,3 ≈ 14,138 Het verschil is ongeveer 1,279 |
| 18. |
σ
= 45,5 - 0,272 • 122 = 12,316 normalcdf(115, 10000, 122, 12.316) = 0,715 |
| 19. | De kans voor één
persoon is (aflezen) ongeveer 0,26 Voor vier personen is de kans dan 0,264 = 0,005 |
| 20. |
Als m
= 120 dan is
σ = 45,5 - 0,272 • 120 = 12,86 |