VWO WISKUNDE A12, 2004 - II
APK
Auto's moeten elk jaar gekeurd worden. Deze wettelijke verplichte keuring wordt APK, Algemene Periodieke Keuring, genoemd en wordt uitgevoerd door garagebedrijven. Om na te gaan of de garagebedrijven de keuringen goed uitvoeren, voert de RDW, De Rijks Dienst voor Wegverkeer, controles uit. De RDW doet dit steekproefsgewijs.Dat wil zeggen: van alle auto's die worden gekeurd door de garagebedrijven selecteert de RDW er een aantal en onderwerpt die auto's aan een controle. Op deze wijze controleert de RDW 3% van alle gekeurde auto's.

Een garagebedrijf gaat op een dag 5 auto's keuren.
3p 1. Bereken de kans dat geen van deze 5 auto's door de RDW wordt gecontroleerd. Geef je antwoord in vier decimalen nauwkeurig.

 
Voor het beoordelen van de kwaliteit van de garagebedrijven hanteert de RDW een puntensysteem:
Ieder garagebedrijf begint met 0 punten. Als bij controle van de RDW blijkt dat de keuring van een auto niet goed is verricht, krijgt het garagebedrijf 1,5 strafpunten. Als de keuring van een auto wél goed is uitgevoerd, krijgt het garagebedrijf 0,4 bonuspunten. Straf[punten en bonuspunten worden met elkaar verrekend. Als het garagebedrijf bijvoorbeeld 0,8 bonuspunten en 1,5 strafpunten heeft gekregen, levert dit 0,7 strafpunten op. Daarmee komt het aantal punten voor dit bedrijf op -0,7.

Garagebedrijf Hendriks heeft 0 punten. Bij dit bedrijf wordt 20% van de keuringen niet goed uitgevoerd. De RDW voert vijf keer een controle bij Hendriks uit.
4p 2. Bereken de kans dat garage Hendriks na deze vijf controles meer dan nul punten heeft.
Geef je antwoord in vier decimalen nauwkeurig.

 
Met behulp van het puntensysteem van de RDW kunnen we narekenen dat bij een garagebedrijf waar 15% van de keuringen  niet goed worden uitgevoerd, elke uitgevoerde controle gemiddeld 0,115 punten oplevert. Dus acht controles door de RDW leveren zo'n bedrijf naar verwachting 0,92 punten op.
Garagebedrijf Kampman voert slechts 10% van de keuringen niet goed uit. Acht controles door de RDW zullen dit garagebedrijf naar verwachting meer punten opleveren.
Garagebedrijf Kampman heeft 0 punten.
4p 3. Bereken hoeveel punten garagebedrijf Kampman naar verwachting zal hebben nadat de acht controles zijn uitgevoerd.

 
Mede door de APK neemt de gemiddelde levensduur van personenauto's toe. In het begin van de jaren negentig van de vorige eeuwwas een personenauto na 9 à 10 jaar rijp voor de sloop. In 1998 lag de gemiddelde levensduur al een stuk hoger. Deze gemiddelde levensduur kun je berekenen met behulp van de gegevens in de onderstaande figuur. Daarin vind je in de vorm van een samengesteld staafdiagram de verdeling naar leeftijd van de personenauto's die in 1998 werden gesloopt.
4p 4. Bereken met behulp van de gegevens in deze figuur hoe groot de gemiddelde levensduur was van personenauto's op het moment van slopen.

 
Kaartspel
Een set speelkaarten bestaat uit 52 kaarten, verdeeld in de soorten schoppen (ª),  harten (©), ruiten (¨) en klaveren (§). Iedere soort bevat 13 kaarten, met de opdruk 2,3,4,5,6,7,8,9,10,boer,vrouw,heer of aas.

Het kaartspel bridge wordt gespeeld door vier spelers die ieder 13 kaarten krijgen.
We gaan er bij deze opgave van uit dat het delen van de kaarten op aselecte wijze gebeurt. Dat betekent dat bij elk spel iedere speler evenveel kans heeft op een bepaalde kaart.

 
Arie, Bert, Clemens en Douwe spelen bridge.

De kans dat Clemens bij een spel precies twee klaverenkaarten krijgt is ongeveer 0,2.
4p 5. Bereken deze kans in vier decimalen nauwkeurig.

 
Arie heeft gedurende een lange periode bijgehouden hoeveel klaverenkaarten hij bij elk spel kreeg. Het resultaat van 10000 spellen vind je in de volgende tabel.
aantal klaverenkaarten 0 1 2 3 4 5 6 7 8 9 of meer
frequentie 130 802 2060 2865 2385 1245 414 87 12 0
Het aantal van 10000 spellen is erg groot. Dat betekent dat we de uitkomsten inde tabel goed kunnen gebruiken om de theoretische kansen op de bijbehorende aantallen klaverenkaarten te benaderen.
3p 6. Gebruik de tabel om de kans te berekenen dat je in 10 spellen precies één keer géén klaverenkaarten krijgt. Rond je antwoord af op vier decimalen.

 
Douwe heeft een histogram opgesteld van de gegevens uit bovenstaande tabel. Op grond hiervan vermoedt hij dat het aantal klaverenkaarten K per spel bij benadering normaal verdeeld is.
6p 7. Zet de cumulatieve kansverdeling die volgt uit bovenstaande tabel uit op normaal waarschijnlijkheidspapier en geef je oordeel over het vermoeden van Douwe. Licht je antwoord toe.

 
Wanneer de kaarten aselect worden gedeeld, is de verwachtingswaarde van het aantal klaverenkaarten dat een speler per spel krijgt gelijk aan 3,25 en de bijbehorende standaardafwijking gelijk aan 1,365.
Veel spelcomputers gebruiken het spelprogramma 'Split' om het delen van de kaarten te simuleren. Bert vermoedt al een tijdje dat 'Split' hem te weinig klaverenkaarten geeft. Daarom houdt hij gedurende 100 spellen bij hoeveel klaverenkaarten hij krijgt. Dat blijken er in totaal 302 te zijn.
6p 8. Onderzoek of er voldoende aanleiding is om te veronderstellen dat het programma 'Split' Bert te weinig klaverenkaarten geeft. Neem als significantieniveau 5%. Je kunt hierbij gebruik maken van het feit dat het totale aantal klaverenkaarten bij 100 spellen bij benadering normaal verdeeld is.

 
Woorden Tellen
In ziekenhuizen verschijnen veel rapporten die over de behandeling van patiënten gaan. In dergelijke rapporten komen, naast het gewone taalgebruik, ook veel medische termen voor. Bij twee ziekenhuizen heeft men onderzoek gedaan naar het woordgebruik in deze rapporten. Hiervoor heeft men van 5000 rapporten geteld hoe vaak ieder woord in totaal voorkwam.
Deze rapporten bevatten samen 996734 woorden. Toch waren er in totaal slechts ongeveer 20000 verschillende woorden. Dit komt omdat er woorden zijn die heel vaak gebruikt worden. Om je hiervan een idee te geven zie je in de volgende tabel de tien woorden die het meest frequent in de rapporten werden gebruikt.
woord een de van met en het in is ik geen
frequentie 40361 36485 34231 27667 26869 22965 22082 13681 11416 11363
rangnummer 1 2 3 4 5 6 7 8 9 10
Je ziet dat in de tabel de woorden op rangnummer, in volgorde van hun frequentie, zijn genoemd. Zo kun je bijvoorbeeld aflezen dat het woord `met` in totaal 27667 keer is geteld en dat dit woord het rangnummer 4 heeft.

De onderzoekers J.B. Estoup en G.K. Zipf hebben geprobeerd in allerlei teksten een verband te vinden tussen het rangnummer r van een woord en de bijbehorende frequentie f. In 1949 vond Zipf de formule:

fr = C/r
Deze formule wordt ook wel de "wet van Zipf" genoemd.
De waarde van C hangt af van het totale aantal woorden in de tekst. Volgens Zipf is C de oplossing van de vergelijking:
2,3 • logC = aantal woorden in de tekst

De rapporten van het AZM bevatten samen 495378 woorden.
3p 9. Bereken de waarde van C die bij de rapporten van het AZM hoort. Rond af op duizendtallen.

 
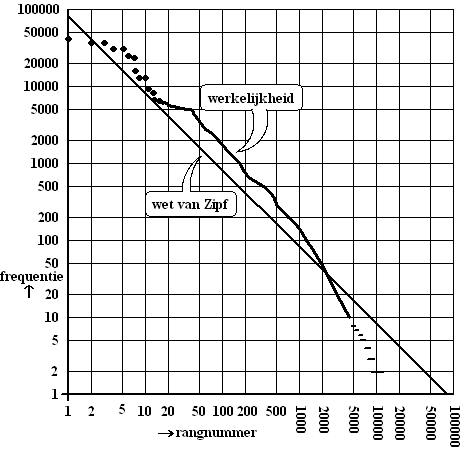
Voor de 996734 woorden in de rapporten van beide ziekenhuizen samen geldt C = 88000. In de figuur hieronder zijn van alle gebruikte woorden de frequenties uitgezet tegen de rangnummers. Op beide assen is gekozen voor een logaritmische schaalverdeling. De woorden uit de tabel hierboven vind je terug als de bovenste 10 punten.
Om de wet van Zipf en de werkelijkheid met elkaar te kunnen vergelijken is in onderstaande figuur ook de grafiek van  fr = 88000/r getekend.
De wet van Zipf geldt voor algemene teksten zoals krantenartikelen en dergelijke. Omdat medische rapporten niet "algemeen" zijn, vertonen de grafieken opmerkelijke verschillen. Tussen de rangnummers 2 en (ongeveer) 2200 zijn de werkelijke frequenties groter dan de frequenties volgens de wet van Zipf.
4p 10. Onderzoek of dit verschil bij r = 100 groter is dan bij r = 500. Licht je antwoord toe.
Iemand trekt uit bovenstaande figuur de volgende twee conclusies:
  1. In deze medische rapporten heeft een meerderheid van de gebruikte woorden een hogere frequentie dan de wet van Zipf voorspelt voor teksten met deze omvang.
  2. Deze medische rapporten bevatten minder verschillende woorden dat de wet van Zipf voorspelt voor teksten met deze omvang.
4p 11. Geeft over elk van deze conclusies een gemotiveerd oordeel.

 
In de figuur hierboven zie je dat er in de medische rapporten woorden voorkomen die dezelfde frequentie hebben. Volgens de wet van Zipf zou dit niet kunnen. Deze wet,  fr  = 88000/r , zegt dat fr steeds minder snel afneemt naarmate r toeneemt.
4p 12. Stel de afgeleide van fr op en toon met deze afgeleide aan dat voor de wet van Zipf inderdaad geldt dat fr steeds minder snel afneemt als r toeneemt.

 
Het Vierde Gewas
In de akkerbouw is het normaal dat een boer op zijn grond niet elk jaar hetzelfde gewas verbouwt. Om te voorkomen dat ziekteverwekkers in de bodem teveel invloed krijgen, is het beter in de loop van de jaren verschillende gewassen te verbouwen.

Het bedrijf Zaanstra heeft 36 ha akkerland. Op 12 ha ervan worden aardappelen geteeld, op 12 ha suikerbieten en op de overige 12 ha granen. Een jaar later wordt er op de drie stukken land gewisseld van gewas en een jaar later nog een keer. Zo wordt elk gewas eens per drie jaar op elk stuk grond verbouwd.
Per jaar kost het bewerken van één ha aardappelen aan menskracht 19 werkdagen. Voor suikerbieten is dat 20 werkdagen en voor granen 24 werkdagen.

Bij het bedrijf overweegt men nog een gewas te gaan telen en het akkerland dus te verdelen over vier gewassen, elk 9 ha. Dan krijgen ziekteverwekkers nog minder kans en dat verhoogt de kwaliteit van de oogst.
Het bedrijf stelt als voorwaarde dat het totale aantal werkdagen per jaar niet hoger mag worden. Dat betekent dat er voor zo'n vierde gewas ten hoogste 189 werkdagen per jaar beschikbaar zijn.
3p 13. Laat zien dat het getal 189 juist is.

 
Voor dit vierde gewas heeft het bedrijf de keuze uit verschillende plantensoorten, waarvan de zaden veel bruikbare oliën en vetten bevatten. In de volgende tabel staan enkele gegevens over deze plantensoorten.
  akkermoesbloem komkommmerkruid teunisbloem
werkdagen (per ha) 16 22 24
oogst in kg (per ha) 1000 800 800
opbrengst (per kg) € 3,00 € 4,00 € 4,50
Voor het bewaren van de oogst van deze gewassen beschikt het bedrijf over een koelruimte waar men ten hoogste 8400 kg zaden kan opslaan.

We kunnen de conclusie trekken dat het voor Zaanstra niet mogelijk is de 9 ha helemaal te gebruiken voor de teelt van slechts één van de drie plantensoorten akkermoesbloem, komkommerkruid of teunisbloem.
3p 14. Toon dit aan.

 
We willen nagaan welke verdeling van de beschikbare 9 ha grond over de drie plantensoorten de grootst mogelijke opbrengst oplevert. Het aantal ha dat wordt gebruikt voor akkermoesbloem geven we aan met x, dat voor komkommerkruid met y en dat voor teunisbloem dus met 9 - x - y.
Naast de voorwaarden  x ³ 0 en y ³ 0 gelden voor mogelijke oplossingen ook de voorwaarden:
I:     x + y ≤ 9
II:    x ≤ 6
III:   8x + 2y ≥ 27
5p 15. Toon aan dat de voorwaarden II en III volgen uit bovenstaande gegevens.

 
8p 16. Onderzoek bij welke verdeling van de grond over de drie plantensoorten de jaarlijkse opbrengst voor Zaanstra zo groot mogelijk is.

 
Al doende leert men
In de Amerikaanse industrie is ooit onderzocht hoe snel werknemers leren wanneer zij een handeling vaker verrichten. Bij een groot aantal werknemers is bijgehouden hoeveel tijd ze nodig hadden om een bepaalde handeling voor de eerste keer te verrichten, hoeveel tijd voor de tweede keer, enz.

Zo bleken werknemers 16 minuten nodig te hebben om handeling A voor de eerste keer te verrichten. Bij de tweede keer was die handelingstijd 12,8 minuten. Dus wanneer een werknemer handeling A twee keer heeft uitgevoerd is zijn gemiddelde handelingstijd  (16 + 12,8)/2 = 14,4 minuten. Deze 14,4 minuten zie je in de volgende tabel. De andere waarden in deze tabel zijn op een vergelijkbare manier berekend.
aantal keren dat handeling A is verricht (n) 1 2 3 4 5 6
gemiddelde handelingstijd in minuten. 16 14,4 13,1 12,1 11,3 10,7
Met behulp van deze tabel kunnen we berekenen dat een werknemer 8,1 minuten nodig heeft om handeling A voor de 5e keer te verrichten.
3p 17. Geef zo'n berekening.

 
We willen een formule opstellen voor de gemiddelde handelingstijd Hn.
Daartoe kijken we eerst naar de tijd Tn die een werknemer nodig heeft om handeling A voor de nde keer te verrichten. Tn kan goed benaderd worden met de volgende formule:
Tn = 6 + 10 • 0,68n - 1

In deze formule is Tn in minuten. Inderdaad levert deze formule T1 ≈ 16 en T2 ≈ 12,8.
Aan deze formule kun je zien dat de handelingstijd steeds korter wordt naarmate n toeneemt. Toch zal er altijd enige tijd nodig blijven om handeling A uit te voeren. dat betekent dat er op den duur vrijwel geen tijd meer wordt gewonnen.
3p 18. Hoeveel minuten is de handelingstijd op den duur korter dan de eerste handelingstijd? Licht je antwoord toe.

 
Om een formule voor Hn op te stellen merken we op dat geldt:

We moeten dus eerst de som T1 + T2 + T3 + ... + Tn van de eerste n termen berekenen.
Elk van deze termen bestaat uit een constante (het getal 6) en een exponentieel deel. De exponentiële delen vormen een meetkundige rij. Dat betekent dat we voor de som ervan gebruik kunnen maken van de somformule van een meetkundige rij.
Dat leidt tot de volgende formule voor de gemiddelde handelingstijd:
6p 19. Leid deze formule af met behulp van de formule voor Tn.

 
We noemen een werknemer ervaren voor handeling A wanneer de gemiddelde handelingstijd minder dan 7 minuten is.
In de industrie wil men graag weten hoe lang het duurt voordat een werknemer zo ver is gekomen.
3p 20. Onderzoek hoeveel handelingen een werknemer achter elkaar moet uitvoeren volgens de formule voor Hn voordat hij ervaren voor handeling A kan worden genoemd.

 
OPLOSSINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. De kans dat een auto niet gekeurd wordt is 0,97.
De kans dat geen één van vijf auto's wordt gekeurd is dan 0,975 = 0,8587
   
2. Het aantal foute keuringen moet dan 1 of 0 zijn.
binomcdf(5, 0.2 , 1) = 0,7373
of  binompdf(5, 0.2 , 0) + binompdf(5, 0.2 , 1) = 0,7373
   
3. De kans op 1,5 strafpunten is 0,1 en de kans op 0,4 bonuspunten is 0,9.
Gemiddeld geeft dat per auto  -1,5 • 0,1 + 0,4 • 0,9 = 0,21 punten.
Voor 8 auto's zal dat gemiddeld  8 • 0,21 = 1,68 punten opleveren.
   
4. Voor een schatting van de gemiddelde levensduur doen we alsof alle metingen zich bij het klassenmidden bevinden.
De klassenmiddens zijn : 2,5 en 7,5 en 12,5 en 17,5 en 22,5
De percentages zijn ongeveer (aflezen) :  3, 10, 68, 18 en 1
Het gemiddelde is dan  (2,5 • 3 + 7,5 • 10 + 12,5 • 68 + 17,5 • 18 + 22,5 • 1)/100 = 12,7

(invoeren in L1 (middens) en L2 (percentages) en dan 1-var-stats (L1,L2) kan natuurlijk ook)  
   
5. één mogelijke volgorde is eerst 2 klaveren en dan 11 anderen.
De kans daarop is  (13/52) • (12/51) • (39/50) • (38/49) • (37/48) • (36/47) • ... • (29/40) ≈ 0,00264
Er zijn 13 nCr 2  = 78 zulke volgorden
De kans wordt dan 78 • 0,00264 ≈ 0,2059

of
kies 2 klaveren uit de 13; dat kan op 13 nCr 2 = 78 manieren
kies 11 andere kaarten uit de 39. Dat kan op  39 nCr 11 = 1676056044 manieren.
samen kan dat op 78 • 1676056044   = 1,307 • 1011 manieren.
in totaal zijn er 52 nCr 13 = 6,35 • 1011 manieren om 13 willekeurige kaarten uit de 52 te kiezen.
De kans dat het 2 klaveren en 11 anderen wordt is dan  (1,307 • 1011)/( 6,35 • 1011) = 0,2059
   
6. De kans op geen klaveren is 0,013
1 van de 10 keer heeft dan kans  binompdf(10 , 0.013 , 1) = 0,1156

of:
kans op geen klaveren in 0,013, en op wel dus 1 - 0,013 = 0,987
1 van de 10 heeft dan kans  10 nCr 1 • 0,0131 • 0,9879 = 0,1156
   
7. de cumulatieve aantallen zijn  130, 932, 2992, 5857, 8242, 9487, 9901, 9988, 10000
de percentages zijn dan ongeveer:  1,3  -  9,3  -  29,9  - 58,6  -  82,4 - 94,9 - 99,0 - 99,9 - 100
daarbij horen de x-waarden  0,5 - 1,5 - 2,5 - 3,5 - 4,5 - 5,5 - 6,5 - 7,5 - 8,5
teken deze punten op normaal-waarschijnlijkheidspapier, dan geeft dat (ongeveer) een rechte lijn.
daarom zijn deze metingen ongeveer normaal verdeeld.
Douwes vermoeden is dus juist. 
   
8. H0:  μ = 325,  σ = 1,365
Maar voor 100 spellen wordt dat  H0:  μ = 325,  σ = 1,365 • √100 = 13,65
H1 : μ < 325, dus de toets is éénzijdig.
De meting is 302.5
De overschrijdingskans is  normalcdf(0, 302.5, 325, 13.65) = 0,0496
Dat is kleiner dan 0,05 dus H0 moet worden verworpen: er is inderdaad voldoende aanleiding om te veronderstellen dat 'Split' Bert te weinig klaverenkaarten geeft.
   
9. 2,3• C • logC = 495378
Deze is niet algebraïsch op te lossen. Dus Y1 = 2,3 • X • logX en Y2 = 495378
Dan intersect levert (met bijv. window Xmin = 0, Xmax = 100000, Ymin = 0, Ymax = 1000000):
X = C = 46175,539  en dat is afgerond op duizendtallen 46000
   
10. Bij r = 100 is het verschil ongeveer 1800 - 800 = 1000
Bij r = 500 is het verschil ongeveer 350 - 150 = 200
Dus het verschil bij r = 100 is groter dan bij r  = 500
   
11. Het gedeelte van de grafiek boven de rechte lijn heeft een grotere frequentie dan Zipf voorspelt.
Dat zijn de rangnummers 2 tot (ongeveer) 2200, dus dat zijn ongeveer 2200 woorden en dat is minder dan de de helft van het totaal (20000 woorden) dus stelling 1 is onwaar

De Zipf-lijn loopt verder naar rechts door dan de werkelijke lijn, dus Zipf omschrijft situaties met meer woorden, dus stelling 2 is waar.
   
12. fr = 88000 • r -1
f 'r = -88000 • r -2
deze laatste uitdrukking is altijd negatief, dus is de grafiek van fr altijd dalend.
maar f 'r gaat steeds dichter naar nul toe, dus de helling van fr ook, dus wordt fr steeds minder dalend.
   
13. In totaal zijn er 19 • 12 + 20 • 12 + 24 • 12 = 756 werkdagen in een jaar.
Voor  aardappelen, suikerbieten en granen zijn al 9 • 19 + 9 • 20 + 9 • 24 = 567 dagen nodig
Dus zijn nog 756 - 567 = 189 dagen over voor de nieuwe gewassen.
   
14. akkermoesbloem heeft een totale oogst van 9 • 1000 = 9000 kg en dat is teveel (meer dan 8400)
komkommmerkruid vergt 9 • 22 = 198 werkdagen en dat is teveel (meer dan 189)
teunisbloem vergt 9 • 24 = 216 werkdagen en dat is teveel (meer dan 189)
   
15. de totale oogst wordt  x • 1000 + y • 800 + (9 - x - y) • 800 = 1000x + 800y + 7200 - 800x - 800y
dat is 200x + 7200 en dat moet minder zijn dan de opslagcapaciteit 8400
200x + 7200 ≤ 8400  ⇒  200x ≤ 1200  ⇒  (delen door 200) ⇒ x ≤ 6

Het totale aantal werkdagen wordt  16 • x + 22 • y + 24 • (9 - x - y) = 16x + 22y + 216 - 24x - 24y
dat is -8x - 2y + 216 en dat moet minder zijn dan 189
-8x - 2y + 216 ≤ 189 ⇒ -8x - 2y ≤ -27  ⇒ 8x + 2y ≥ 27
   
16. Teken de vijf grenslijnen die boven opgave 15 staan in een toelaatbaar gebied:

Hoekpunten:  A = (3.375 , 0)  B = (6,0)  C = 6,3)
D:  x + y = 9  ⇒  2x + 2y = 18
trek deze vergelijking af van 8x + 2y = 27; dat geeft  6x = 9  ⇒  x  = 1,5  en  D = (1.5 , 7.5)
 
De opbrengst is 3 • 1000 • x + 4 • 800 • y + 4,5 • 800 • (9 - x - y) = 3000x + 3200y + 32400 - 3600x - 3600y
Dat is 32400 - 600x - 400y

Invullen in de vier punten A,B,C en D geeft achtereenvolgens  30375 , 28800 , 27600 en 28500
De opbrengst is maximaal in punt A, dus bij de verdeling:  3,375 ha akkermoesbloem en 0 ha komkommerkruid en 5,625 ha teunisbloem.
   
17. Vijf  keer handeling A kost in totaal  5 • 11,3 = 56,5 minuten
Vier keer handeling A kost in totaal  4 • 12,2 = 48,4 minuten.
Dus kostte de vijfde keer  56,5 - 48,4 = 8,1 minuten.
   
18. Als n oneindig groot wordt, dan wordt Tn gelijk aan 6.
De eerste handelingstijd was 16 minuten, dus de winst is 10 minuten.
   
19. n keer het constante getal 6 levert in totaal 6n

de meetkundige rij heeft begingetal 10 en reden 0,68.

dat geeft voor de som

De totale som wordt dan  6n + 31,25 • (1 - 0,68)n
Voor het gemiddelde moeten we dit door n delen, en dat geeft precies de gevraagde formule.
   
20. H = 7 moet opgelost worden.
voer in Y1 = H  en  Y2 = 7 en gebruik calc - intersect om het snijpunt te vinden
Dat geeft X = 32