VWO WA1,2    2001 - I
Contradansen
Een Engelse contradans is een muziekstuk dat uit twee delen bestaat. Ieder deel bestaat uit acht maten. In het boekje "Musik mit Würfeln" staat een systeem beschreven om, zonder enige muzikale kennis, zelf zulke contradansen te maken met behulp van twee dobbelstenen. In dit boekje staan 176 verschillende maten uitgeschreven. Deze maten zijn genummerd van 1 tot en met 176.

De getallen 1 tot en met 176 zijn verdeeld over twee even grote tabellen. De tabel die nodig is voor het eerste deel van de contradans is hieronder afgebeeld.

 

de eerste acht maten
aantal ogen:   A B C D E F G H
2 70 14 164 122 25 153 18 167
3 10 64 100 12 149 30 161 11
4 33 1 160 163 77 156 168 172
5 36 114 8 35 111 39 137 44
6 105 150 57 71 117 52 132 130
7 165 152 112 15 147 27 73 102
8 7 81 131 37 21 125 49 115
9 142 106 40 69 43 140 23 89
10 99 68 86 139 120 92 143 83
11 85 45 90 158 82 123 78 58

12

 145 97 6 121 56 67 63 16


De andere tabel, die nodig is voor het tweede deel van de contradans, zullen we hier niet gebruiken.
Door nu acht keer met twee zuivere dobbelstenen te gooien kun je in de tabel aflezen uit welke maten het eerste deel van de contradans zal bestaan. Gooi je bijvoorbeeld bij de eerste worp samen 10 ogen dan lees je in kolom A af dat maat 99 de eerste maat is. Gooi je daarna bijvoorbeeld samen 5 ogen dan lees je in kolom B af dat maat 114 de tweede maat is. Zo ga je door totdat je uit elk van de kolommen A tot en met H één maat hebt gekozen. de aldus verkregen acht maten vormen het eerste deel van de contradans.
Iemand beweert dat er op deze wijze meer dan 200 miljoen verschillende eerste delen van contradansen gemaakt kunnen worden.
3p 1. Onderzoek of deze bewering waar is.

 
Het is mogelijk dat na drie keer gooien met de beide dobbelstenen de maten 36 - 114 - 8 de eerste drie maten vormen van het eerste deel van de contradans.
4p 2. Bereken de kans op deze volgorde.

 
Iemand beweert dat de kans dat maat H een nummer heeft dat groter is dan 100 gelijk is aan 5/11. Immers, in de kolom onder H staan 11 getallen waarvan er 5 groter zijn dan 100.
Met een berekening kunnen we aantonen dat deze bewering niet waar is.
6p 3. Bereken hoe groot deze kans wél is.

 
Wijnvoorraad
Een wijnboer heeft op 1 januari 2001 een wijngaard gekocht die goed is voor een jaarproductie van 400 hL wijn (1 hL = 1 hectoliter = 100 liter).
De wijnboer wil kwaliteitswijn produceren die lang houdbaar is. Na de oogst wordt de nieuwe wijn twee jaar lang in eikenhouten vaten bewaard om te rijpen. Na die twee jaar wordt de wijn gebotteld (in flessen gedaan). In de flessen rijpt de wijn nog verder waardoor de verkoopwaarde van de wijn toeneemt.
Als de wijnboer elk jaar direct al zijn gebottelde wijn verkoopt dan kan hij niet van deze waardevermeerdering profiteren Maar als hij al zijn  gebottelde wijn opslaat in zijn wijnkelders dan raken deze snel vol en heeft de wijnboer voorlopig geen inkomsten.
De wijnboer besluit om jaarlijks een vast percentage van zijn totale voorraad gebottelde wijn te verkopen. Hij verkoopt de wijn altijd aan het eind van het jaar nadat de gebottelde wijn aan de voorraad is toegevoegd.

Als de wijnboer er bijvoorbeeld voor kiest om elk jaar 25% van zijn totale voorraad gebottelde wijn te verkopen dan ontwikkelt de voorraad zich de eerste jaren als in de tabel hieronder.

  1 januari
2001		 1 januari
2002		 1 januari
2003		 1 januari
2004		 1 januari
2005		 1 januari
2006
nieuwe wijn (hL) 0 400 400 400 400 400
eenjarige wijn (hL) 0 0 400 400 400 400
gebottelde wijn (hL) 0 0 0 300 525 693,75
3p 4. Bereken de totale hoeveelheid gebottelde wijn op 1 januari 2007 als de wijnboer jaarlijks 25% van al zijn flessen wijn verkoopt. Geef je antwoord in liters nauwkeurig.

 
Ook voor de rest van deze opgave bekijken we de voorraad van de wijnboer alleen maar op 1 januari van ieder jaar.
Bij een ander percentage ontwikkelt de totale voorraad van de wijnboer zich natuurlijk anders. Het vaste percentage van de gebottelde wijn dat de wijnboer jaarlijks verkoopt noemen we p. De tijd in jaren noemen we t. Hierbij nemen we t = 0 op 1 januari 2001. De totale voorraad gebottelde wijn (in hL) op tijdstip t noemen we Gt.
Gedurende de eerste paar jaren is G gelijk aan 0:  G0 = 0, G1 = 0  en G2 = 0
En verder geldt de volgende formule:

De totale voorraad gebottelde wijn groeit in de loop van de tijd naar een evenwichtswaarde. Deze evenwichtswaarde hangt af van de gekozen waarde van p.
Voor het verband tussen p en de evenwichtswaarde (in hL) geldt de volgende formule:

evenwichtswaarde = 40000/p  -  400

Deze formule voor de evenwichtswaarde is uit bovenstaande formule voor Gt af te leiden.
5p 5. Leid bovenstaande formule voor de evenwichtswaarde af.

 
In de wijnkelders van de wijnboer kunnen slechts 280000 flessen wijn worden opgeslagen. In een fles zit 0,75 liter wijn.
5p 6. Bereken bij welke waarden van p de wijnkelders op den duur niet voldoende capaciteit hebben

 
De wijnboer besluit om jaarlijks 10% van zijn totale voorraad gebottelde wijn te verkopen.
Door een verbouwing kan hij nu 2400 hL gebottelde wijn in zijn kelders opslaan.
6p 7. Onderzoek met behulp van de hierboven vermelde formule voor Gt en het gegeven dat G2 = 0 in welk jaar de capaciteit van de wijnkelders voor het eerst niet meer voldoende is.

 
Kwaliteitscontrole
In een fabriek worden plastic zakken gevuld met suiker. De vulmachine staat afgesteld op 510 gram.
Neem aan dat het gewicht van de zakken suiker normaal verdeeld is met een gemiddelde m  van  510 gram en een standaardafwijking s van 4 gram.
3p 8. Bereken hoeveel procent van alle zakken een gewicht minder dan 500 gram zal hebben.

 
Om de kwaliteit van het vulproces te bewaken wordt elk uur een aselecte steekproef van 5 zakken suiker genomen. Van elke zak noteert men het gewicht. Ook wordt van de steekproef het totale gewicht T berekend.
5p 9. Bereken de kans dat het totale gewicht van de steekproef minder is dan 2525 gram.

 
Verder bepaalt men van elke steekproef het gemiddelde gewicht x en de spreidingsbreedte R (dat is het verschil tussen de grootste en de kleinste meting).
Men noteert al deze gegevens op een controlekaart, de x/R-kaart. Op de x/R-kaart hieronder staan de meetresultaten van 10 steekproeven.
Iedere steekproef bestaat uit 5 zakken. Op de controlekaart worden de afwijkingen van 500 gram bij ieder van deze zakken genoteerd als  x1, x2, x3, x4 en x5.
Zo heeft de derde zak van de tweede steekproef een gewicht van 509 gram. Dit is genoteerd als 9.
Het gemiddelde van de eerste steekproef is 509,6 gram. Dit wordt dan genoteerd als 9,6.
De spreidingsbreedte van de eerste steekproef is 515 - 504 = 11 gram.
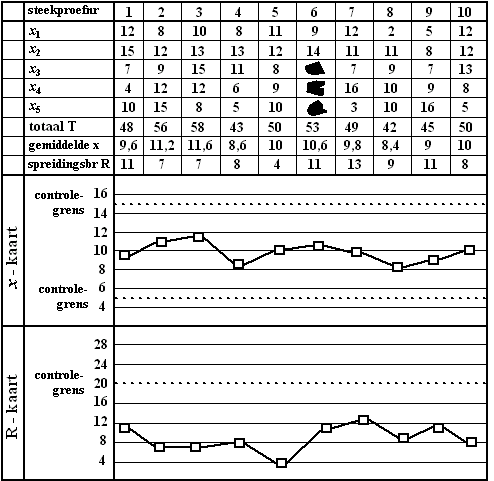Bij steekproef nr. 6 zijn enkele gegevens onleesbaar geworden.
3p 10. Welke getallen kunnen hier bijvoorbeeld gestaan hebben? Licht je antwoord toe.

 
Bij de controle van het vulproces met behulp van de xR-kaart let men erop of x of R de zogeheten controlegrenzen overschrijden. Deze controlegrenzen zijn in de grafieken met stippellijnen aangegeven. Zodra bij een steekproef een van deze grenzen overschreden wordt slaat men alarm.
Op een gegeven moment slaat men alarm bij een steekproef terwijl met de waarde van x niets mis is.
4p 11. Wat zouden de vijf gewichten in deze steekproef bijvoorbeeld kunnen zijn? Licht je antwoord toe.

 
De zakken zijn bedrukt met het bedrijfslogo. Soms is dit logo onscherp afgedrukt. Volgens de afdeling Verpakkingen heeft 5% van de zakken een onscherp logo. Een werknemer van die afdeling vermoedt echter dat dit percentage hoger is dan 5%. Er wordt een steekproef getrokken van 50 zakken. Op 6 van de 50 zakken is het bedrijfslogo onscherp.
5p 12. Onderzoek of de 6 zakken met het onscherpe bedrijfslogo voldoende aanleiding zijn om de werknemer in het ongelijk te stellen. Neem als significantieniveau  α = 0,025

 
Koeling
Wageningse onderzoekers hebben zich verdiept in de groei van het aantal bacteriën in voedsel. Bij constante bewaartemperatuur groeit het aantal bacteriën exponentieel. De bijbehorende groeifactor hangt af van de bewaartemperatuur.
In een krantenartikel hierover stond de grafiek hieronder. De schaalverdelingen langs de assen zijn zo gekozen dat de grafieken, die de groei van het aantal bacteriën weergeven, rechte lijnen zijn.
In de grafiek wordt de bacteriegroei beschreven in kip die bij 0 °C (winkel A) respectievelijk 4 °C (winkel B) wordt bewaard.
4p 13. Toon aan dat bij 0 °C het aantal bacteriën zich per dag meer dan verdubbelt.

 
In de grafiek is het aantal bacteriën per gram bij het begin gelijk aan 1000. De bederfgrens ligt bij 50 miljoen bacteriën per gram. In de figuur is af te lezen dat kip, die voortdurend op 0 °C wordt bewaard, na 14 dagen de bederfgrens bereikt.

Door verbeterde hygiëne is men in staat het aantal bacteriën bij het begin terug te brengen van 1000 per gram naar 100 per gram. Dit verlengt de houdbaarheid natuurlijk.c Bij bewaren b ij 0 °C (winkel A) duurt het dan in totaal 17 dagen voordat de bederfgrens bereikt wordt. De houdbaarheid wordt dus met 3 dagen verlengd.
Bij bewaren bij 4 °C (winkel B) wordt de houdbaarheid door die verbeterde hygiëne met minder dan 3 dagen verlengd. De groeifactor per dag die bij 4 °C hoort is 8,3.
5p 14. Met hoeveel dagen wordt de houdbaarheid bij 4 °C door die verbeterde hygiëne verlengd? Licht je antwoord toe. Je kunt daarbij gebruik maken van de figuur hierboven.

 
Om de grafiek hierboven te tekenen gebruikten de onderzoekers een formule voor het verband tussen de bewaartemperatuur T en de groeifactor per dag g van het aantal bacteriën.
Bij het opstellen van deze formule waren zij er van uit gegaan dat bacteriegroei alleen optreedt boven een bepaalde minimumtemperatuur. Deze minimumtemperatuur T0 hangt af van het soort voedsel. Voor elk soort voedsel heeft de formule de volgende vorm:

g = 10(c(T - T0))²

In deze formule is T in ºC met T ≥ T0 en is c een constante.
We kunnen controleren dat er volgens deze formule inderdaad geen bacteriegroei optreedt als T = T0
3p 15. Voer deze controle uit.

 
Uit praktische overwegingen schrijft men de formule voor de groeifactor vaak in de vorm  g = 10m. Deze variabele m is afhankelijk van T. Er geldt:  √m = c • (T - T0)
Voor elk soort voedsel moeten c en T0 experimenteel bepaald worden. Zo heeft men voor kip bij allerlei bewaartemperaturen de bacteriegroei gemeten.
Bij de verwerking van de metingen hebben de onderzoekers het verband tussen T en √m in een grafiek gezet, omdat dit verband volgens de formule lineair is. Het resultaat staat hieronder.
6p 16. Leid uit de grafiek van dit lineaire verband benaderingen af voor de constanten c en T0. Je kunt bij de beantwoording gebruikmaken van de figuur hierboven.

 
Ga er in de rest van deze opgave van uit dat geldt:  c = 0,096 en T0 = - 6

In de grafiek helemaal bovenaan deze opgave kunnen we aflezen dat kip met een aantal bacteriën van 1000 per gram bij het begin na 14 dagen de bederfgrens bereikt wanneer die wordt bewaard bij een temperatuur van 0 ºC

Het kan echter ook voorkomen dat deze kip tijdens het transport een halve dag (12 uur) wordt bewaard bij een temperatuur van 18 ºC en daarna steeds bij 0 ºC.
5p 17. Hoeveel eerder wordt dan de bederfgrens bereikt? Licht je antwoord toe en gebruik eventueel de grafiek helemaal bovenaan deze opgave.

 
Kosten bij plastics
Bij industriële productieprocessen worden de totale productiekosten voornamelijk bepaald door de grootte van de installaties die daarvoor gebruikt worden. Dit is bijvoorbeeld het geval bij de productie van plastics.
In deze opgave bekijken we zo'n productieproces. Alle bedragen in deze opgave zijn op jaarbasis. Voor een bedrijf waar een dergelijk productieproces plaatsvindt gebruikt men de volgende formule voor de kosten K:

K = 25000 • P0,62

In deze formule is K in dollars en is P de productie in tonnen per jaar.
De grafiek die bij deze formule hoort zie je in onderstaande figuur.
In de grafiek zien we dat de kosten toenemen als de productie toeneemt. Het is de vraag of ook de marginale kosten K'  toenemen bij toenemende productie.
5p 18. Onderzoek of de marginale kosten toenemen bij toenemende productie.

 
Ook de opbrengst hangt af van de productie. Men gebruikt hiervoor de formule:

O = 750•P

In deze formule is de opbrengst O in dollars en is P weer de productie in tonnen per jaar.

We willen nu onderzoeken op welke wijze de productie van plastics het best kan worden ingericht; de vraag is dan of de producent moet kiezen voor grootschalige dan wel kleinschalige productie. Doelstelling hierbij is dat de producent zo veel mogelijk winst wil maken.

Iemand gaat er van uit dat de maximale winst gevonden wordt als de marginale kosten K' gelijk zijn aan de marginale opbrengst O'. Hij berekent daartoe voor welke waarde van P geldt dat K' = O'.
5p 19. Bereken deze waarde van P.
De in vraag 19 berekende waarde van P levert echter niet de maximale winst op.
5p 20. Leg uit of de producent zijn productie grootschalig of kleinschalig moet inrichten om zoveel mogelijk winst te maken.

 
OPLOSSINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. Per worp zijn er 11 verschillende mogelijke uitkomsten (nl.  2 tm 12)
Over 8 worpen zijn er dus  118 = 214.358.881 verschillende uitkomsten mogelijk.
Dat is meer dan 200 miljoen dus de bewering is juist.
2. Om te beginnen met de maten 36 - 114 - 8 moet driemaal 5 gegooid worden.
Van de 36 verschillende mogelijk worpen leveren er vier een uitkomst 5   (nl. (1,4)(2,3)(3,2)(en (4,1))
De kans op 5 bij 1 keer gooien is dus  4/36.
Drie keer achter elkaar 5 geeft een kans  (4/36)3 = 0,0014
3. De nummers boven de 100 horen bij de worpen met uitkomst 2,4,6,7 en 8.
P(2) = 1/36   (1,1)
P(4) = 3/36   (1,3)(2,2)(3,1)
P(6) = 5/36   (1,5)(2,4)(3,3)(4,2)(5,1)
P(7) = 6/36   (1,6)(2,5)(3,4)(4,3)(5,2)(6,1)
P(8) = 5/36   (2,6)(3,4)(4,4)(5,3)(6,2)
Samen is dat een kans van 20/26 = 0,56
4. Op 1 januari 2006 is er 693,75 hL gebottelde wijn.
In de loop van dat jaar wordt er nog 400 hL gebottelde wijn aan toegevoegd.
Van de gebottelde voorraad wordt 25% verkocht, dus er blijft nog 75% over.
0,75 • (693,75 + 400) = 820,3125 hL ≈ 82031 liter
5. Bij evenwicht geldt  Gt = Gt-1. Noem deze evenwichtswaarde G, dan geldt:
G = (1 - p/100)•G + 400 - 4p  ⇒  G = G - G• p/100 + 400 - 4p  ⇒  G • p/100 = 400 - 4p
⇒  G • p = 40000 - 400p ⇒ G = (40000 - 400p)/p  =  40000/p  - 400  en dat is de gevraagde formule.
6. 280000 flessen van 0,75 liter bevatten in totaal 210000 liter = 2100 hL.
Het gaat erom dat de evenwichtswaarde G hier niet boven ligt.
1e opl. Y1 = 40000/x - 400  en Y2 = 2100 invoeren in de GR
INTERSECT geeft x = 16.
Dus als p < 16 dan zullen de kelders uiteindelijk onvoldoende capaciteit hebben.
2e opl. 40000/x - 400 = 2100 ⇒  40000/x = 2500 ⇒ x = 40000/2500 = 16 
met dezelfde conclusie als in de eerste oplossing.
7. Bij 10% verkopen is p = 0,10
Dat geeft  Gt = (1 - 10/100) • Gt-1 + 400 - 4 • 10  =  0,9•Gt-1 + 360
GR:  MODE SEQ, en dan bij Y= invoeren
nmin = 2
u(n) = 0,9 • u(n - 1) + 360
u(nmin) = 0
TABLE levert dan  n = 12,  u(n) = 2344,75...  en  n = 13,  u(n) = 2470,28...
Dus op t = 13, dat wil zeggen op 1 januari 2014, is de hoeveelheid boven de 2400 hL.
8. NORMALCDF(-1E99 , 500, 510, 4) = 0,0062 dus het betreft 0,62% van de zakken.
9. Voor de som T van vijf zakken geldt:
 μT = 5 • 510 = 2550
 σT2 = σ12 + σ22+ ... + σ52 = 16 + 16 + ... + 16 = 5 • 16 = 80  dus σT = √80 
(dat kan ook direct met de √n -wet trouwens)
NORMALCDF(-1E99 , 2525 , 2550 , √80) = 0,0026
10. Het totaal van de vijf waarnemingen is 53.  x1 + x2 = 23 dus de gezochte drie zijn samen 30.
Het verschil tussen de grootste en kleinste van de vijf moet 11 zijn.
Er zijn meerdere goede oplossingen, bijv: 14 , 13 , 3  of  16 , 9 , 5
11. We zoeken vijf getallen waarvan de spreiding groter is dan 20, maar waarvan het gemiddelde wel tussen de 5 en 15 ligt. Er zijn vele goede oplossingen.
Bijv. 0,0,0,0,30  met bijbehorende gewichten  500, 500, 500, 500, 530.
12. H0:  p = 0,05
H1:  p > 0,05  dus éénzijdig.
X is het aantal zakken met onscherp logo. Dan is X binomiaal verdeeld met n = 50, en p = 0,05 (volgens H0)
De meting is 6 zakken.
Dat heeft een overschrijdingskans van P(X ≥ 6) = 1 - P(X ≤ 5) = 1 - BINOMCDF(500 , 0.05 , 5) = 1 - 0,9622 = 0,0378
Dat is groter dan 0,025 dus H0 kan niet verworpen worden: er is onvoldoende aanleiding om de werknemer in het gelijk  te stellen.
13. 1e opl. In de grafiek kun je aflezen dat er op t = 0:  103 = 1000 bacteriën zijn en op t = 3: 104 = 10000.
De groeifactor per 3 dagen is dus 10, dus per dag  101/3 = 2,15. Dat is groter dan 2.
2e opl. Als de groeifactor 2 zou zijn, dan zouden er na bijv. 3 dagen 103 • 2 • 2 • 2 =   8000 bacteriën zijn.
Maar er zijn na 3 dagen al 10000 bacteriën. Dus moet de groeifactor wel groter dan 2 zijn.
14. 1e opl. De nieuwe grafiek begint bij (0,100) en loopt evenwijdig aan de oude voor winkel B.
De nieuwe grafiek snijdt de bederfgrens dan ongeveer bij  t = 6,2.
Dat was bij de oude grafiek t = 5, dus de houdbaarheid wordt 1,2 dag verlengd.
2e opl. Voor de nieuwe situatie geldt:  A = 100 • 8,3t (waarin A het aantal bacteriën is)
100 • 8,3t = 50000000  ⇒  8,3t = 500000  ⇒  t = log(500000)/log(8,3) = 6,2
Dat is 1,2 dagen langer dan in de oude situatie.
(de vergelijking 100 • 8,3t = 50000000  kan natuurlijk ook opgelost worden door beide leden in te voeren in de GR bij Y1 en Y2, en het snijpunt t = 6,2 met INTERSECT te vinden)
15. T = T0 invullen in de gegeven formule:

De groeifactor is 1, dus de hoeveelheid bacteriën blijft gelijk.
16. √m = c • (T - T0)  ⇒  √m = c • T - c • T0
Dit is een lineair verband tussen T en √m waarbij c het hellinggetal is en  -c • T0 het begingetal.
Uit de grafiek is af te lezen:  T = 2 dan is   √m = 0,75  en verder  T = 20 dan is  √m = 2,5
Het hellinggetal van de lijn is dus  Δy/Δx = (2,5 - 0,75)/(20 -  2) = 0,097  dus  c = 0,097
(2, 0.75) invullen geeft  0,75 = 0,097 • 2 + 0,097 • T0  dus  T0 = 5,73
17. T = 18 , c = 0,096 en T0 = -6 geeft  g = 10(0,096•(18--6))²= 203430
Na 12 uur is het aantal dus gestegen tot  1000 • 2034300,5 = 451032
Daarna groeit het door met de groeifactor 2,15 per dag.
Op te lossen:  451032 • 2,15t = 50000000 dus 2,15t = 50000000/451032 = 110,856... 
dus  t = log(110,856...)/log(2,15) = 6,1508...
De bederfgrens wordt dus bereikt na  0,5 + 6,15 = 6,7 dagen, en dat is 7,3 dagen eerder dan wanneer de kip bij 0º zou zijn bewaard.
18. De marginale kosten zijn gelijk aan de helling van de grafiek.
Aan de figuur is duidelijk te zien dat de helling afneemt (de grafiek loop "bol"), dus nemen de marginale kosten af.
19. K' = 25000 • 0,62  • P-0,38 = 15500 • P-0,38   en O'  = 750
K ' = O ' geeft dus  15500 • P-0,38 = 750 ⇒  P - 0,38 = 750 / 15500 = 0,0483..  
⇒  P = 0,0483...(1/-0,38) = 2892  
20. Winst = Opbrengst - Kosten   ⇒  W = 750P - 25000•P0,62
Een Plot van W ziet er zo uit: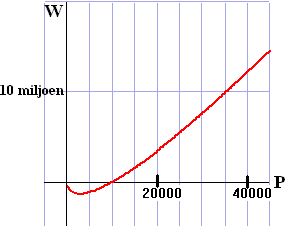



Bij lage productie is er verlies, bij stijgende productie neemt de winst steeds meer toe.
De producent kan zijn productie dus het best grootschalig inrichten.