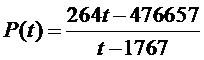VWO WA1, 2009 - II
 

 

Zeemonsters.
     
In 1972 werd de mesoplodon densirostris ontdekt in de oceaan. Het is een dolfijnensoort die 7 meter lang kan worden. Mede naar aanleiding van deze vondst deed de bioloog C. Paxton onderzoek naar de vraag hoeveel van dergelijke grote diersoorten er in de toekomst nog meer ontdekt zullen worden. Paxton beperkte zich tot wat hij zeemonsters noemde: dieren die in zee leven en meer dan 2 meter lang kunnen worden.
     

een mesoplodon densirostris
     
Op basis van gegevens over het aantal ontdekte zeemonsters in verschillende jaren stelde Paxton het volgende model op:
     

     
Met dit model kon hij een schatting maken van het aantal ontdekte soorten tot en met een zeker jaar t. In deze formule is P(t) het aantal soorten dat tot en met jaar t bekend is. Dus als je een schatting wilt van het aantal soorten dat bijvoorbeeld op het eind van het jaar 1980 bekend is, dan moet je t = 1980 invullen in de formule. De uitkomst wordt afgerond op gehelen.

Vanaf eind 1895 tot en met eind 1995 zijn er in werkelijkheid 30 soorten ontdekt.
     
3p. 1. Bereken hoeveel soorten er volgens het model van Paxton zouden zijn ontdekt in deze periode.
   

  
J. Groot schreef in 2003 een artikel in het wiskundeblad Pythagoras over het model van Paxton. Daarin schreef hij dat hij met dezelfde gegevens een ander model had gevonden. Zijn model zag er als volgt uit:
G(t) = 218 • (1−0,9799t − 1798 )
In deze formule is G(t) het aantal soorten dat tot en met jaar t bekend is. Ook hier wordt de uitkomst afgerond op gehelen.

De twee formules hierboven zijn verschillend, dus je mag verwachten dat beide modellen niet altijd dezelfde uitkomsten opleveren. Voor t = 1931 bijvoorbeeld geeft het model van Paxton 202 soorten en het model van Groot 203. Vanwege de afronding op gehelen is er een aantal jaren waarvoor de twee modellen wél dezelfde uitkomst geven. Onder andere is dat het geval bij t = 1938: beide modellen leveren dan elk 205 bekende soorten. Er zijn nog meer jaren uit de periode 1930 tot en met 1945 waarvoor beide modellen dezelfde uitkomst geven.
     
4p. 2. Onderzoek welke jaren dat zijn.
   

  
Paxton en Groot ontwikkelden hun modellen vooral om een schatting te kunnen maken van het aantal soorten zeemonsters dat men in de toekomst nog zou kunnen ontdekken. Elk van deze beide modellen voorspelt dan ook dat het aantal soorten zeemonsters een grenswaarde heeft. Volgens het model van Paxton zullen er na 2009 nog 42 soorten zeemonsters ontdekt worden.
     
4p. 3. Bereken hoeveel soorten zeemonsters er na 2009 nog ontdekt zullen worden volgens het model van Groot.
   

  
Behalve de formules van Paxton en Groot zijn er nog meer formules denkbaar die de werkelijke aantallen bekende soorten zeemonsters goed benaderen.
Een mogelijkheid is bijvoorbeeld een formule van de vorm F(t) = √(at + b) . In deze formule is F(t) het aantal soorten tot en met jaar t. De waarden voor a en b worden zo gekozen dat het model precies overeenkomt met de werkelijke aantallen soorten zoals die eind 1895 en eind 1995 bekend waren. Eind 1895 waren er in werkelijkheid 187 soorten zeemonsters bekend. Eind 1995 waren dat er 217. Er kan nu worden berekend dat de waarde van a gelijk is aan 121,2.
     
4p. 4. Bereken de waarde van b.
   

  
Conditietest.
     
Om de conditie te meten van mensen worden vaak conditietests gebruikt. De conditietest die in deze opgave vermeld wordt, is een gangbare conditietest waarbij iedere prestatie een score oplevert. Hoe hoger de score, hoe beter de conditie. In Canada is een onderzoek gedaan onder een groot aantal jongens van 12 tot en met 17 jaar. In de volgende tabel staan de resultaten van het onderzoek voor jongens van 17 jaar.
     
score 5,44 6,89 7,50 8,36 8,81 9,30 9,84 10,23 11,09 11,87 12,58
cumulatief
percentage		 5 10 20 30 40 50 60 70 80 90 95
     
In de tabel is bijvoorbeeld af te lezen dat 90% van de jongens een score van 11,87 of minder behaalt. De scores in de tabel zijn gerangschikt op cumulatief percentage. De scores van de Canadese jongens van 17 jaar zijn bij benadering normaal verdeeld. Dat kun je zien als je de scores van de tabel uitzet op normaal waarschijnlijkheidspapier.
     
3p. 5. Zet de scores van de tabel uit op het normaal waarschijnlijkheidspapier (hier kun je een velletje vinden) en leg met behulp van deze tekening uit waarom er bij benadering sprake is van een normale verdeling.
     
4p. 6. Bepaal met het normaal waarschijnlijkheidspapier van de uitwerkbijlage of met de tabel het gemiddelde en de standaardafwijking van de scores van jongens van 17 jaar.
   

  
Ook voor Canadese jongens in andere leeftijdsgroepen zijn de scores (bij benadering) normaal verdeeld.

Voor Canadese jongens van 13 jaar is het gemiddelde 7,4 en de standaardafwijking 2,0. Wanneer een jongen van 13 jaar hoger dan 9,94 scoort is er sprake van een hoge score. Uit de onderzochte groep worden willekeurig twee jongens van 13 jaar gekozen.
     
4p. 7. Bereken de kans dat ze allebei een hoge score hebben.
   

  
Voor Canadese jongens van 14 jaar is het gemiddelde 8,0 en de standaardafwijking 2,0.
We kiezen aselect 100 Canadese jongens van 14 jaar.
     
4p. 8. Bereken de kans dat hun gemiddelde score minder dan 0,1 afwijkt van 8,0.
   

  
Voor Canadese jongens van 12 jaar is de gemiddelde score 7,3. Verder is uit het onderzoek gebleken dat 77% van de jongens van 12 jaar een score had die lager was dan 8,85.
     
4p. 9. Bereken de standaardafwijking van de scores van de Canadese jongens van 12 jaar.
   

  
     
Melkvee.
     
De afgelopen jaren is het aantal melkveehouderijen afgenomen. Het (gemiddelde) aantal koeien per melkveehouderij is echter toegenomen. Beide ontwikkelingen zijn weergegeven in onderstaande figuur. Deze figuur is gebaseerd op gegevens van het Centraal Bureau voor de Statistiek (CBS).
     

     
Op basis van de gegevens in deze figuur kan worden onderzocht of het totale aantal koeien in Nederland in 2003 groter of kleiner was dan in 1975.
     
4p. 10. Voer dat onderzoek uit aan de hand van een berekening.
   

  
In de figuur is te zien dat de grafiek van het aantal koeien per melkveehouderij in de periode 2000 – 2003 minder steil loopt dan in de periode 1985 – 2000. Toch is de gemiddelde jaarlijkse toename van het aantal koeien per melkveehouderij groter in de periode 2000 – 2003 dan in de periode 1985 – 2000.
     
3p. 11. Laat dit met een berekening zien en leg uit waarom dit niet in tegenspraak is met de gegevens in de grafiek van het aantal koeien per melkveehouderij.
   

  
Koeien worden tegenwoordig gemolken door een zogenaamde melkrobot. De melkrobot melkt de koe zonder dat de boer daarbij aanwezig hoeft te zijn. In 2005 werd door de dierenbescherming het volgende persbericht gepubliceerd:
     

persbericht.

“In 2002 bleef 10% van de melkveestapel in de stal. De melkrobot heeft tot gevolg dat er steeds minder koeien in de wei komen. De dierenbescherming is daarom tegenstander van melkrobots. Dit jaar (2005 dus) blijft maar liefst 17% van de melkveestapel het hele jaar in de stal. Daardoor blijven de weilanden leeg. Als deze trend zich doorzet, verwachten wij dat over zo’n tien jaar de helft van de melkveestapel uit het Nederlandse landschap is verdwenen.”
     
Uit het persbericht blijkt dat 90% van het melkvee in 2002 in de wei komt. Ook zien we dat in 2005 nog slechts 83% van het melkvee in de wei komt. In het persbericht is sprake van een ‘trend’, maar het wordt niet duidelijk van welk model men daarbij is uitgegaan en waar “de helft van de melkveestapel” vandaan komt. Enkele voor de hand liggende modellen zijn:
  1. een trend waarbij het percentage melkvee dat in de wei komt lineair daalt;
  2. een trend waarbij het percentage melkvee dat in de wei komt exponentieel afneemt.
     
4p. 12. Bereken hoeveel procent van het melkvee in 2015 volgens model 1 en hoeveel procent volgens model 2 in de wei komt.
   

  
Voor het beschrijven van de situatie op de lange duur is model 1 op grond van wiskundige overwegingen niet bruikbaar maar model 2 misschien wel.
     
2p. 13. Leg uit waarom model 1 op de lange duur zeker niet realistisch kan zijn, maar model 2 misschien wel.
   

  
Boer Poelen vraagt zich af of het voordelig is een melkrobot aan te schaffen. De verkoopprijs van de melk is op dat moment 30 eurocent per liter. We gaan ervan uit dat de melkprijs niet verandert. Hij heeft op zijn boerderij 70 koeien die elke dag gemolken moeten worden. Een koe geeft gemiddeld 21,1 liter melk per dag als zij door de boer met de hand gemolken wordt. Uit onderzoek blijkt dat een koe die gemolken wordt door een melkrobot 10% meer melk geeft dan een koe die met de hand wordt gemolken door de boer. Boer Poelen wil weten hoeveel extra opbrengst hij per jaar (365 dagen) krijgt uit de verkoop van melk als hij overstapt op een melkrobot.
     
3p. 14. Bereken de extra opbrengst per jaar van boer Poelen. Rond je antwoord af op hele euro’s.
   

  


 

Een meisje of een jongen?
     
Veel vrouwen die in verwachting zijn van een baby vragen zich af of het een meisje of een jongen wordt. Er bestaan veel dubieuze methoden om daarachter te komen. Een voorbeeld daarvan is de al eeuwen oude Chinese conceptietabel, zie de volgende tabel.
     
  18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
jan M J M J M J M M J M J M J J J M J J M J M J M J M J J M
feb J M J M J J M J M J M J M M M J M J J M J M J M J M J J
maart M J M M J M J J J M J M M J J J J M J J M J M J M J M J
april J M J M M J J M M J M M M M M J M J M J J J J M J M J M
mei J M J M J J M M M M M J M M M M M M J M J J M J M J J M
juni J J J M M M J J J M M J M M M M M M M J M M J M J M J M
juli J J J M M J J M M J J J M M M M M M M M J M J J M J M J
aug J J J M J M M J J J J J M M M J M J M J M J M J J M J M
sept J J J M M J M J M J J J M M M M M M J M J M J M J J M J
okt J J M M M J M J M J J M M M M M M M J J M J M J M J J M
nov J M J M M J M J M M M M J M M M J J J M J M J M J J M J
dec J M J M M M M J M J M M J J J J J J J J M M M J M J M J
     
Met deze tabel zou je als volgt kunnen bepalen of het een jongen of een meisje wordt: kies de maand van de conceptie (verticaal) en de leeftijd van de moeder (horizontaal) op het moment van de conceptie. In het bijbehorende vakje staat de M voor een meisje en de J voor een jongen. Volgens een website voorspelt de tabel in 90% van de gevallen correct of het een jongen of een meisje wordt.

Twee zwangere vrouwen hebben nauwkeurig het moment van conceptie vastgesteld. Voor de ene vrouw was dat in de maand maart en haar leeftijd was toen 23 jaar. Voor de andere vrouw was dat in februari en haar leeftijd was toen 25 jaar. De twee vrouwen gebruiken de Chinese conceptietabel om het geslacht van hun baby te voorspellen. Ga ervan uit dat de tabel inderdaad in 90% van de gevallen correct voorspelt.
     
3p. 15. Bereken dan de kans dat de baby’s alle twee jongens zijn.
   

  
Een vrouw die gedurende haar leven vijf kinderen heeft gekregen onderzoekt of de Chinese conceptietabel klopt voor haar vijf kinderen. In een discussieforum op internet klaagt de vrouw erover dat de Chinese conceptietabel het bij alle vijf haar kinderen mis had. Als de 90%-claim van de website correct is, zo redeneerde de vrouw, dan zou er een behoorlijk grote kans moeten zijn dat de tabel het bij ten minste vier van de vijf kinderen goed zou hebben.
     
4p. 16. Bereken deze kans.
   

  
Er bestaat een verband tussen het geslacht van de baby en de leeftijd van de moeder op het moment van de geboorte van het kind. In onderstaande figuur is het aantal jongens per 1000 meisjes uitgezet tegen de leeftijd van de moeder.
     

     
De grafiek in deze figuur is het resultaat van een groot onderzoek waarin in totaal 11 093 182 geboortes werden geteld. We kijken in deze figuur bijvoorbeeld naar de leeftijdsklasse 20-24 jaar. We zien dat van de baby’s van wie de moeder bij de geboorte in deze leeftijdsklasse zit, er ongeveer 1058 jongetjes per 1000 meisjes worden geboren. De kans op een jongen is voor een willekeurige aanstaande moeder uit deze leeftijdsklasse dus 1058/2058 ≈ 0,514

De grafiek in de figuur daalt (bijna) overal. Dat betekent dat de verhouding tussen de aantallen jongens en meisjes (dus jongens : meisjes) (bijna) altijd afneemt naarmate de leeftijd van de moeder toeneemt. Dus is de kans op een jongen voor een zwangere vrouw van 45 jaar of ouder kleiner dan voor een zwangere vrouw die jonger is dan 20 jaar.
Omdat de grafiek in de figuur snel daalt, lijkt het er op alsof het verschil tussen beide kansen groot is.
     
5p. 17. Laat met een berekening zien dat het verschil tussen beide genoemde kansen klein is. Leg ook uit waarom de figuur de indruk wekt dat dit verschil groot is.
   

  
Het getal 2 347 092 in de figuur helemaal rechts geeft aan dat er 2 347 092 kinderen zijn geboren van wie de moeder bij de geboorte van het kind in de leeftijdsklasse 20-24 jaar zit. Met behulp van bovengenoemde verhouding 1058/2058 kunnen we het aantal jongens in die groep berekenen.
Door alle gegevens uit de figuur te gebruiken, kunnen we ook de verhouding jongens : meisjes in de gehele onderzochte groep van 11 093 182 kinderen berekenen. Deze verhouding is (ongeveer) 1056 :1000.
     
5p. 18. Laat deze berekening zien.
   

  


 

Studieschuld.
     
Het Centraal Bureau voor de Statistiek (CBS) houdt bij hoeveel studenten er zijn in het wetenschappelijk onderwijs in Nederland. De volgende tabel geeft daar informatie over.
     
studiejaar mannen vrouwen
1991-1992 98272 75281
1992-1993 97784 76739
1993-1994 97270 78052
1994-1995 95256 78372
1995-1996 91310 75959
1996-1997 83850 70226
1997-1998 80472 68014
1998-1999 79347 68524
1999-2000 80113 70631
     
Iemand trekt uit deze tabel de volgende twee conclusies:
1. Het aantal vrouwelijke studenten was in het studiejaar 1999-2000 ruim 6 procent lager dan in het studiejaar 1991-1992.
2. Het aandeel van de vrouwelijke studenten was in het studiejaar 1999-2000 groter dan in het studiejaar 1991-1992.
     
4p. 19. Onderzoek voor elk van deze conclusies of deze juist is of niet.
     
Lenneke was een van die studenten. Zij heeft haar studie psychologie in september 2002 succesvol afgerond. Tijdens haar studie heeft zij geld geleend van de IBG (Informatie Beheer Groep). In de loop van 2004 kreeg zij van de IBG het zogenoemde Bericht Terugbetalen. Daaruit komt het volgende citaat.
     
 
Citaat
Geachte mevrouw,
Volgens onze gegevens moet u per 1 januari 2005 beginnen met de
terugbetaling van uw studieschuld. Op 1 januari 2005 bedraagt deze schuld
3011 euro.
U kunt uw schuld ineens betalen, maar u mag dit ook in maandelijkse termijnen
doen. In uw situatie is deze maandelijkse termijn vastgesteld op 45,41 euro en
dit bedrag zal op de laatste dag van iedere maand van uw rekening worden
afgeschreven.
Bij het terugbetalen berekent de IBG een rente van 3,73% op jaarbasis over de
schuld die overblijft.
     
Een rente van 3,73% per jaar betekent een rente van (ongeveer) 0,3% per maand.
     
4p. 20. Laat met behulp van een berekening zien dat dit klopt.
   

  
Lenneke besloot destijds om vanaf januari 2005 elke maand 45,41 euro af te lossen. De hoogte van haar schuld Sn na n maanden voldoet dus aan de volgende recurrente betrekking (Een recurrente betrekking wordt ook wel recursieformule of recursievergelijking genoemd):
Sn+1 = 1, 003 • Sn − 45,41 met S0 = 3011
Bij de Oudejaarsloterij van december 2005 wint Lenneke 2500 euro. Zij besluit dit bedrag op 1 januari 2006 voor haar aflossing te gebruiken.
     
4p. 21. Heeft Lenneke op 2 januari 2006 nog schulden bij de IBG? Licht je antwoord met een berekening toe.
   

  
De schuld van Lenneke is ontstaan in de periode van begin september 2001 tot en met eind september 2002. Tijdens deze 13 maanden leende zij elke maand een bedrag van 211,09 euro.
De IBG hanteert de regel dat een schuld pas na enkele jaren hoeft te worden afgelost. Maar tot het begin van het aflossen (de aanloopfase) moet er wel elke maand rente worden betaald. Deze rente wordt aan de schuld toegevoegd.
Tijdens de jaren 2001 en 2002 berekende de IBG over de schuld een rente van 0,3% per maand, steeds ingaande in de maand nadat de bedragen waren uitgekeerd. Dat betekent dus dat op 31 oktober 2001 voor het eerst rente werd berekend.
Op 1 oktober 2002, toen Lenneke net was gestopt met lenen, bedroeg de studieschuld van Lenneke:
211,09 + 211,09 • 1,003 + 211,09 • 1,0032 + ...  ≈   2794,11 euro.
     
4p. 22. Toon met de somformule voor meetkundige rijen aan dat dit bedrag van 2794,11 euro klopt
   

  


 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. P(1895) = (264 • 1895 - 2476657)/(1895 - 1767) = 185
P(1995) = (264 • 1995 - 2476657)/(1995 - 1767) = 219
Er zijn dus 219 - 185 = 34 soorten ontdekt.
   
2. Het verschil tussen de formules is  nul als P = G
voer in de GR in:  Y1 = (264X - 476657)/(X-1767)  en  Y2 = 218(1-0,9799^(X-1798))
Kijk nu bij TABLE wanneer die gelijk zijn.
Kies bijv. Tblstart = 1930 en DTbl = 1
Dat geeft  (afgerond)  t = 1938 (beiden 205 soorten)  en t = 1941 (beiden 206 soorten) en t = 1942 (beiden 206 soorten) en t = 1944 (beiden 207 soorten) en t = 1945 (beiden 207 soorten)
   
3. G(2009) = 218(1 - 0,97992009-1798 ) = 215
Vul een erg groot getal voor t in, dan komt er uit  G = 218
Er zullen dus nog 218 - 215 = 3 soorten ontdekt worden.
   
4. vul bijv. in  a = 121,1  en  t = 1895 en  G = 187.
Die G is een afgerond getal, dus zal hebben gelegen tussen 186,5 en 187,5
Dat geeft  187,5 = √(121,2 • 1895 + b)
 ⇒  187,52 = 121,2 • 1895 + b
 ⇒  35156,25 = 229674 + b
 ⇒  b = 35156,25 - 229674 = -194517,75 

De andere grens geeft  186,5 = √(121,1 • 1895 + b)
 ⇒  186,52 = 121,1 • 1895 + b
 ⇒  34782,25 = 229674 + b
 ⇒  b = 34782,25 - 229674 = -194891,75 

De waarde van b zal daar tussenin liggen.
(het kan natuurlijk ook via de functie intersect van de GR)
   
5.

  Er is sprake van een normale verdeling omdat de punten ongeveer op een rechte lijn liggen.
   
6.

  Lees bij 50% het gemiddelde af:  ongeveer 9,3

Lees bij 84%  het gemiddelde plus de standaarddeviatie af:  ongeveer 11,3
De standaarddeviatie is dus ongeveer 11,3 - 9,3 = 2,0
   
7. Voor  één jongen geldt de klokvorm hiernaast.
De kans op een hogere score is  normalcdf(9.94, 1000..., 7.4, 2.0) = 0,102

De kans dat beide jongens zo'n score hebben is dan 0,102 • 0,102 = 0,01.

   
8. De gemiddelde score is ook normaal verdeeld.
Het gemiddelde ervan is 8
De standaarddeviatie ervan is  2/√100 = 0,2
Minder dan 0,1 afwijking vanaf 8,0 betekent een score tussen 7,9 en 8,1.
Normalcdf(7.9, 8.1, 8, 0.2) = 0,38
   
9. De klokvorm hiernaast geldt.
Dus is 0,77 = normalcdf(0, 8.85, 7.3, ?)

Y1 = 0,77
Y2 = normalcdf(0, 8.85, 7.3, X)
intersect geeft X = σ =  2,1

   
10. aflezen:
in 1975:  91000 bedrijven en  23 dieren per bedrijf:  Dat zijn 91000 • 23 = 2093000 dieren
in 2003:  25000 bedrijven en 59 dieren per bedrijf:  Dat zijn  25000 • 59 = 1475000 dieren.
dus in 2003 was het totaal aantal dieren kleiner dan in 1975.
   
11. In 2000: 51 dieren per bedrijf en in 2003: 59 dieren per bedrijf; een toename van 8 dieren per bedrijf.
Dat is per jaar 8/3 = 2,7 dieren per bedrijf.
In 1985: 35 dieren per bedrijf en in 2000:  51 dieren per bedrijf; een toename van 16 dieren per bedrijf
Dat is per jaar  16/15 = 1,1 dieren per bedrijf.
Dat is niet in tegenspraak met de grafiek, omdat in de grafiek de schaal van de x-as op het eind anders is dan in het begin. Aan het eind is de x-as meer "uitgerekt" en lijkt de grafiek daardoor minder snel te stijgen.
   
12. model 1.
Een rechte lijn door de punten (2002, 90) en (2005,83)
Helling is  (83 - 90)/(2005-2002 = -21/3
Tussen 2005 en 2015 is Dx = 10, dus dat zou een afname van 10 • 21/3 = 231/3% geven
In 2015 zou er dan  83 - 231/3 = 59,7%  in de wei komen.

model 2.
De factor tussen 2002 en 2005 is  83/90 = 0,9222 in drie jaar.
Per jaar is de factor dan  0,92221/3 = 0.97337
Kies als beginwaarde 2005, dan is de waarde in  2015 gelijk aan  83 • 0,9733710 = 63,3%
   
13. Als het lineair blijft dalen, dan zal het op den duur onder 0% komen en dat kan natuurlijk niet. Bij model 2 blijft het percentage altijd boven de 0%.
   
14. zonder robot ;
70 • 21,1 = 1477 liter, en dat levert op 1477 • 0,30 = 443,10 euro per dag.
in een jaar is dat 365 • 443,10 = 161731,50 euro

met robot:
21,1 • 1,1 = 23,21 liter per koe, dus 23,21 • 70 = 1624,70 liter per dag., en dat levert 1624,70 • 0,30 = 487,41 euro per dag. Per jaar is dat 365 • 487,41 = 177904,65 euro

de extra opbrengst is dus  177904,65 - 161731,50 = 16173 euro per jaar.
   
15. Uit de tabel: De eerste vrouw een meisje en de tweede een jongen.
De kans op een jongen bij de eerste vrouw is 0,1 en bij de tweede 0,9
De kans op twee jongens is dan 0,1 • 0,9 = 0,09
   
16. P(tenminste 4 goed) = P(4 goed) + P(5 goed)
P(5 goed) = 0,95 = 0,59049
P(4 goed) = 0,94 • 0,1 • 5 = 0,32805
Samen geeft dat een kans van 0,32805 + 0,59049 = 0,91854

(het kan ook binomiaal P(X ≥ 4) = 1 - P(X ≤ 3) = 1 - binomcdf(5, 0.9,3) = 0,91854)

   
17. Voor een vrouw van ouder dan 44 zijn er 1046 jongens bij 1000 meisjes, dus
1046 jongens van de 2046 kinderen. Dat geeft voor de kans op  een jongen 1046/2046 = 0,5112
Voor een vrouw jonger dan 20 jaar is de kans op een jongen 1061/2061 = 0,5148
Dat is inderdaad maar een klein verschil (0,0036)
Het verschil lijkt groot omdat de verticale as begint bij 1045. Je ziet eigenlijk alleen het stuk tussen 1045 en 1065 "uitvergroot"
   
18. Het aantal jongens in die leeftijdsklasse is  1058/2058 • 2347092 = 1206620
Voor de andere leeftijdsklassen geldt op dezelfde manier:
<20:  1061/2061 • 287530 = 148020
25-29:  1056/2056 • 4014600 = 2061974
30-34:  1056/2056 • 2736543 = 1405540
35-39: 1053/2053 • 1275284 = 654103
40-44:  1053/2053 • 400116 = 205223
>45:  1046/2046 • 32017 = 16368
Optellen geeft 5697848 jongens van de 11093183.
Dat is verhouding  5697848/11093183 = 0,514
1056/2056 = 0,514 dus dat klopt.
   
19. 1999-2000:  70631 vrouwen  en  1991-1992:  75281 vrouwen.
dat is een afname van 4650 vrouwen en dat is 4650/75281 • 100% = 6,18% dus conclusie 1 klopt.

1999-2000: 70631 vrouwen van de 70631 + 80113 = 150744 studenten is aandeel van 70631/150744 = 0,468
1991-1992: 75281 vrouwen van de 75281 + 98272 = 173553 studenten is aandeel 75281/173553 = 0,434
Het aandeel is toegenomen dus conclusie 2 is juist.
   
20. 3,73% rente betekent een groeifactor van  1,0373 per jaar.
Per maand is dat een groeifactor  1,03731/12 = 1,003056
Groeifactor 1,003056 betekent rente  0,3056%
   
21. Pak je GR:  MODE - seq en dan Y=
nmin = 0
u(n) = 1,003 • u(n-1) - 45,41
u(nmin) = 3011
Bij 1 januari 2006 hoort n  = 12 dus kijk in  TABLE bij n = 12.
Daar staat 2567,20
Dat betekent dat ze, als ze nog 2500 euro aflost, nog steeds 567,20 schuld heeft.
   
22. De beginwaarde is 211,09
De reden (vermenigvuldigfactor) is 1,003
Bij 1 oktober hoort n = 12.
De volgende term in de rij zou zijn  211,09 • 1,00313 = 219,47
De somformule geeft dan:  S = (219,47 - 211,09)/(1,003 - 1) = 2794,11