| VWO WA1, 2008 - II | ||
| Zes gooien | ||||||||||||||
|
Bij sommige spelletjes moet een speler eerst met een dobbelsteen een zes gooien voordat hij verder mag spelen. Soms gooit zo’n speler al in de eerste worp een zes, maar soms gooit hij bijvoorbeeld pas in de 10e worp een zes. In onderstaande tabel zie je een begin van een overzicht van de kansen om pas na een bepaald aantal worpen de eerste zes te gooien. Deze kansen zijn afgerond op vier decimalen. |
||||||||||||||
|
||||||||||||||
|
In de tabel zie je bijvoorbeeld dat de kans om pas in de 4e worp de eerste zes te gooien afgerond 0,0965 is. |
||||||||||||||
| 4p. | 18. | Bereken de kans om pas in de 7e worp de eerste zes te gooien. | ||||||||||||
|
De kansen in
tabel 4 vormen een meetkundige rij. Pn = 5/6 • Pn - 1, met P1 = 1/6 Hierbij is Pn de kans om de eerste zes te gooien bij de n-de worp. In plaats van deze recursieve formule kan voor deze rij ook een directe formule worden opgesteld. |
||||||||||||||
| 3p. | 19. | Geef de directe formule voor Pn . | ||||||||||||
|
De verwachtingswaarde E van het aantal worpen dat nodig is om de eerste zes te gooien kan worden berekend met de formule: E = 1• P1 + 2 • P2 + 3 • P3 + 4 • P4 +... Deze berekening gaat oneindig ver door. Je kunt de waarde van E benaderen door de berekening na een aantal termen te stoppen. De uitkomst die je krijgt door te stoppen na n termen, noemen we Sn. Hiervoor geldt dus de formule: Sn = 1 • P1 + 2 • P2 + 3 • P3 + ... + n • Pn Berekend kan
worden dat S30 ≈ 5,8483 . |
||||||||||||||
| 4p. | 20. | Bereken S31 | ||||||||||||
| UITWERKING | ||||
| Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten. | ||||
| 1. | Het moet
toenemen van 14800 naar 17000. Dat is een toename van 2200 en dat is 2200/14800 • 100% = 15% |
|||
| 2. |
|
|||
| 3. | C = (1,544 + 0,245 • log(50))9 = 1,969 = 427,36 uren | |||
| 4. | 950 =
(1,544 + 0,245 • logK)9 algebraïsch: 1,544 + 0,245 • logK = 9501/9 ≈ 2,14 ⇒ 0,245log(K) ≈ 0,598 ⇒ log(K) ≈ 2,442 ⇒ K ≈ 102.442 ≈ 276,44 miljoen (maar het mag ook met intersect van de GR natuurlijk...) |
|||
| 5. | Stijging
met 4% betekent vermenigvuldigen met groeifactor 1,04. Als de kosten in 2003 K waren, dan geldt er: 62,7 = K • 1,044 ⇒ K = 53,596 Dat geeft C = (1,544 + 0,245 • log(53,596))9 = 442 uren. |
|||
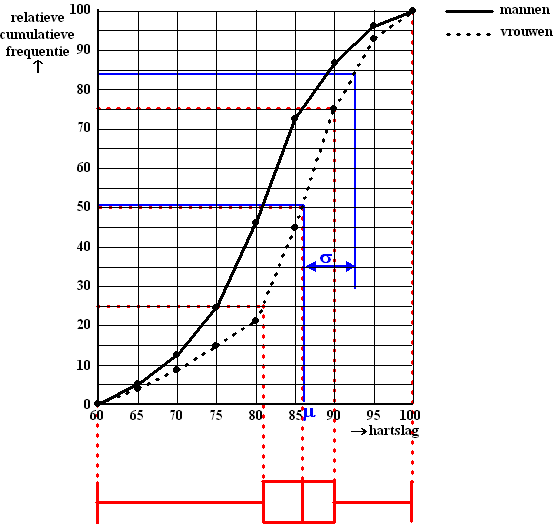
| 6+7 | Boxplot door de rode
lijnen te tekenen
Gemiddelde aflezen bij 50%:
μ
= 86 |
 |
||
| 8. |
98 is dan 50% van haar maximale
hartslag. Dus de maximale hartslag is 196. |
|||
| 9. | 220 -
0,9l = 214 - 0,8l
⇒ 6 = 0,1l
⇒ l = 60 De leeftijd zal in de buurt van de 60 moeten liggen. Probeer: l = 57 geeft bij methode 1 hartslag 168,7 en bij methode 2 hartslag 168,4 en die zijn afgerond verschillend. l = 58 geeft bij methode 1 hartslag 167,8 en bij methode 2 hartslag 167,6 l = 59 geeft bij methode 1 hartslag 166,9 en bij methode 2 hartslag 166,8 l = 60 geeft bij methode 1 hartslag 166 en bij methode 2 hartslag 166 l = 61 geeft bij methode 1 hartslag 165,1 en bij methode 2 hartslag 165,2 l = 62 geeft bij methode 1 hartslag 164,2 en bij methode 2 hartslag 164,4 l = 63 geeft bij methode 1 hartslag 163,3 en bij methode 2 hartslag 163,6 en die zijn afgerond verschillend Conclusie: de leeftijden zijn 58, 59, 60, 61 of 62 jaar. Kies er maar twee uit. |
|||
| 10. | Er zijn
zes tegels met twee dezelfde symbolen en die komen allemaal 5 keer voor:
dat zijn 30 tegels. Er zijn 6 nCr 2 = 15 tegels met verschillende symbolen en die komen allemaal 6 keer voor: dat zijn 90 tegels. In totaal zijn er dus 90 + 30 = 120 tegels. |
|||
| 11. | Er zijn
nog 33 tegels zonder één of meer zonnen P( geen enkele tegel met zon(nen)) = 33/50 • 32/49 • 31/48 • 30/47 • 29/46 • 28/45 = 0,0696991 P(minstens één tegel met zon(nen)) = 1 - 0,0696991 ≈ 0,93. |
|||
| 12. | Geef speler D bijvoorbeeld 8 - 18 - 18 - 18 - 17 - 17 dan is zijn gemiddelde 16, maar zijn laagste score lager dan die van alle andere spelers. | |||
| 13. | Dit is
een binomiaal experiment met n = 25 en p = 1/3. P(X ≥ 12) = 1 - P(X ≤ 11) = 1 - binomcdf(25, 1/3, 11) = 0,0918 |
|||
| 14. | Jongens
langer dan 185: normalcdf(185, 100000, 181, 8) = 0,309 Meisjes langer dan 185: normalcdf(185, 100000, 169, 7) = 0,011 30 • 0,011 = 0,334 dus dat klopt redelijk. |
|||
| 15. | Er zijn
22 lange leerlingen en 72 niet-lange. Een mogelijkheid is LLLLLNNNNNNNNN, met kans: 22/94 • 21/93 • 20/92 • 19/91 • 18/90 • 72/89 • 71/88 • 70/87 • 69/86 • 68/85 • 67/84 • 66/83 • 65/82 • 64/81 = 0,0000642 Er zijn 14 nCr 5 = 2002 zulke mogelijkheden, dus de kans is 2002 • 0,0000642 = 0,128 of: |
|||
| 16. | meisjes:
normalcdf(405, 435, 449, 26) = 0,2498 dus dat zijn 0,2498 • 60 = 14,99
» 15 meisjes jongens: normalcdf(405, 435, 489, 27) = 0,0218 dus dat zijn 0,0218 • 60 = 1,3 » 1 jongen In totaal dus 15 + 1 = 16 leerlingen |
|||
| 17. | De
groeifactoren waren 29467/25597 = 1,151
en 33870/29467 = 1,149 en 39051/33870
= 1,153 Dat is allemaal ongeveer gelijk aan 1,15. Kies als beginhoeveelheid de waarde in 2005: 39051. Dan is de hoeveelheid in 2010 39051 • 1,155 ≈ € 78546 |
|||
| 18. | P(NNNNNNZ) = 5/6 • 5/6 • 5/6 • 5/6 • 5/6 • 5/6 • 1/6 = 0,0558 | |||
| 19. | Dat is
een formule van de vorm Pn = B • gn
g is de reden van de rij (het getal waarmee wordt vermenigvuldigd) en dat is 5/6. B is de waarde bij n = 0 en dat is P0 = P1/(5/6) = (1/6)/(5/6) = 1/5. Dus Pn = 1/5 • (5/6)n |
|||
| 20. | S31=
S30
+ 31
• P31
P31 = (5/6)30 • (1/6) = 0,000702 Dus S31 = 5,8483 + 31 • 0,000702 = 5,8701 |
|||