Nieuwe pagina 1

VWO WA1, 2001 - II

Vakkenkeuze

In het voorjaar van 1994 zijn bij een onderzoek naar vakkenkeuze 344 jongens en 493 meisjes ondervraagd die toen eindexamen deden.
Nederlands was voor iedereen verplicht. Havo-leerlingen moesten naast Nederlands nog tenminste 5 andere vakken kiezen. In de tabel hieronder is te zien door hoeveel procent van de ondervraagden de andere vakken zijn gekozen.

vak	jongens (in %)	meisjes (in %)
Duits	31,1	46,7
Engels	98,8	97,6
Frans	10,2	38,5
Aardrijkskunde	19,2	28,2
Geschiedenis	25,3	30,2
Economie	60,2	47,9
Handelswetenschappen	43,0	29,8
Wiskunde A	43,3	62,3
Wiskunde B	54,7	22,3
Biologie	23,5	45,2
Natuurkunde	57,6	17,0
Scheikunde	42,2	24,5
Tekenen	7,0	15,2
Maatschappijleer	2,9	4,5
Muziek	0,9	3,4
Handenarbeid	2,3	4,9
Textiele werkvormen	0,0	0,4
Spaans	0,0	0,6

Toon aan dat van de ondervraagde leerlingen meer meisjes dan jongens economie deden.

De meeste leerlingen hadden naast Nederlands 5 vakken gekozen. Sommige leerlingen hadden naast Nederlands 6 vakken gekozen. Geen van de leerlingen had naast Nederlands meer dan 6 vakken gekozen.

Bereken hoeveel procent van de ondervraagde meisjes een extra vak deed.

De onderzoekers vermoedden dat veel kandidaten ontevreden waren over hun huidige vakkenpakket. Bij het onderzoek werd ook gevraagd of je, als je opnieuw zou mogen kiezen, weer precies hetzelfde pakket gekozen zou hebben.
De leerlingen moesten daarbij aangeven wélke vakken ze zouden willen vervangen.
Voor enkele vakken staat het resultaat in de figuur hieronder. Bijvoorbeeld: van alle meisjes met wiskunde B zou ongeveer 21% dat vak achteraf liever niet hebben gekozen.

Aan de leerlingen die tenminste één ander vak gekozen zouden hebben werd ook gevraagd welk nieuw vak of welke nieuwe vakken ze zouden kiezen. In de figuur hieronder staat voor enkele vakken het resultaat. Bijvoorbeeld: van de meisjes die tenminste één ander vak gekozen zouden hebben zou ruim 25% wiskunde A kiezen. (Merk op dat veel leerlingen meer dan één nieuw vak zouden kiezen, waardoor het totaal zelfs over deze zes vakken al ver boven de 100% komt).

Er waren 127 jongens en 232 meisjes die tenminste één ander vak zouden kiezen.
Stel dat alle leerlingen het achteraf gewenste pakket hadden gekozen.

Onderzoek of dan nog steeds meer meisjes dan jongens economie zouden doen. Maak hierbij gebruik van de resultaten van vraag 1 en van de beide figuren hierboven.

Persoonlijke lening

Iemand heeft bij een bank een persoonlijke lening afgesloten van ƒ80000,-. Voor rente en aflossing betaalt hij aan het eind van elke maand een vast bedrag, namelijk ƒ720,-. De bank brengt hem 0,7% rente per maand over het restant van de lening in rekening.
L₀ is het beginbedrag: ƒ80000,-. L_t is het restant van de lening direct na het einde van de t^e maand. L_t berekent men als volgt:
Eerst wordt het restant van de lening na t - 1 maanden vermeerderd met de verschuldigde rente en daarna wordt de ƒ 720,- er van af getrokken.
In de tabel hieronder kun je voor de eerste paar maanden zien hoe groot het restant van de lening is aan het eind van elke maand. Er wordt bij alle bedragen gerekend in guldens.

	t = 0	t = 1	t = 2	t = 3	t = 4
L_t	80000	79840	79678,88	79516,63	79353,25

Bereken L₆.

Het maandbedrag van ƒ720,- bestaat voor een deel uit rente die betaald moet worden en voor een deel uit aflossing. Met de tabel hierboven kunnen we nagaan dat er aan het eind van de 1^e maand ƒ160,- van de lening wordt afgelost. Aan het eind van de 2^e maand wordt ƒ161,12 afgelost. De aflossing aan het eind van de t^e maand geven we aan met A_t. In de tabel hieronder zie je voor de eerste paar maanden hoe groot de aflossing is die er aan het eind van elke maand plaatsvindt.

	t = 1	t = 2	t = 3	t = 4
A_t	160,-	161,12	162,25	163,38

Omdat het restant van de lening steeds kleiner wordt, zal de aflossing A_t toenemen.
Het blijkt dat A_t exponentieel groeit.

Laat zien dat bij de waarden van A_t in de tabel hierboven sprake is van exponentiële groei.

Het is mogelijk deze exponentiële groei in een formule weer te geven. Deze formule ziet er als volgt uit:
A_t = 160 · 1,007^{t - 1}

Bereken na hoeveel maanden de aflossing voor het eerst groter is dan ƒ200,-

Aan de formule voor A_t is te zien dat er sprake is van een meetkundige rij. Om te berekenen hoeveel er na verloop van tijd in totaal is afgelost moet dus de som van een meetkundige rij bepaald worden.

Bereken hoe groot het bedrag is dat in totaal is afgelost aan het eind van de 60^e maand.

Geboorte

In de kansrekening gaat men er vaak van uit dat bij een geboorte de kans op een jongen even groot is als de kans op een meisje, namelijk 0,5. In werkelijkheid worden er iets meer jongens geboren dan meisjes. Bij elke geboorte is de kans op een jongen ongeveer 0,51.

Wanneer we bijvoorbeeld de kans willen berekenen dat een gezin met 4 kinderen bestaat uit 2 jongens en 2 meisjes dan kunnen we gebruik maken van de bovengenoemde 0,5. Maar we kunnen die kans ook berekenen met behulp van de bovengenoemde 0,51. De twee uitkomsten die we krijgen zijn niet even groot.

Bereken hoeveel beide uitkomsten van elkaar verschillen.

Ook bij de Europese vorstenhuizen is de kans dat een jongen wordt geboren 0,51. Toch zijn er bij de 500 geboortes die de afgelopen eeuwen bij de Europese vorstenhuizen plaatsvonden maar liefst 285 jongens geboren. De kans op zo'n groot aantal jongens is niet zo groot.

Bereken de kans dat er bij 500 geboortes minstens 285 jongens zijn.

De Nieuw-Zeelandse arts Grant heeft onderzocht of de kans op een jongen, en daarmee dus ook de kans op een meisje, afhangt van persoonlijkheidskenmerken van de moeder. Daartoe deelde zij in eerste instantie een onderzoeksgroep in drie verschillende categorieën in. De resultaten van dat onderzoek zie je in onderstaande tabel.

categorie:	meegaand	bescheiden	dominant
aantal geboortes:	4073	2048	4018
aantal meisjes:	2767	962	1257

10.

Bereken in 3 decimalen nauwkeurig voor de totale onderzoeksgroep hoe groot de kans is op een jongen.

Bovenstaand onderzoek was voor Grant aanleiding om verder te zoeken. In het vervolgonderzoek deelde zij de moeders in 5 categorieën in: zeer meegaand, meegaand, bescheiden, dominant en zeer dominant. Uit het vervolgonderzoek bleek dat de kans op een meisje bij een zeer meegaande moeder vijf keer zo groot is als de kans op een meisje bij een zeer dominante moeder.

Als de uitkomst van het vervolgonderzoek van Grant juist is, is de kans op een jongen bij een zeer dominante moeder, zo valt na te rekenen, groter dan 0,8. Dat betekent dat deze kans dus zeker niet gelijk kan zijn aan bijvoorbeeld 0,75.

11.

Laat door een berekening zien dat deze kans inderdaad niet gelijk kan zijn aan 0,75

Uit de uitkomst van Grants vervolgonderzoek mag je niet de conclusie trekken dat de kans op een jongen bij een zeer dominante moeder vijf keer zo groot is als bij een zeer meegaande moeder.

12.

Laat met behulp van een getallenvoorbeeld zien dat je die conclusie inderdaad niet mag trekken.


Kavelkosten

Een gemeente wil uitbreiden door het bouwen van een nieuwe wijk. De plaats waar de nieuwe wijk gebouwd zal worden is vastgesteld. Voordat de gemeente het uitbreidingsplan laat uitvoeren doet de gemeente onderzoek naar de kosten van het plan. Er zijn twee soorten kosten voor de gemeente:
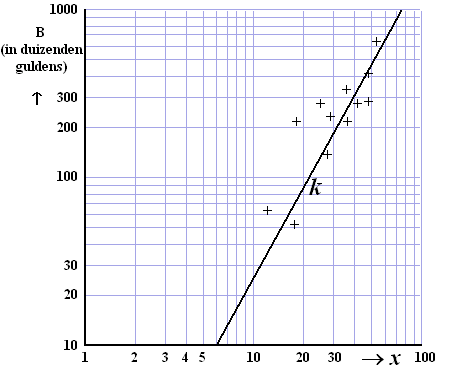
de kosten van aankoop van de grond. In deze situatie bedragen de kosten 170000 gulden per hectare (1 hectare = 10000 m²) de kosten van het bouwrijp maken. Dit betreft kosten voor de aanleg van bijvoorbeeld wegen, rioleringen en groenvoorzieningen. Deze kosten zijn hoger naarmate het aantal woningen dat per hectare gebouwd zal worden groter is.
In de figuur hieronder zijn kosten van diverse vergelijkbare projecten door middel van plusjes weergegeven. Zowel langs de horizontale as als langs de verticale as is een logaritmische schaalverdeling gebruikt. Hierbij is x het aantal woningen per hectare. B stelt voor de kosten per hectare van het bouwrijp maken in duizenden guldens. Op grond van de plusjes in de figuur is een grafiek (de lijn k in de figuur) getekend die het verband tussen x en B weergeeft. De lijn k beschrijft een theoretisch model waarmee B kan worden berekend. De werkelijke kosten bij de onderzochte projecten (de plusjes in de figuur) wijken soms aanzienlijk af van de kosten volgens dit model.



Kijk bijvoorbeeld maar naar de kosten van het project dat hoort bij x = 19

5p	13.	Onderzoek of de werkelijke waarde van B van dit project meer dan 100% afwijkt van de waarde van B volgens het model.

Voor x = 100 is de waarde van B volgens het model niet in de figuur af te lezen.

4p	14.	Geef voor x = 100 een schatting van de waarde van B volgens het model. Maak hierbij gebruik van de figuur hierboven. Licht je werkwijze toe.

Ga er in de rest van de opgave van uit dat B = 0,4 · x^1,8Neen aan dat de gemeente 30 woningen per hectare wil bouwen.

4p	15.	Bereken de kosten voor het bouwrijp maken die de gemeente dan per woning zal maken.

De totale kosten per woning die de gemeente maakt noemen we K. Voor het verband tussen K en x kan de volgende formule worden afgeleid: K = 0,4 · x^0,8 + ¹⁷⁰/_x Hierbij is K in duizenden guldens.

2p	16.	Toon dit aan.

De gemeente wil dat de kavelgrootte (dat wil zeggen de grondoppervlakte) voor alle woningen in de nieuwe wijk hetzelfde is. Bovendien wil men dat de totale kosten die de gemeente per woning maakt minimaal zijn.

5p	17.	Onderzoek bij welk aantal woningen per hectare de totale kosten die de gemeente per woning maakt minimaal zijn.


Schaatsrecords

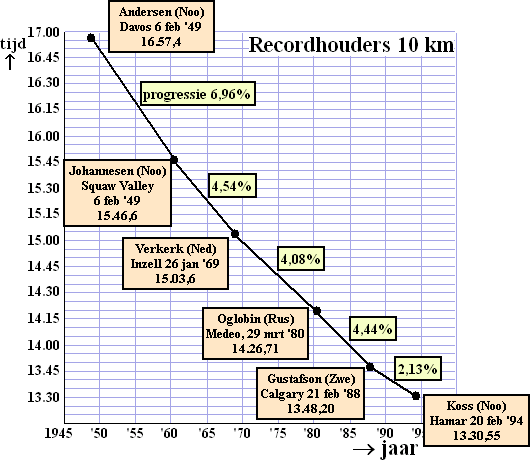
Als een schaatsrecord verbetert wordt verschijnen in de kranten vaak prachtige grafieken. In de figuur hieronder is weergegeven hoe de recordtijden op de 10 kilometer voor mannen zich in de loop der jaren ontwikkeld hebben. Voor het overzicht heeft men niet alle in deze periode behaalde wereldrecords vermeld.



Zo zien we dat Koss in 1994 een recordtijd van 13.30,55 reed. Dit houdt in dat de Noor de 10 kilometer aflegde in 13 minuten en 30,55 seconden. Tussen twee vermelde records staat steeds met hoeveel procent in die periode de recordtijd gedaald is. We noemen dat progressie. Nog niet vermeld in deze figuur is de recordtijd die Gianni Romme op 17 februari 1998 reed, namelijk 13.15,33.

3p	18.	Laat met een berekening zien dat dit een progressie van 1,88% betekent ten opzichte van het record van Koss uit 1994.

Stel dat dit record van Romme ook in figuur 4 zou staan.

5p	19.	Onderzoek of de grafiek tussen 1994 en 1998 minder steil zou dalen dan tussen 1969 en 1980.

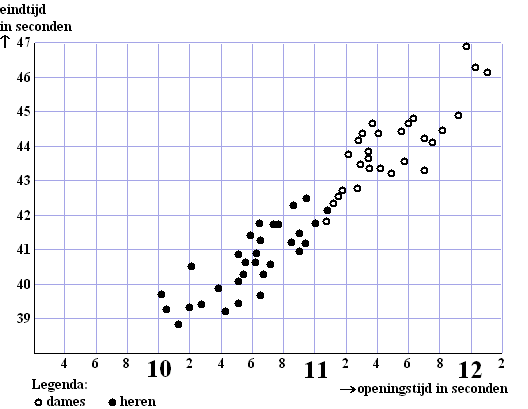
De grafiek hieronder is afkomstig uit een handboek voor wedstrijdschaatsen. In die grafiek is te zien dat bij wedstrijden op de 500 meter er bij benadering een lineair verband is tussen de tijd over de eerste 100 meter (de openingstijd) en de tijd over de hele rit (de eindtijd).



Een sportcommentator wil een lineaire formule hebben om op grond van de openingstijd een voorspelling van de eindtijd te berekenen. Hij tekent daartoe een rechte lijn in de figuur hierboven die zo goed mogelijk past bij al deze punten.

5p	20.	Teken in de figuur hierboven een dergelijke lijn en stel de bijbehorende formule op.


OPLOSSINGEN

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

1.	Jongens met economie: 60,2% van 344 = 207 Meisjes met economie: 47,9% van 493 = 236 Dus er zijn meer meisjes met economie.

2.	Als elk meisje precies vijf vakken zou hebben gekozen zou de rij percentages opgeteld 500% geven. De optelling levert 46,7 + 97,6 + ... + 0,4 + 0,6 = 519,2% Dat betekent dat 19,2% van de meisjes een extra vak heeft gekozen.

3.	Bij vraag 1 is berekend dat 207 jongens het vak economie hebben gekozen. In de eerste figuur is af te lezen dat 7,5% daarvan, ofwel 16 jongens liever een ander vak hadden gekozen. In de tweede figuur is af te lezen dat 34% van de 127 jongens die een ander vak hadden willen kiezen voor economie gekozen zouden hebben, dus dat zijn 43 jongens. Het aantal jongens met economie zou dan 207 - 16 + 43 = 234 zijn geweest. Dezelfde berekening voorde meisjes geeft 236 - 41 + 53 = 248 meisjes. Dus ook als alle leerlingen het achteraf gewenste pakket hadden gekozen zouden meer meisjes economie doen.

4.	Een rente van 0,7% per maand betekent een groeifactor van 1,007 per maand. L₅ = 1,007 • L₄ - 720 = 79188,72 L₆ = 1,007 • L₅ - 720 = 79023,04

5.	Er is sprake van exponentiële groei als de factoren tussen de opvolgende waarden steeds hetzelfde is. ^161,12/₁₆₀ = 1,007 en ^162,25/_161,12 = 1,007 en ^163,38/_162,25 = 1,007 De factor is vrijwel constant dus de groei is exponentieel.

6.	160 • 1,007^x-1 = 200 ⇒ 1,007^{x - 1} = 12,5 ⇒ x - 1 = ^log(12,5) /_log(1,007) = 31,989... ⇒ x = 32,989 Omdat A_t stijgt zal de aflossing voor het eerst groter zijn dan ƒ200,- na 33 maanden. (De oplossing van 160 • 1,007^x-1 = 200 kan ook gevonden worden door beide kanten in te voeren in de GR en INTERSECT te gebruiken).

7.	Op het eind van de 60^e maand is in totaal A₁ + A₂ + A₃ + ... + A₆₀ afgelost. Dat is 160 + 160 • 1,007 + 160 • 1,007² + ... + 160 • 1,007⁵⁹ Dit is een rekenkundige rij met b = 160 en reden r = 1,007 De som daarvan is S_n = b• (1 - rⁿ) /(1 - r) = 160 • (1 - 1,007⁶⁰) / (1 - 1,007) = 11879,69

8.	1^e opl.	P(2 meisjes en 2 jongens) = (4 nCr 2) • P(MMJJ) In het ene geval geeft dat 6 • 0,5⁴ = 0,3750 In het andere geval 6 • 0,49² • 0,51² = 0,3747 Het verschil is 0,0003
	2^e opl.	BINOMPDF (4 , 0.5 , 2) = 0,375 en BINOMPDF (4 , 0.51 , 2) = 0,3747 Het verschil is 0,0003

9.	Het aantal jongens A is binomiaal verdeeld met n = 500 , p = 0,51. P(minstens 285) = P(A ≥ 285) = 1 - P(A ≤ 284) = 1 - BINOMCDF (500 , 0.51 , 284) = 1 - 0,9959 = 0,0041

10.	Het totale aantal geboorten is 4073 + 2048 + 4018 = 10139 Het totale aantal meisjes is 2767 + 962 + 1257 = 4986 De kans op een meisje is dus ⁴⁹⁸⁶/₁₀₁₃₉ = 0,4917 De kans op een jongen is 1 - 0,4917 = 0,5083 = 0,508 (op drie decimalen)

11.	Stel dat de kans op een jongen bij een zeer dominante moeder 0,75 is. Dan is de kans op een meisje 0,25 De kans op een meisje bij een meegaande moeder zou dan 5 • 0,25 = 1,25 moeten zijn. Maar dat kan niet want een kans kan nooit groter dan 1 zijn. Conclusie: een kans van 0,75 bij een zeer dominante moeder is niet mogelijk.

12.	Stel dat de kans op een jongen bij een zeer dominante moeder 0,9 is Dan is de kans op een meisje bij een zeer dominante moeder 1 - 0,9 = 0,1 Dan is de kans op een meisje bij een zeer meegaande moeder 5 • 0,1 = 0,5 Dan is de kans op een jongen bij een zeer meegaande moeder 1 - 0,5 = 0,5 0,9 is niet 5 keer zo groot als 0,5.

13.	De modelwaarde en de werkelijke waarde van B kunnen worden afgelezen bij x = 19 De modelwaarde is de hoogte van lijn k en is ongeveer B = 85 De werkelijke waarde is de plaats van het + teken en is B = 210 De werkelijke waarde is meer dan tweemaal de modelwaarde en wijkt dus meer dan 100% af.

14.	Verleng de grafiek van k tot bij x = 100 Verleng de verticale schaal als volgt: De afstand tussen 10 en 20 is hetzelfde als tussen 1000 en 2000. Dus het punt 2000 op de y-as is te tekenen. De afstand tussen 10 en 15 is hetzelfde als tussen 1000 en 1500. Dus het punt 1500 op de y-as is te tekenen. Het snijpunt van k met de verticale lijn x = 100 blijkt ongeveer B = 1600 te zijn.

15.	x = 30 ⇒ B = 0,4 • 30^1,8 = 182,338 (duizenden guldens) Per hectare zijn de kosten voor bouwrijp maken ƒ182338,- Per woning is dat ¹⁸²³³⁸/₃₀ = ƒ6078,-

16.	De totale kosten per hectare zijn B + 170 (in duizenden guldens) Per hectare komen x woningen, dus voor de kosten K per woning geldt:

17.	Voer de functie K uit de vorige vraag in in de grafische rekenmachine. Gebruik CALC - MINIMUM om het minimum te bepalen. Dat geeft x = 32,66 en y = 11,71 x is een aantal huizen en moet dus een geheel getal zijn. x = 32 geeft K = 11,7125 x= 33 geeft K = 11,7110 Voor minimale kosten moet de gemeente dus 33 woningen per hectare bouwen.

18.	De tijd van Koss was 13 minuten en 30,55 seconden, en dat is 810,55 seconden De tijd van Romme was 13 minuten en 15,33 seconden en dat is 795,33 seconden. Romme reed 810,55 - 795,33 = 15,22 seconden sneller Dat is (^15,22/_810,55) • 100% = 1,88% progressie.

19.	Tussen 1969 en 1980 is de daling 63,6 - 26,71 = 36,89 seconden. Dat is ^36,89/₁₁ = 3,35 seconden per jaar Tussen 1994 en 1998 is de daling 15,22 seconden (zie vraag 18) en dat is ^15,22/₄ = 3,81 seconden per jaar De grafiek daalt tussen 1994 en 1998 steiler dan tussen 1996 en 1980.

20.	Een lijn die redelijk bij de punten past gaat bijv. door (10 , 39) en (11.8 , 45) Het hellinggetal van deze lijn is ^{(45 - 39)}/_{(11.8 - 10)} = 3,33 De vergelijking wordt dan y = 3,33x + b Vul bijv. het punt (10,39) in. Dat geeft 39 = 3,33 • 10 + b ⇒ b = 5,7 De formule is dan y = 3,33x + 5,7 Het kan ook met de GR: Zet in lijst 1 (STAT -EDIT) de getallen 10 en 11,8 en ernaast in lijst 2 de getallen 39 en 45. LinReg (L₁, L₂) geeft de gevraagde formule.