| UITWERKING |
| |
|
| Het
officiële (maar soms beknoptere) correctievoorschrift kun je
HIER
vinden. Vooral handig voor de onderverdeling van de punten. |
| |
|
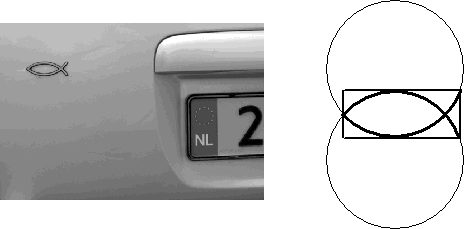
| 1. |
De
oppervlakte van de rechthoek is 10 • 30 = 300
De twee halve cirkels zijn samen een hele cirkel met straal 5, en die
heeft oppervlakte
π • 52 = 25π
Samen is dat 300 + 25π =
379 cm2 |
| |
|
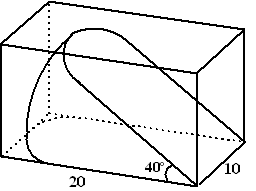
| 2. |
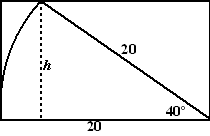
Het vooraanzicht
is als hiernaast.
Daarin zie je dat sin40º = h/20
Dus h = 20 • sin40º = 12,9
Het doosje moet dus minstens 13
cm hoog zijn. |
 |
| |
|
| 3. |
V =
5000 en h = 8 invullen geeft 5000 = 1/6π
• 83 + 1/8π2
• d • 82 + 1/4π
• d2 • 8
dat geeft 268,08257 + 78,9568d + 6,2832d2
= 5000 dus 6,2832d2 + 78,9568d -
4731,91743 = 0
ABC formule met a = 6,2832 en b = 78,9568 en
c = -4731,91743 geeft d = 21,87 (of d =
-34,4)
(het kan natuurlijk ook met intersect van de GR)
Als de hoogte 8 is, is de straal van de cirkel die de zijkanten vormt 4.
De totale lengte wordt dan 21,87 + 2 • 4 = 29,87
Als de plank 350 cm is, passen er 350/29,87 = 11,7 kazen naast
elkaar.
Dat zijn dus 11 kazen.
|
| |
|
| 4. |
V = 1/6π
• h3 + 1/8π2
• 0 • h2 + 1/4π
• 0 • h
V = 1/6π
• h3
Maar h = 2r dus daar staat V = 1/6π
• (2r)3 = 1/6π
• 8r3 = 8/6π
• r3 = 4/3πr3 |
| |
|
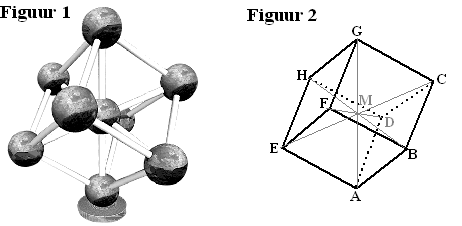
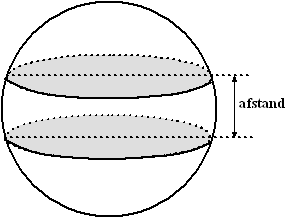
| 5. |
De
oppervlakte van één bol is 4 •
π • 92
= 324π. Dus 9 bollen hebben oppervlakte 9 •
324π = 2916π
Van de 8 bollen aan de rand lopen 4 buizen naar een andere bol. Dat zijn
8 • 4 = 32 aanhechtingspunten op die bollen.
Van de middenbol lopen 8 buizen naar de andere bollen. In totaal zijn er
dus 32 + 8 = 40 aanhechtingspunten.
Elk heeft oppervlakte 7m2 dus in totaal is dat 40 • 7 = 280 m2
De oppervlakte die overblijft voor de bekleding is dan 2916p
- 280 - 750 = 8130,88 m2
|
| |
|
| 6. |
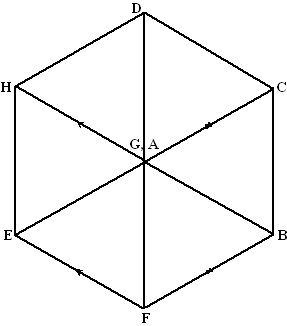
F ligt recht onder
G zodat GF = GH = GC.
Teken EF evenwijdig een HG en even lang.
Dat geeft punt E.
Teken FB evenwijdig aan AC en even lang.
Dat geeft punt B
Samen geeft dat het bovenaanzicht hiernaast. |
 |
| |
|
| 7. |
De oppervlakte is
240, dus
πr2 = 240
Dan is r2 = 240/π = 76,39 dus r =
√76,39 = 8,74
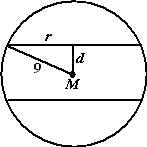
In het vooraanzicht hiernaast zie je dat Pythagoras geeft dat 92
= 8,742 + d2 dus d2
= 92 - 8,742 = 4,61
dan is d = √4,61 = 2,146
De afstand tussen de verdiepingen is dan 2 • 2,146 =
4,3 m. |
 |
| |
|
| 8. |
f(x)
= 2sinx + 2sinx • sinx = 2sinx + 2sin2x
Met de kettingregel: f '(x) = 2cosx + 2 •
2sinx • cosx = 2cosx(1 + 2sinx)
of direct met de productregel:
f '= 2cosx(1 + sinx) + 2sinx • cosx
= 2cosx + 2cosx sinx + 2sin cosx = 2cosx
+ 4sinxcosx
= 2cos(1 + 2sinx) |
| |
|
| 9. |
f
'(x) = 0 ⇒ cosx = 0
of 1 + 2sinx = 0
cosx = 0 geeft x = 1/2π
1 + 2sinx = 0 ⇒ 2sinx = -1
⇒
sinx = -1/2 ⇒
x = -1/6π
of x = 11/6π
en die laatste is de goede.
minimum: f(11/6π)
= 2sin11/6π
• (1 + sin11/6π)
= -1/2
maximum: f(1/2π)
= 2sin1/2π
• (1 + sin1/2π)
= 4 |
| |
|
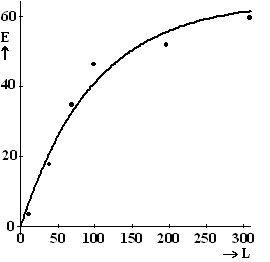
| 10. |
Bij L
= 100 lees je ongeveer af E = 48.
Volgens de formule moet het zijn E = 64 • (1 - 0,60,02 • 100)
= 40,96 dus ongeveer 41.
Het verschil is 48 - 41 = 7 larven. |
| |
|
| 11. |
Als L
groter wordt gaat 0,60,02L naar nul toe.
Dan gaat 1 - 0,60,02L naar 1 toe
Dan gaat 64 • (1 - 0,60,02L) naar 64 toe
De grenswaarde van E zal 64
zijn. |
| |
|
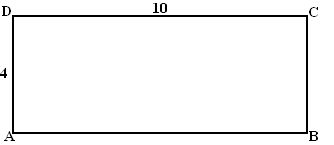
| 12. |
1/x
+ 1 = 4/3
⇒
1/x = 1/3
⇒ x = 3
De omtrek is dan 3 + 4/3 + 3 + 4/3
= 82/3.
|
| |
|
| 13. |
De
oppervlakte is y • x
Dat is (1/x + 1) • x =
1/x • x + 1 • x = 1 +
x
Omdat x > 0 is dit altijd groter dan 1 |
| |
|
| 14. |
f(x)
= x-1 + 1
f '(x) = -x-2
f '(x) = -1/2 ⇒
-x-2 = -1/2 ⇒
x-2 = 1/2 ⇒
1/x2 =
1/2 ⇒
x2 = 2 ⇒
x = √2 (x = -√2
kan niet)
Dus de x-coördinaat van B is √2. |
| |
|
| 15. |
In
driehoek MGE: EG2 + GM2 = EM2
EG = p
GM = r - 2
EM = r
Dat geeft p2 + (r - 2)2 =
r2 ⇒ p2
+ r2 - 4r + 4 = r2
⇒ p2 + 4 = 4r ⇒
r = 1/4(p2
+ 4) = 1/4p2
+ 1 |
| |
|
| 16. |
p2
- 20p + 116 - 8(1/4p2 + 1) = 0
⇒ p2 - 20p +
116 - 2p2 - 8 = 0
⇒ -p2 - 20p +
108 = 0
⇒ p2 + 20p -
108 = 0 |
| |
|
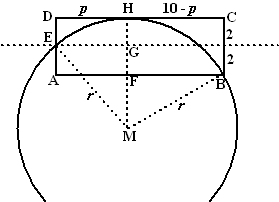
| 17. |
p2
+ 20p - 108 = 0
ABC formule met a = 1, b = 20 en c = -108
geeft p = 4,42 (en ook p = -24,42 maar die klopt
niet)
r = 1/4p2
+ 1 = 1/4
• 4,422 + 1 = 5,9
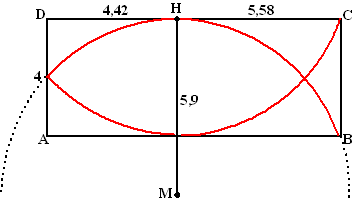
Teken H zodat DH = 4,42.
Teken recht daaronder M zodat HM = 5,9
Teken cirkelbogen met straal MH en je krijgt de figuur hiernaast. |
 2 2 |
| |
|
| 18. |
f(x)
= 4 • (9 + 3x)0,5
Met de kettingregel: f '(x) = 0,5 • 4 • (9 + 3x)-0,5
• 3 = 6(9 + 3x)-0,5
f '(9) = 6(9 + 3 • 9)-0,5 = 6 • 36-0,5 = 6
• 1/6 = 1 |
| |
|
| 19. |
de
vergelijking van m is (omdat de richtingscoëfficiënt 1 is):
y = x + b
m gaat door (9, 24) dus 24 = 9 + b dus b
= 15. En daarom is B = (0,15)
f(0) = 4 • √(9 + 3 • 0) = 12 dus
A = (0, 12)
Kies als basis van driehoek ABS zijde AB; die is 15 - 12 = 3
De hoogte is dan de afstand van S tot de y-as en die is 9.
De oppervlakte is dan 0,5 • 3 • 9 = 13,5 |
| |
|
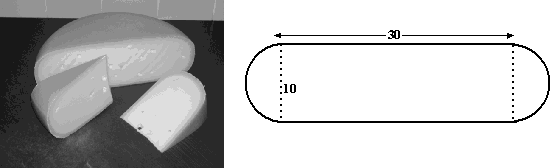




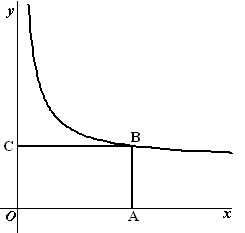
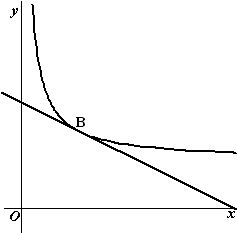
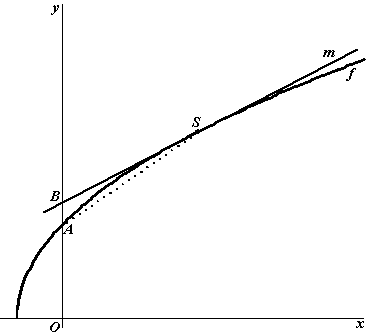



 2
2