OPGAVE 1.
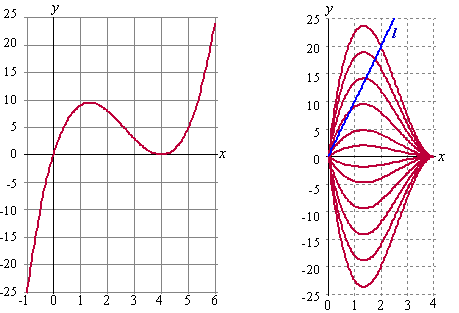
In de figuur hier links onder is de grafiek getekend van  f(x) = x • (x - 4)2  voor  -1 ≤ x ≤ 6. N.B. De schaalverdelingen op de beide assen zijn verschillend.
Tussen x = 0 en x = 4 bereikt de grafiek van f een maximale hoogte.
	1.	Bereken deze hoogte.
De grafiek van f heeft één buigpunt.
	2.	Bereken de coördinaten van dat buigpunt.
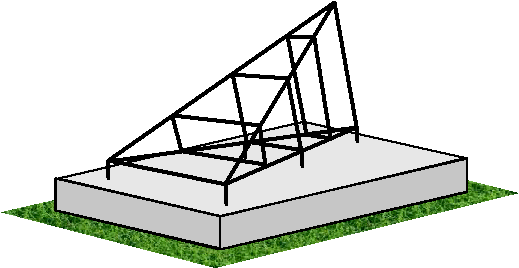
In de figuur rechts boven is de lijn l : y = 10x getekend, en is voor enige waarden van c de grafiek van y = c • f(x) getekend. Voor deze figuur geldt de beperking  0 ≤ x ≤ 4. Eén van de grafieken van y = c • f(x) gaat door het punt P(2, 20)
	3.	Stel een vergelijking op van de raaklijn aan die grafiek in P.
In de figuur rechts hebben sommige grafieken twee punten met l gemeen, andere slechts één punt. Beschouw nu de grafieken van y = c • f(x) voor alle reële waarden van c
	4.	Bereken voor welke waarden van c de grafiek van y = c • f(x) slechts één punt met l gemeen heeft in het gebied  0 ≤ x ≤ 4.

OPGAVE 2.
De basisvorm van het kunstwerk hierboven is een viervlak gemaakt van vier stalen buizen van elk 3 meter en twee stalen buizen van elk 1,5 meter (zie ook de figuur hieronder). In het viervlak zijn twee rechthoeken en één vierkant geconstrueerd. Deze vierhoeken liggen in vlakken parallel met de kortere buizen en verdelen de lange buizen in vier gelijke stukken.
	5.	Bereken hoeveel meter buis er (afgezien van de pootjes) in het kunstwerk is verwerkt.
P en Q zijn de middens van de kortere zijden AB en CD.
	6.	Bewijs dat ribbe AB loodrecht staat op het vlak PCD.
Iemand maakt vanaf het dak van een huis aan de weg een foto van het kunstwerk. Daarbij wordt de camera zó gericht dat de punten P en Q op de foto samenvallen.
	7.	Maak een tekening van het kunstwerk (zonder pootjes) zoals dat op de foto te zien zal zijn. Daarbij mag je net doen of de fotografische weergave tot stand komt via een (loodrechte) parallelprojectie.

OPGAVE 3.
Veranderingen van de waterhoogte in de rivier hebben gevolgen voor de hoogte van het grondwater in het weiland achter de dijk. Het doorgeven van de schommelingen van de waterdruk in de rivier via het grondwater naar het weiland en het opzuigen en weer afstaan van water door het dijlichaam zelf spelen daarbij een rol. Van dit verschijnsel wordt nu een sterk vereenvoudigd wiskundig model gemaakt.
waarbij: HR = waterhoogte rivier in m HW = hoogte grondwater weiland in m t = tijd in maanden.
	8.	Teken in één figuur de grafieken van HR en HW als functie van t voor  0 ≤ t ≤ 12.
	9.	In welk tijdsinterval tussen t = 0 en t = 12 stijgt het water in de rivier terwijl het grondwater in het weiland dan juist aan het dalen is? Licht je antwoord toe.
	10.	Bereken de momenten tussen t = 0  en t = 12 waarop het water in de rivier even hoog staat als het grondwater in het weiland.

OPGAVE 4.
De intensiteit van radioactieve straling neemt af bij het passeren van een absorberende laag. Die afname is afhankelijk van het materiaal en de dikte van de laag en van de intensiteit van de straling.
Als I(x) de intensiteit van de straling is na het passeren van een absorberende laag met een dikte van x (gemeten in mm), dan geldt:  I(x) = I(0) • 2-ax Hierbij is I(0) de intensiteit van de straling voor het passeren van de absorberende laag. In deze opgave houden we de stralingsintensiteit constant. Dat betekent dat de a in bovenstaande formule alleen afhangt van het materiaal van de laag. We noemen a de materiaalconstante bij de gekozen stralingsintensiteit. De halveringsdikte van een zeker materiaal is de dikte van de laag die de intensiteit tot de helft van de oorspronkelijke waarde doet dalen. De halveringsdikte van lood bij de gekozen stralingsintensiteit is 10.
	11.	Bereken de materiaalconstante a van lood.
Voor staal is de halveringsdikte 30. In de figuur hier onder is de intensiteit van de straling na het passeren van een stalen wand met deze halveringsdikte aangegeven door een verticaal lijntje.
	12.	Teken de grafiek van I  als functie van x voor  0 ≤ x ≤ 120.
Voor beton geldt:  I(x) = I(0) • 2-0,02x
	13.	Bereken hoe dik een betonwand moet zijn om de straling tot 1% van de oorspronkelijke waarde te laten afnemen.

OPGAVE 5.
In de punten A, B, C en D van een horizontaal vlak V zijn de loodlijnen a, b, c en d op V opgericht. Door die vier lijnen wordt het lichaam P.EFGH.Q op zijn plaats gehouden. Van dat lichaam ligt het hoekpunt Q in V. Zie de volgende figuur.
Van het lichaam P.EFGH.Q is gegeven:
-	het vlak EFGH is horizontaal
-	EFGH is een vierkant met zijde 6.
-	P en Q liggen beide op afstand 6 van EFGH.
-	in het bovenaanzicht van het lichaam (zie de figuur hier onder) zijn de afstanden EP, PQ en QG gelijk.
Het lichaam wordt gesneden met horizontale vlakken. De positie van zo'n horizontaal vlak (Uh) wordt gegeven door de hoogte h boven het vlak V. De doorsnijdingsfiguur van Uh met het lichaam is een vierkant als 0 < h < 12.
	14.	Teken in het bovenaanzicht de doorsnijdingsfiguren voor h = 2 en voor h = 8.
Voor 0 < h < 12 verdeelt Uh het lichaam in twee delen. We letten verder alleen op het onderste deel. De inhoud I van dat deel varieert met de hoogte h. In de volgende figuur is de grafiek getekend van I als functie van h voor 0 < h < 12.
Bij die grafiek horen twee verschillende formules: één voor 0 < h ≤ 6 en één voor 6 ≤ h < 12.
	15.	Stel die twee formules op.
Bekijk de projectietekening van de beginsituatie bovenaan deze opgave.
	16.	Teken in die figuur de snijlijn van het vlak PFG met V.
Men laat nu het punt Q bewegen in het vlak V. De andere punten van het lichaam P.EFGH.Q blijven op hun oorspronkelijke plaats. Daarbij kan het gebeuren dat Q een zodanige plaats inneemt dat het lichaam in plaats van 8 zijvlakken slechts 7 zijvlakken heeft,  bijvoorbeeld als de driehoeken PFG en QFG in één vlak liggen. Ook kan het zijn dat Q zó ligt dat het lichaam slechts 6 zijvlakken heeft. In de figuur hieronder is een gedeelte van V met de punten A, B, C en D getekend. De loodrechte projectie van P op het vlak V is aangeduid met P'.
	17.	Geef binnen de begrenzing van de figuur duidelijk aan bij welke posities van Q het lichaam respectievelijk 8, 7 of 6 zijvlakken heeft.

UITWERKING
1.	913/27
2.	(22/3, 420/27)
3.	y = -10x + 40
4.	c ≤ 5/8
5.	24 m
6.
7.
8.
9.	9 ≤ t ≤ 10
10.	t = 3,5  en t = 9,5
11.	0,1
12.
13.	332,19 mm
14.
15.	I = 1/3h3  en  I = 144 - 1/3(12 - h)3
16.
17.