HAVO WB12, 2008 - I
Steeds meer vlees

In onderstaande figuur wordt voor de periode 1960 - 1996 zowel de graanproductie als de vleesproductie per hoofd van de wereldbevolking weergegeven. Hiervoor worden twee verticale assen gebruikt. De ronde stippen in de grafiek geven de jaarlijkse graanproductie G per hoofd van de wereldbevolking in kg aan. Het verloop ervan wordt benaderd door een parabool. De driehoekjes geven de jaarlijkse vleesproductie V per hoofd van de wereldbevolking in kg aan. Het verloop ervan wordt benaderd door een rechte lijn (stippellijn).

Volgens de benadering met de rechte lijn in de figuur hierboven was V in 1960 gelijk aan 23,2 kg en in 1996 gelijk aan 36,0 kg. In 1960 werd in Nederland per hoofd van de bevolking 45,3 kg vlees geconsumeerd. Met de gegeven benadering van V is te berekenen wanneer er voor de wereldbevolking per hoofd gemiddeld evenveel vlees geproduceerd zal worden als de Nederlanders in 1960 gebruikten.
5p. 1.

Bereken in welk jaar de wereldvleesproductie volgens de gegeven lineaire benadering 45,3 kg per hoofd van de wereldbevolking zal bedragen.

De parabool in de  figuur kan worden beschreven met de formule G = −0,125t2 + 6,33t + 279 . Hierin is G de wereldgraanproductie per jaar in kg per hoofd van de wereldbevolking en t de tijd in jaren met t = 0 in het jaar 1960.
Volgens de formule heeft G een maximum. Zoals in de figuur is te zien, is dit maximum niet gelijk aan het werkelijke maximum van de jaarlijkse graanproductie per hoofd van de bevolking.
5p. 2.

Bereken met behulp van differentiëren de maximale waarde van G volgens de formule en bepaal met behulp van figuur 1 het verschil tussen dit berekende maximum en de hoogste werkelijke jaarlijkse graanproductie per jaar per hoofd van de bevolking.

Voor de periode 1990 - 2050 gebruiken we nu een andere schatting van de voedselsituatie, die uitgaat van een iets andere formule voor de vleesproductie V in kg per hoofd van de wereldbevolking.
Deze formule wordt gegeven door:  V* = 0,25t + 25 . De tijd t in jaren wordt gerekend vanaf het jaar 1960. Volgens deze formule neemt de vleesproductie steeds verder toe. Dat is alleen mogelijk als men op aarde meer graan gaat gebruiken om aan het vee te voeren, waardoor er minder graan beschikbaar is voor voeding van de mens. Om 1 kg vlees te kunnen produceren is ongeveer 4 kg graan nodig.
5p. 3.

Toon met de gegeven formules voor G en V* aan dat er in het jaar 2000 per hoofd van de wereldbevolking ongeveer 192 kg graan over was voor voeding van de mens.

We gaan ervan uit dat er jaarlijks per hoofd van de wereldbevolking ongeveer 150 kg graan voor voeding van de mens nodig is.
5p. 4.

Bereken met behulp van de bovenstaande formules voor G en V* vanaf welk jaar er door de toenemende vleesproductie te weinig graan over zal zijn voor voeding van de mens.

 

Sterbank.

Op de foto zie je een bank waarvan de zijkanten een regelmatige vijfpuntige stervorm hebben. Deze zijkanten staan verticaal. In deze opgave kijken we niet naar de latten maar naar de meetkundige figuur van de bank zoals die te zien is in figuur 1. Deze meetkundige figuur bestaat uit tien rechthoekige vlakdelen (onder andere de twee vlakken waarop men zit) en twee vlakdelen die de vorm hebben van een vijfpuntige ster. Alle zijden van deze ster zijn 31,0 cm lang.

De vijfpuntige ster bestaat uit een regelmatige vijfhoek ABCDE en vijf gelijkbenige driehoeken. Zie de figuur hiernaast. De punten M, C, B en K liggen op één lijn. De hoeken van de vijfhoek (bijvoorbeeld de hoeken DCB en CDE) zijn allemaal 108º.

 

3p. 5. Bereken ∠DMC

Uit de voorgaande gegevens volgt dat DC ongeveer 19,16 cm is. De breedte van de bank, PL, is 140 cm. Zie de eerste figuur.
4p. 6.

Teken op schaal 1 : 20 het bovenaanzicht van de ondoorzichtige meetkundige figuur van deze bank en geef daarin de hoekpunten L, C, M, D, N en P aan.
5p. 7. Bereken de totale hoogte van de bank.

De bank op de foto is gemaakt van houten latten. Het is ook mogelijk een bank van dezelfde vorm en afmetingen te maken van massief beton. Om te weten hoeveel beton je nodig hebt, kun je de inhoud van de meetkundige figuur berekenen. Daarbij kun je het gegeven gebruiken dat in de vijfpuntige ster de driehoeken ADC en MDC congruent (gelijkvormig en even groot) zijn.
6p. 8.

Bereken met behulp van de meetkundige figuur van de bank hoeveel beton er nodig is. Rond je antwoord af op gehele dm3.

 

Golvend dak.

Op de foto zie je een zwembad met sporthal, samen onder één golvend dak. Het golvende dak bereikt boven het zwembad dezelfde hoogte als boven de sporthal. In de figuur hieronder is een schematisch vooraanzicht getekend. In dit vooraanzicht heeft de rand van het dak de vorm van een sinusoïde met als formule

De hoogte h en de lengte x zijn allebei in meter. De lengte x wordt van links naar rechts over de grond gemeten langs de voorkant van het gebouw, vanaf een punt O dat links van de linkerkant van de voorgevel van het gebouw ligt. Aan beide uiteinden van het gebouw is het dak 8 meter hoog. Zie onderstaande figuur

3p. 9. Bereken exact de minimale en de maximale hoogte van het dak.
4p. 10. Bereken de totale lengte van het gebouw in gehele meters nauwkeurig.

Voordat het zwembad met sporthal werd gebouwd, heeft een architect een ontwerp gemaakt van het gebouw. In het eerste ontwerp dat de architect had gemaakt, was het dak boven het zwembad hoger dan het dak boven de sporthal. Ook de lengte van de voorkant van het gebouw in dit eerste ontwerp was anders dan die van het uiteindelijke gebouw. In de volgende figuur staan de afmetingen van het gebouw volgens het eerste ontwerp.

Het gedeelte van het dak dat boven het zwembad ligt, heeft in het vooraanzicht de vorm van een sinusoïde. Dit geldt ook voor het gedeelte van het dak boven de sporthal. De twee sinusoïdes gaan vloeiend in elkaar over op de grens tussen zwembad en sporthal op een hoogte van 4 meter. Op die grens is de hoogte van het dak minimaal. Boven de sporthal heeft het dak een maximale hoogte van 8 meter. Zie de figuur. Met behulp van deze gegevens kun je een formule opstellen die hoort bij het vooraanzicht van het gedeelte van het dak boven de sporthal volgens het eerste ontwerp
5p. 11. Stel deze formule op. Je mag zelf de oorsprong kiezen. Licht je werkwijze toe.
Horizontale lijnen

In de volgende figuur zie je de grafiek van de functie f die gegeven is door f (x) = 6x − x2 en enkele horizontale lijnen. Deze lijnen horen bij de familie van lijnen y = p met p ≥ 0.

Een van de horizontale lijnen y = p heeft slechts één punt gemeenschappelijk met de grafiek van f.
5p. 12. Bereken op algebraïsche wijze de bijbehorende waarde van p.

In de figuur hieronder zie je dat de grafiek van f door een horizontale lijn y = p gesneden wordt in de punten A en B. Door de punten A en B zie je ook twee verticale lijnen die de x-as snijden in D en C.

De x-coördinaat van A noemen we a, met 0 < a < 3. Voor de oppervlakte S van rechthoek DCBA geldt dan de formule S = (6 − 2a) • (6a − a2)
3p. 13. Leid deze formule af.
Er is één horizontale lijn y = p waarbij de oppervlakte van rechthoek DCBA maximaal is.
6p. 14. Bereken exact de waarde van a in deze situatie.

 

Kegel.

Van een kegel met top T is de diameter van de grondcirkel (AB) 20 cm. Zie de volgende figuur. De afstand van punt T langs de kegelmantel tot de grondcirkel (TA) is 26 cm.

De kegel wordt doorsneden met een vlak evenwijdig aan het grondvlak op hoogte 20 cm. In de figuur is de snijcirkel onder punt T aangegeven. Het gedeelte van de kegel boven het snijvlak is een kleinere kegel met dezelfde top T .
5p. 15.

Bereken de exacte verhouding van de inhouden van de oorspronkelijke kegel en de kleinere kegel.

Voor de oppervlakte O van een kegelmantel geldt de formule: O = πr √(r2+h2).
Hierin is r de straal van de grondcirkel en is h de hoogte van de kegel. Er worden kegels bekeken met hoogten die variëren tussen 10 en 20 cm en met een vaste oppervlakte van de kegelmantel van 300 cm2.
5p. 16.

Bereken welke waarden de diameters van de grondcirkels van deze kegels kunnen aannemen.

 

Combi-functie

De functie f  heeft een voorschrift dat een combinatie is van twee functievoorschriften:

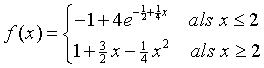
De grafiek van f bestaat dus ook uit twee delen. Deze twee delen sluiten in het punt (2, 3) weliswaar precies op elkaar aan, maar de hellingen van de twee grafiekdelen in dit punt zijn verschillend. Zie bovenstaande figuur.
5p. 17. Bereken met behulp van differentiëren hoe groot die hellingen zijn.

De grafiek uit deze figuur wordt eerst evenwijdig aan de x-as en vervolgens evenwijdig aan de y-as zo verschoven dat de top T van de grafiek in de oorsprong (0, 0) komt te liggen. Bij de nieuwe grafiek die daardoor ontstaat, hoort een andere combinatie van twee functievoorschriften.
5p. 18.

Geef een functievoorschrift dat hoort bij het linkerdeel van de nieuwe grafiek. Licht je werkwijze toe.
UITWERKING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. Een rechte lijn door  (0, 23.2) en (36, 36.0) opstellen.
hellinggetal is a = (36.0 - 23.2)/(36 - 0) = 0,3556
begingetal is  b = 23.2
De lijn is dus  V = 0,3556 • t + 23,2
0,3556 • t + 23,2 = 45,3  ⇒  0,3556t = 22,1  ⇒  t = 62,16 en dat is in 2022
2. G'= -2 • 0,125t + 6,33 = -0,25t + 6,33 = 0  ⇒  0,25t = 6,33 ⇒  t = 25,32
Invullen geeft  G(25,32) = -0,125 • 25,322 + 6,33 • 25,32 + 279 = 359,1378 ≈ 359 kilo

Aflezen geeft een maximale G van ongeveer 378 kilo

Dat scheelt  378 - 359 = 19 kilo.
3. 2000 is  t = 40
V* = 0,25 • 40 + 25 = 35 en voor de productie daarvan is  4 • 35 = 140 kg graan nodig.
G(40) = -0,125 • 402 + 6,33 • 40 + 279 = 332,2
Er blijft dus over 332,2 - 140 = 192,2 en dat is inderdaad ongeveer 192 kg.
4. Voor V*  kilo vlees is  4 • V* kilo graan nodig.
Als er G kilo graan is, dan blijft er dus nog  G - 4 • V* kilo over.
Dat moet gelijk zijn aan 150:  G - 4 • V* = 150
Invullen:  -0,125t2 + 6,33t + 279 - 4 • (0,25t + 25) = 150
Het kan natuurlijk via Intersect van de rekenmachine, maar algebraïsch is veel leuker:

-0,125t2 + 6,33t + 279 - t + 100 = 150
⇒  -0,125t2 + 5,33t + 29 = 0
ABC formule met a = -0,125 en b = 5,33 en c = 29 geeft  t = -4,88   ∨  t = 47,52
De laatste is het goede antwoord, en dat is in 1960 + 47,52 = 2007.
5. ∠DCB = 108º dus  ∠DCM = 180 - 108 = 72º
Dan is ∠CDM ook 72º
∠DMC = 180 - 72 - 72 = 36º
6.
7. Het is de hoogte van driehoek OMK. Noem die hoogte h.
∠MOK = ∠MDC = 72º
MO = 31,0 + 19,16 + 31,0 = 81,16
sin(∠MOK) = sin(72º) = h/MO = h/81,16
Daaruit volgt h = 81,16 • sin(72º) ≈ 77,19 cm
8. Inhoud = oppervlakte ster • 140.
De ster bestaat uit 6 blauwe en 2 oranje driehoeken zoals hiernaast.

blauwe driehoek:
hoogte h: sin72 = h/31,0 
⇒  h = 31,0 • sin72
basis b:  cos72 = 0,5b/31,0
⇒  b = 31,0 • cos72/0,5 = 62 • cos72
(dat was de 19,18 trouwens)
oppervlakte is  0,5 • (62 • cos 72) • (31,0 • sin72)

oranje driehoek:
hoogte h:  tan36 = h/15,5
⇒  h = 15,5 • tan36
oppervlakte is  0,5 • 31,0 • 15,5 • tan36
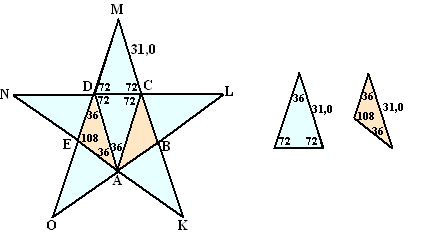De totale oppervlakte is dan:
6 • 0,5 • (62 • cos 72) • (31,0 • sin72) + 2 • 0,5 • 31,0 • 15,5 • tan36 ≈ 2043,6886
Het hele lichaam heeft dan inhoud  140 • 2043,6886 ≈ 286116 dm3 
9. Een sinus is maximaal 1 en minimaal -1
De hoogte is dan maximaal  3 • 1 + 7 = 10m  en  minimaal  3 • -1 + 7 = 4 m.
10. Plot de grafiek  Y1 = 3*sin(π*X/30) + 7  en de lijn Y2 = 8
Denk erom dat je rekenmachine op radialen staat  (MODE - Radian).
window bijv. Xmin = 0, Xmax = 100, Ymin = 0, Ymax = 12
intersect met de juiste twee snijpunten geeft  X ≈ 3,245 en X ≈ 86,755
De lengte daartussen is ongeveer 86,755 - 3,245 ≈ 84 m.
11. Het maximum is 8 en het minimum is 4, dus de evenwichtslijn is  y = 6 en de amplitude is 2.
De afstand tussen het beginpunt met hoogte 4 en het eindpunt met hoogte 6 is 3/4 periode en dat is 48m
Een periode is dus 64 m.
Kies als oorsprong bijvoorbeeld het punt waar de hoogte 6 meter is (16 meter naast het begin van de sporthalgrafiek)
Dan wordt de formule:  y = 6 + 2 • sin(2π/64 • x)
12. het snijpunt moet dan de top zijn.
De top van y = 6x - x2  ligt bij x = 3  (door xTOP = -b/2a   of   door y' = 6 - 2x = 0 te vinden)
Als x = 3 dan is y = 6 • 3 - 32 = 9
Het is dus de lijn  y = 9, dus p = 9.
13. DC = CO - OD = (6- a) - a = 6 - 2a
AD is de y-coördinaat die hoort bij x = a en dat is  6a - a2
Oppervlakte = DC • AD = (6 - 2a) • (6a - a2) en dat is inderdaad de gegeven formule.
14. In het maximum van S geldt  S'= 0
S = 36a - 6a2 - 12a2 + 2a3 = 36a - 18a2 + 2a3
S' = 36 - 2 • 18a + 3 • 2a2 = 36 - 36a + 6a2 = 0
De ABC formule met a = 6 en b = -36 en c = 36 geeft   a = 3 ± √3 en dat geeft  4,73  of  1,27
De juiste oplossing is dus a = 3 - √3 ≈ 1,27
15. De hoogte van de oorspronkelijke kegel vind je door Pythagoras in driehoek TMA (M midden van AB):
h2 + 102 = 262  ⇒  h = 24
De hoogte van het bovenste kegeltje is dan 24 - 20 = 4
De vergrotingsfactor k is dan gelijk aan 24/4 = 6
Voor de inhoud is de verhouding dan k3 = 63 = 216.
De kegelinhouden verhouden zich dus als 1 : 216.
16. h = 10 geeft  300 = πr • √(r2 + 100)
Y1 = 300 en Y2 = πX*√(X^2 + 100) en dan intersect geeft  X = 7,60

h = 20 geeft  300 = πr • √(r2 + 400)
Y1 = 300 en Y2 = πX*√(X^2 + 400) en dan intersect geeft  X = 4,65

De diameter is tweemaal de straal dus dat varieert tussen 9,3 en 15,2

17. x ≤ 2:  f '= 4 • e(-0,5 + 0,25x) • 0,25  (die 0,25 komt van de kettingregel) en  f '(2) = 1
x ≥ 2:  f ' = 3/2 - 1/2x  en  f '(2) = 1/2 
18. Bereken eerst de top:
f '= 0 geeft  3/2 - 1/2x = 0  en dus  x = 3, en y = 1 + 3.2 • 3 - 1/4 • 32 = 31/4.
De grafiek moet dus 3 naar links geschoven worden en 31/4 omlaag.
Dan moet x worden vervangen door (x + 3) en bovendien moet er -31/4 achter de hele formule gezet worden.
Dat geeft: y = -1 + 4e(-0,5 + 0,24(x + 3)) - 31/4