HAVO WB12, 2007 - I

 

De Wet van Moore
Eén van de belangrijkste onderdelen van de computer is de chip. Een chip is een elektronische schakeling die uit vele duizenden transistors bestaat. Toch is een chip niet groter dan een paar vierkante millimeter.
In 1961 maakte men de eerste experimentele chip, bestaande uit 4 transistors. Gordon Moore was één van de mensen die bij het ontwerp van de chip betrokken waren In 1965 voorspelde hij dat het aantal transistors per chip exponentieel zou gaan groeien. Deze voorspelling werd bekend als de "Wet van Moore".

Tot nu toe is gebleken dat er per 2 jaar ongeveer een verdubbeling van het aantal transistors op een chip plaatsvindt. De formule voor de Wet van Moore die hierbij hoort is:

Hierin is A het aantal transistors op één chip en t het aantal jaren vanaf 1961.
3p 1. Bereken uit hoeveel transistors één chip in 1975 volgens deze formule bestond.

 
In 1968 was Moore één van de oprichters van het bedrijf Intel dat vooral bekend werd door een speciaal soort chip: de processor. De eerste Intel-processor werd gemaakt in 1971. Hij bestond uit ongeveer 2250 transistors.
Men neemt aan dat het aantal transistors van één processor ook elke twee jaar verdubbelt. De formule die hierbij hoort is:

Hierin is P het aantal transistors van de processor en t het aantal jaren vanaf 1971.

Veronderstel dat, tegen de verwachting van de huidige wetenschappers in, de formules voor A (het aantal transistors per chip) en P (het aantal transistors per processor) onbeperkt blijven gelden.
 
6p 2. Bereken het aantal jaren verschil tussen de momenten waarop A en P de grens van 1 miljard (109) overschrijden.

 
In onderstaande figuur zie je vanaf 1971 de jaren en de aantallen transistors van de verschillende processors die Intel gemaakt heeft tot het jaar 2003, bijvoorbeeld de 4004-processor, de 8008 processor en de Pentium-processors.
Merk op dat de stapgrootte op de verticale as steeds groeit met een factor 10. Men heeft de logaritme van het aantal transistors uitgezet tegen het jaar waarin de processor werd gemaakt. op de schaalverdeling staan echter wel de oorspronkelijke aantallen weergegeven.

De blauwe lijn in deze figuur hoort bij de eerder genoemde formule voor P.
Deze lijn begint met de 2250 transistors van de 4004-processor. Bij deze rechte lijn hoort een formule van de vorm  log(P) = a • t + b. Je kunt deze formule vinden door uit te gaan van de formule P = 2250 • 20,5t
4p 3. Bereken de waarden van a en b door de laatste formule te herleiden. Rond af op twee decimalen.

 
Wortelfuncties
Een functie f is gegeven door:  f(x) = √(x2 + 9)
In de figuur is de grafiek van f afgebeeld.

De lijn k met vergelijking  y = 4 snijdt de grafiek van f in de punten A en B.

4p 4. Bereken de exacte lengte van lijnstuk AB.

 
Vervolgens bekijken we de functie g die gegeven is door g(x) = 5 - √(x2 + 9).

De grafiek van g kan door twee achtereenvolgende transformaties ontstaan uit de grafiek van f.
4p 5. Geef aan welke twee transformaties op de grafiek van f kunnen worden toegepast, en in welke volgorde, om de grafiek van g te laten ontstaan.

 
De grafiek van g snijdt de negatieve x-as in het punt P met xP = -4.
De raaklijn in P aan de grafiek van g snijdt de y-as in het punt S
5p 6. Bereken met behulp van differentiëren de coördinaten van het punt S.

 

 

Afgeknotte piramide
Van een afgeknotte piramide ABCD.EFGH zijn het grondvlak en het bovenvlak vierkanten.Het grondvlak heeft zijden van 8 cm en het bovenvlak heeft zijden van 3 cm. De ribbe CG staat loodrecht op het grondvlak en heeft een lengte van 6 cm. Zie de figuur hiernaast.

4p 7. Bereken de hoek die AE met het grondvlak ABCD maakt.

 
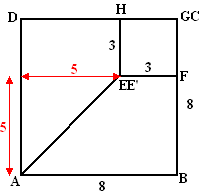
Hieronder is op schaal  1 : 2 een begin gemaakt van een uitslag van deze afgeknotte piramide.

5p 8. Maak deze uitslag af. Zet alle letters er op de juiste plek bij.
Egyptische wiskundigen hebben zich in de oudheid al bezig gehouden met inhoudsformules van piramides en afgeknotte piramides. Voor de inhoud van een afgeknotte piramide met vierkant grondvlak en bovenvlak vonden zij de volgende formule:

Hierin is:
a de lengte van de zijde van het grondvlak
b de lengte van de zijde van het bovenvlak
h de hoogte van de afgeknotte piramide.
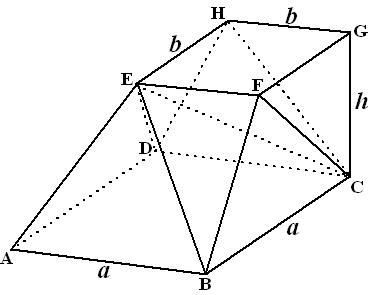
Voor de volgende vraag bekijken we zo'n afgeknotte piramide ABCD.EFGH waarvan de ribbe CG loodrecht op het grondvlak staat. Zie de figuur hiernaast.
ABCD is een vierkant met zijde a  en EFGH is een vierkant met zijde b.
De afgeknotte piramide is opgedeeld in de volgende vier piramides: 
E.ABCD,  C.EFGH,  E.BCF en E.HDC
5p 9. Leid de formule van de Egyptenaren af met behulp van de inhoud van deze vier piramides.

 

 

Mobiele Telefoon
Een mobiele telefoon werkt op een batterij. Zo'n telefoon kan vrij lang aanstaan als je niet belt. De maximale tijd dat de mobiele telefoon aan kan staan zonder gebruikt te worden heet de stand-by tijd. Als je wel belt, verbruikt de telefoon meer energie. De batterij is dan sneller leeg.

Bij een telefoon op stand-by stand met een moderne batterij wordt het spanningsverloop benaderd door de formule:

Hierin is V  de spanning van de batterij in Volt en t de tijd in uur.
Op tijdstip t = 0 is de batterij vol.

De telefoon staat vanaf het ogenblik waarop de batterij net helemaal is opgeladen stand-by totdat de spanning tot 0 is gedaald. in minuten nauwkeurig is deze stand-by-tijd gelijk aan 141 uur en 39 minuten.  
3p 10. Laat dit met een berekening zien.

 
De spanning die de batterij levert kun je aan de rechterkant van het scherm aflezen. Daar zijn vier blokjes die aan of uit kunnen staan. Als de batterij vol is, staan alle blokjes (nummers 1 t/m 4) aan.
Bij een volle batterij bedraagt de spanning ongeveer 3,2 Volt.
Het aantal blokjes dat 'aan' staat wordt bepaald door het percentage van de maximale spanning. Als het percentage minder dan 75% bedraagt kan er niet meer getelefoneerd worden en zijn alle blokjes uit. Zie onderstaande tabel.
blokjes die zichtbaar zijn percentage van de
maximale spanning
1,2,3,4 100 - 97
2,3,4 97 - 94
3,4 94 - 88
4 88 - 75
geen 75 - 0
Iemand laadt de batterij helemaal op. Vervolgens legt hij de telefoon in de stand-by stand weg. De telefoon wordt niet gebruikt. Na verloop van tijd gaat blokje nummer 1 uit. Een tijd nadat blokje nummer 1 is uitgegaan, gaat blokje nummer 2 uit. Juist op dat moment pakt hij de telefoon, ziet blokje nummer 2 uitgaan en denkt dat de telefoon op de helft van zijn stand-by tijd is. Er zijn dan immers nog twee blokjes (nummer 3 en 4) van de vier zichtbaar
5p 11. Onderzoek met behulp van de gegeven formule of de telefoon op het moment dat blokje nummer 2 uitgaat, op de helft van zijn stand-by tijd is.

 
Bij een ouderwetse batterij neemt de spanning als de telefoon stand-by staat lineair met de tijd af volgens de formule  V = -0,01t + 3,2
In deze formule is V de spanning van de batterij in Volt en t de tijd in uur.

Als de telefoon stand-by staat, ontlaadt de ouderwetse batterij de hele tijd met dezelfde snelheid. Bij de moderne batterij hangt deze snelheid van ontladen af van het moment. De formule die het spanningsverloop benadert van een moderne batterij die stand-by staat, kan ook geschreven worden als:
V = 3,31 + 21 • (t - 148)-1

5p 12. Bereken met behulp van differentiëren het tijdstip waarop de moderne batterij even snel ontlaadt als de oude als de telefoon stand-by staat. Rond het antwoord af op hele uren.

 

 

Klimtoestel.
Op de foto zie je een klimtoestel bij basisschool 'De Grundel' in Lelystad. Dit toestel is opgebouwd uit 16 buizen en 9 metalen bollen. In het verdere verloop van deze opgave worden de bollen als punten voorgesteld en de buizen als rechte lijnstukken.


In de figuur hier linksonder is het klimtoestel in een denkbeeldige kubus geplaatst met grondvlak ABCD.
De punten E, F, G en H zijn snijpunten van de zijvlaksdiagonalen.
T is het snijpunt van de diagonalen in het bovenvlak.
In de figuur rechtsonder is een bovenaanzicht (verkleind) van het klimtoestel weergegeven.

4p 13. Hieronder is lijn AB getekend in een aanzicht van het toestel waarbij de kijkrichting evenwijdig is aan EG. Maak dit aanzicht af. Zet alle letters er op de juiste plek bij.

 

Elke buis in het klimtoestel is 3 m lang.
4p. 14. Laat met een berekening zien dat de hoogte van het klimtoestel ongeveer 4,24 m is.

 
Sommige buizen van het klimtoestel zijn evenwijdig met buis HT, andere snijden HT en er zijn buizen die HT kruisen.
3p 15. Noem alle buizen die buis HT kruisen.
Het klimtoestel wordt met behulp van driehoekige platen die aan de buizen worden bevestigd, omgebouwd tot een speelhuisje. De hoogte van het huisje is ongeveer 4,24 meter.
5p 16. Bereken de inhoud van het speelhuisje T.AFGH.ABCD. Geef je antwoord in gehele m3 .

 

 

Wandelende duinen.
Bij de stad Laâyoune in Zuid-Marokko bevindt zich in de woestijn een duingebied. De duinen hebben van bovenaf gezien de vorm van een halve maan. Zo'n halve maan ontstaat als de windrichting het hele jaar constant is en er niet voldoende zand aanwezig is voor de vorming van complete duinen. Zie de foto hieronder.

Wetenschappers hebben van zo'n duin de afmetingen precies opgemeten. Met hun metingen maakten zij de tekening hier linksboven.

In de figuur rechtsboven is een dwarsdoorsnede langs de lijn AB getekend van het zelfde duin. Langs de horizontale as is de afstand x tot het midden uitgezet en langs de verticale as de hoogte h van het duin. Links van het midden (richting A) wordt de afstand x negatief gerekend.
De vorm van deze doorsnede van het duin wordt benaderd met een deel van een cosinuskromme. Het hoogste punt van het duin, T (boven het snijpunt van  lijn AB en lijn CD), is ongeveer 6,37 meter hoog. Bij benadering geldt nu:  h = 6,37 • cos(b • x)  met h en x in meter.
4p 17. Bereken met behulp van de figuur rechtsboven de waarde van b in deze formule. Rond af op drie decimalen.

 
De doorsnede van het duin langs lijn CD is hieronder getekend.

In deze opgave benaderen we de doorsnede met een eenvoudig model. Hierin is h de hoogte in meter en is x de afstand in meter langs de lijn CD gemeten vanaf punt C.

De doorsnede in de figuur hierboven bestaat uit twee delen. Voor het linker gebogen deel gebruiken we een deel van een cosinusgrafiek. De formule die hierbij hoort wordt gegeven door:

Het rechterdeel na de top van het duin, dat ligt tussen de punten (41; 6,37) en (52; 0), benaderen we met het lijnstuk dat die punten verbindt. De formule die hierbij hoort is van de vorm h(x) = ax + b.
Door berekening blijkt dat a ≈ -0,58 en b ≈ 30,11
4p 18. Toon dit met een berekening aan.

 
De windrichting (van C naar D) is bijna het hele jaar door gelijk en is in de figuur aan het begin van deze opgave aangegeven door de richting van de pijl. Door de wind verplaatsen de duinen zich, waarbij de vorm vrijwel gelijk blijft. Bij het duin hierboven gebeurt dat met een snelheid van 65 meter per jaar.

Midden op het pad van het 'wandelende duin' staat een paal van 2 meter hoog. Het duin zal over de paal heen gaan, waardoor de paal gedurende een tijd onder het zand verborgen zal zijn. Zie de figuren hiernaast.

7p 19. Bereken met behulp van de formules voor h(x) hoe lang de paal onder het zand zal zijn verdwenen. Rond je antwoord af op hele maanden.

 

 
UITWERKINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. In 1975 is t = 14, en  4 • 20,5 • 14 = 4 • 27 = 4 • 128 = 512.
   
2. A = 109    geeft  109 = 4 • 20,5t  en dat levert met intersect  t = 55,8 en dat is in 2016
P = 109  geeft  109 = 2250 • 20,5t  en dat levert met intersect  t = 37,5 en dat is in 2008
Het verschil is 8 jaar
3. log(P) = log(2250 • 20,5t) = log(2250) + log(20,5t) = log(2250) + 0,5t • log(2) = 0,5•log(2) • t + log(2250)
dus a = 0,5 • log(2) ≈ 0,15 en  b = log(2250) ≈ 3,35
4. √(x2 + 9) = 4  ⇒  x2 + 9 = 16  ⇒  x2 = 7  ⇒  x = √7  of  x = -√7
De afstand daartussen is AB = 2√7. 
5. Er is eerst een minteken voor de formule gekomen en er is daarna 5 bij opgeteld.
minteken:  spiegelen in de x-as
5 erbij op:  5 omhoog schuiven (translatie)
6. g(x) = 5 - (x2 + 9)0,5 
g' (x) = -0,5 • (x2 + 9)-0,5 • 2x  (laatste stukje vanwege de kettingregel)
g'(-4) = -0,5 • ((-4)2 + 9)-0,5 • 2 • -4 = 0,8 en dat is het hellinggetal van de raaklijn.
De raaklijn is dus van de vorm  y = 0,8x + b en moet door (-4, 0) gaan
0 = 0,8 • -4 + b  geeft  b = 3,2
De raaklijn is dus  y = 0,8x + 3,2
Die snijdt de y-as als x = 0:  y = 0,8 • 0 + 3,2 = 3,2, dus  S = (0, 3.2)
7. Het is hoek EAE' waarbij E' de projectie van E op het grondvlak is. 
E' ligt op AC.
In het bovenaanzicht hiernaast zie je dat AE' 2 = 52 + 52 
dus AE'= √50
In driehoek EAE' :  tan(EAE') = 6/√50
Daaruit volgt  EAE' ≈ 40,3º
8.

9. E.ABCD:  hoogte h, grondvlak a2  dus inhoud  1/3 • a2 h
C.EFGH:  hoogte h, grondvlak b2  dus inhoud  1/3 • b2 h
E.BCF:  hoogte EF = b, grondvlak BCF =  1/2 • ah  dus inhoud  1/6 • abh
E.HDC:  hoogte EH = b,  grondvlak HDC = 1/2 • ah  dus inhoud  1/6 • abh
Samen wordt dat  1/3 • a2 h + 1/3 • b2 h + 1/6 • abh + 1/6 • abh
Neem de laatste twee termen samen en je hebt de gevraagde formule.
10. 141 uur en 39 minuten is  14139/60 uur = 141,65 uur.
3,31 + 21/(141,65 - 148) = 3,31 - 3,30708  ≈ 0

of:
0 = 3,31 + 21/(t - 148) ⇒  -3,31 = 21/(t - 148)  ⇒  -3,31(t - 148) = 21  ⇒  -3,31t + 489,88 = 21
⇒ -3,31t = -468,88  ⇒  t  = 141,6555.. uur = 141 + 0,6555... uur
0,6555 uur is  0,6555 • 60 = 39,3 minuten.
11. Op dat moment is het percentage 94, dus de spanning  0,94 • 3,2 = 3,008
3,008 = 3,31 + 21/(t - 148)
GR:  Y1 = 3,008  en  Y2 = 3,31 + 21 : (X - 148)
window bijv.  Xmin = 0,   Xmax = 200,  Ymin = 0,  Ymax = 6
intersect geeft  t = 78,46
De helft van de stand-by tijd is  0,5 • 141,65 = 70,825.
De telefoon is op dat moment dus niet op de helft van zijn stand-by tijd.
12. De oude ontlaadt met een snelheid van  0,01 (V/uur)
De nieuwe ontlaadt even snel als de afgeleide gelijk is aan -0,01
V'(t) = -1 • 21 • (t - 148)-2  = -0,01
Intersect met de GR geeft  t ≈ 102 uur
13.

14. E was snijpunt van de zijvlaksdiagonalen van de kubus, dus E ligt op de halve hoogte van het hele toestel.
Teken de projectie E' van E op AB, dan geldt Pythagoras in driehoek EAE' .
Stel EE'= AE'= x, dan geldt  x2 + x2 = 32  ⇒  2x2 = 9  ⇒  x2 = 4,5  ⇒  x = √4,5
De hoogte is dus 2 • √4,5 ≈ 4,24
15. GF, EF, AE, DG, GC, BE
16. Snij het huisje halverwege horizontaal in twee delen.
Het bovenste deel is piramide T. HEFG met inhoud 1/3 • 2,12 • 32 ≈ 6,36

Het onderste deel is een halve kubus waar vier piramides uit zijn weggehaald.
Zo'n piramide heeft inhoud  1/3 • ( 1/2 • 2,12 • 2,12)  • 2,12 ≈ 1,59
het overblijvende deel heeft dan inhoud  1/2 • 4,243 - 4 • 1,59 ≈ 31,75

Samen is de inhoud dan  6,36 + 31,75 ≈ 38 m3

Sneller:  Als je piramide T.HEFG in 4 gelijke delen snijdt (diagonalen in HEFG) dan passen die delen precies naast het speelhuisje in de onderste helft van de kubus.
De inhoud van het huisje is daarom gelijk aan de halve kubus: 0,5 • 4,243 ≈ 38.
17. De periode van de cosinusgrafiek is  2π/b
Uit de figuur zie je dat de halve periode ongeveer gelijk is aan 70, dus de periode 140
2π/b = 140  als  b = 2π/140  ≈  0,045
18. a = Δy/Δx = (6,37 - 0)/(41 - 52) = 6,37/-11 ≈ -0,579
de vergelijking is dan h = -0,579x + b en die moet door bijv.  (52,0) gaan
dus  0 = -0,579 • 52 + b  = -30,11  ⇒  b ≈ 30,11
19. Y1 = -0,58x + 30,11
Y2 = 3,25 - 3,25cos(π/45 • x)   (rekenmachine op radialen!)
Y3 = 2
Gebruik intersect (Y1 met Y3  en  Y2 met Y3)
window bijv.  Xmin = 0,  Xmax = 60,  Ymin = 0,   Ymax = 4
Dat geeft  X = 48,4655... en X = 16,845...
De afstand daartussen is ongeveer  31,62 m  dus dat kost  31,62/65 = 0,486 jaar
Dat is  0,486 • 12 = 6 maanden